Giải bài tập 9 trang 47 SGK Toán 12 tập 1 - Cánh diều — Không quảng cáo

Đề bài

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau

a,$y = {x^3} - 3{x^2} + 2$

$b,\;y =  - {x^3} + 3{x^2} - 6x$

$c,y = \frac{{3x - 2}}{{x - 2}}$

$d,y = \frac{x}{{2x + 3}}$

$e,y = \frac{{{x^2} + 2x + 4}}{x}$

$g,y = \frac{{{x^2} + 4x + 3}}{{x + 2}}\;$

Lời giải chi tiết

$a,\;y = {x^3} - 3{x^2} + 2$

TXD : R

$y' = 3{x^2} - 6x$

Cho y= 0 => $\left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.$

Bảng biến thiên:

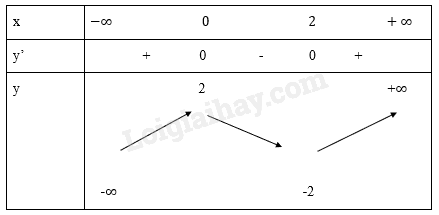
Đồ thị hàm số:

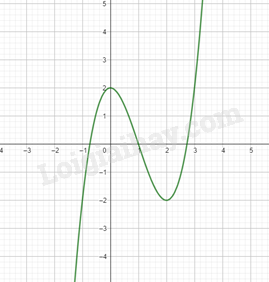
Hàm số đồng biến trong khoảng $\left( { - \infty ;0} \right)$ và $\left( {2; + \infty } \right)$

Hàm số nghịch biến trong khoảng (0;2)

$\;b,\;y =  - {x^3} + 3{x^2} - 6x$

TXD: R

$y' = \; - 3{x^2} + 6x - 6$

Bảng biến thiên:

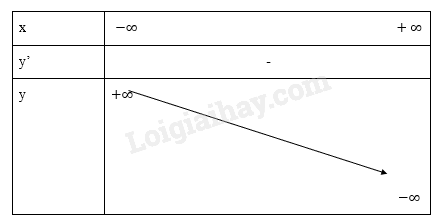
Đồ thị hàm số

Hàm số nghịch biến trên R

$c,y = \frac{{3x - 2}}{{x - 2}}$

TXD: R/2

$\mathop {\lim }\limits_{x \to  + \infty } \frac{{3x - 2}}{{x - 2}} = 3 =  > TCN\;y = 3$

$\mathop {\lim }\limits_{x \to {2^ - }} \frac{{3x - 2}}{{x - 2}} =  - \infty$

Bảng biến thiên:

Đồ thị hàm số:

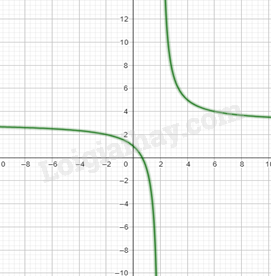
Hàm số nghịch biến trên khoảng R

$d,y = \frac{x}{{2x + 3}}$

TXD: R \ {$- \frac{3}{2}$}

TCN $y = \frac{1}{2}$

TCD $x =  - \frac{3}{2}$

Bảng biến thiên

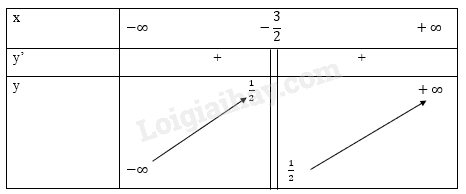
Đồ thị hàm số:

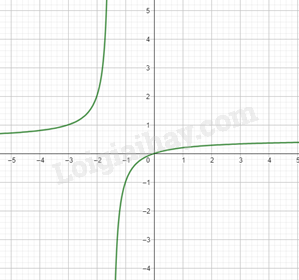
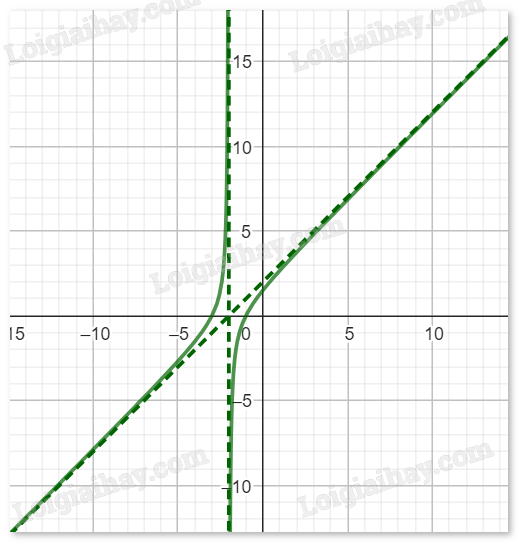
$e,y = \frac{{{x^2} + 2x + 4}}{x}$

$TXD:\mathbb{R}\backslash \{ 0\}$

TCD: x = 0.

Không có tiệm cận ngang.

Có thể viết hàm số đã cho dưới dạng: $y = \frac{{{x^2} + 4x + 3}}{{x + 2}} = x + 2 + \frac{4}{x}$, suy ra:

$\begin{array}{l}\mathop {\lim }\limits_{x \to  + \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to  + \infty } \frac{4}{x} = 0.\\\mathop {\lim }\limits_{x \to  - \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to  - \infty } \frac{4}{x} = 0.\end{array}$

Do đó, đồ thị hàm số có $y = x + 2$ là tiệm cận xiên.

$y' = \frac{{\left( {2x + 2} \right)x - \left( {{x^2} + 2x + 4} \right)}}{{{x^2}}} = \frac{{{x^2} - 4}}{{{x^2}}}$.

Cho y’=0 => x=$\pm 2$.

Bảng biến thiên:

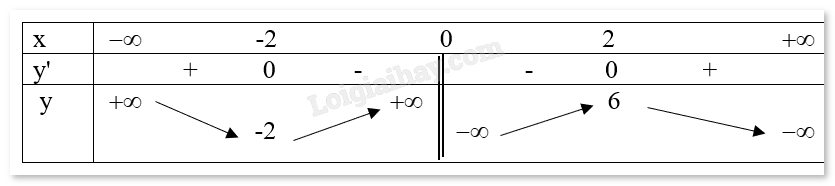
Đồ thị hàm số:

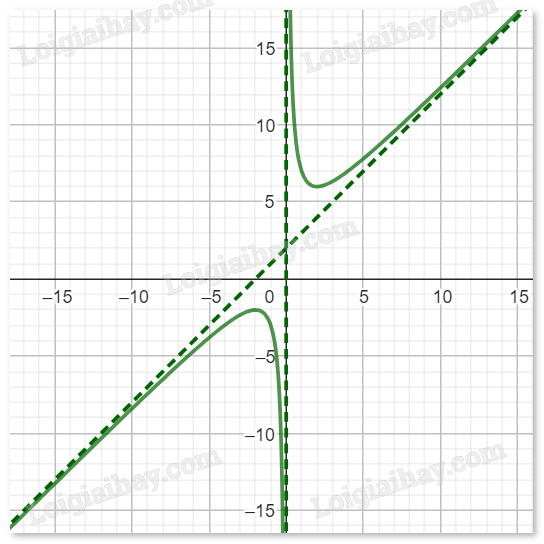
g, $y = \frac{{{x^2} + 4x + 3}}{{x + 2}}$

TXD: $\mathbb{R}\backslash \{  - 2\}$.      

$\mathop {\lim }\limits_{x \to  + \infty } y =  + \infty ,\mathop {\lim }\limits_{x \to  - \infty } y =  - \infty$. Đồ thị àm số không có tiệm cận ngang.

$\mathop {\lim }\limits_{x \to  - {2^ + }} y =  - \infty ,\mathop {\lim }\limits_{x \to  - {2^ - }} y =  + \infty$. Đồ thị hàm số có $x =  - 2$ là tiệm cận đứng.

Có thể viết hàm số đã cho dưới dạng: $y = \frac{{{x^2} + 4x + 3}}{{x + 2}} = x + 2 - \frac{1}{{x + 2}}$, suy ra:

$\begin{array}{l}\mathop {\lim }\limits_{x \to  + \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to  + \infty } \frac{{ - 1}}{{x + 2}} = 0.\\\mathop {\lim }\limits_{x \to  - \infty } \left[ {y - (x + 2)} \right] = \mathop {\lim }\limits_{x \to  - \infty } \frac{{ - 1}}{{x + 2}} = 0.\end{array}$

Do đó, đồ thị hàm số có $y = x + 2$ là tiệm cận xiên.

Bảng biến thiên:

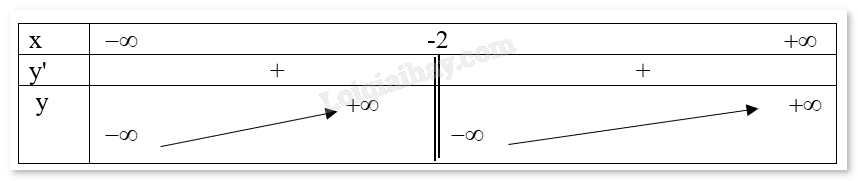
Đồ thị hàm số: