Giải mục 2 trang 39, 40 SGK Toán 11 tập 2 - Chân trời sáng tạo — Không quảng cáo

Hoạt động 2

Cho hàm số $y = f\left( x \right) = \frac{1}{2}{x^2}$ có đồ thị $\left( C \right)$ và điểm $M\left( {1;\frac{1}{2}} \right)$ thuộc $\left( C \right)$.

a) Vẽ $\left( C \right)$ và tính $f'\left( 1 \right)$.

b) Vẽ đường thẳng $d$ đi qua điểm $M$ và có hệ số góc bằng $f'\left( 1 \right)$. Nêu nhận xét về vị trí tương đối giữa $d$ và $\left( C \right)$.

Phương pháp giải:

a) Tính giới hạn $f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}$.

b) Phương trình đường thẳng đi qua điểm $A\left( {{x_0};{y_0}} \right)$ có hệ số góc $k$ là: $y - {y_0} = k\left( {x - {x_0}} \right)$.

Lời giải chi tiết:

a)

$\begin{array}{l}f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}{x^2} - \frac{1}{2}}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}\left( {{x^2} - 1} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}\left( {x - 1} \right)\left( {x + 1} \right)}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{1}{2}\left( {x + 1} \right) = \frac{1}{2}\left( {1 + 1} \right) = 1\end{array}$

b) Phương trình đường thẳng $d$ đi qua điểm $M\left( {1;\frac{1}{2}} \right)$ và có hệ số góc bằng $k = f'\left( 1 \right) = 1$ là: $y - \frac{1}{2} = 1\left( {x - 1} \right) \Leftrightarrow y = x - 1 + \frac{1}{2} \Leftrightarrow y = x - \frac{1}{2}$.

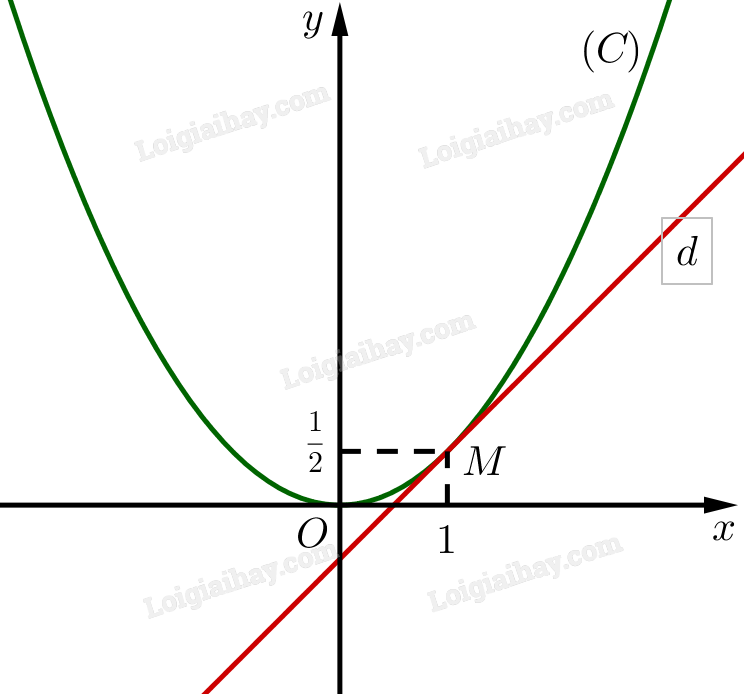
Đường thẳng $d$ cắt đồ thị hàm số $\left( C \right)$ tại duy nhất điểm $M\left( {1;\frac{1}{2}} \right)$.

Thực hành 2

Cho $\left( C \right)$ là đồ thị của hàm số $f\left( x \right) = \frac{1}{x}$ và điểm $M\left( {1;1} \right) \in \left( C \right)$. Tính hệ số góc của tiếp tuyến của $\left( C \right)$ tại điểm $M$ và viết phương trình tiếp tuyến đó.

Phương pháp giải:

Hệ số góc: $f'\left( {{x_0}} \right)$.

Phương trình tiếp tuyến: $y - f\left( {{x_0}} \right) = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)$.

Lời giải chi tiết:

Ta có: ${\left( {\frac{1}{x}} \right)^\prime } =  - \frac{1}{{{x^2}}}$ nên tiếp tuyến của $\left( C \right)$ tại điểm $M$ có hệ số góc là: $f'\left( 1 \right) =  - \frac{1}{{{1^2}}} = 1$

Phương trình tiếp tuyến của $\left( C \right)$ tại điểm $M$ là: $y - 1 = 1\left( {x - 1} \right) \Leftrightarrow y = x$.