Giải mục 2 trang 76 SGK Toán 9 tập 2 - Cánh diều
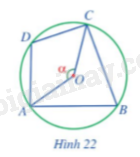
Trong Hình 22, cho biết (widehat {AOC} = a.) Tính số đo của các cung và góc sau theo a. a) (oversetfrown{ADC},widehat{ABC;}) b) (oversetfrown{ADC},widehat{ABC;}) c) (widehat{ADC}+widehat{ABC.})
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 76 SGK Toán 9 Cánh diều
Trong Hình 22, cho biết \(\widehat {AOC} = \alpha.\)
Tính số đo của các cung và góc sau theo \( \alpha\).
a) \(\overset\frown{ADC},\widehat{ABC;}\)
b) \(\overset\frown{ADC},\widehat{ABC;}\)
c) \(\widehat{ADC}+\widehat{ABC.}\)
Phương pháp giải:
Lý thuyết: Trong một đường tròn, số đo góc ở tâm bằng số đo cung bị chắn, số đo góc nội tiếp bằng nửa số đo cung bị chắn.
Lời giải chi tiết:
a) Xét (O) có \(\widehat {AOC}\) là góc ở tâm chắn cung CDA nên \(\widehat {AOC}\)= sđ\(\overset\frown{CDA}= \alpha.\)
\(\widehat {ABC}\) là góc nội tiếp chắn cung CDA của (O) nên \(\widehat {ABC}\)= \(\frac{1}{2}\)sđ\(\overset\frown{CDA}=\frac{ \alpha}{2}.\)
b) Xét (O) có sđ\(\overset\frown{ABC}=360{}^\circ -\)sđ\(\overset\frown{CDA}=360{}^\circ - \alpha.\)
\(\widehat {ADC}\) là góc nội tiếp chắn cung ABC của (O) nên\(\widehat {ADC}\) = \(\frac{1}{2}\)sđ\(\overset\frown{ABC}=\frac{360{}^\circ - \alpha}{2}.\)
c) \(\widehat {ADC} + \widehat {ABC} = \frac{{360^\circ - \alpha}}{2} + \frac{ \alpha}{2} = \frac{{360^\circ - \alpha + \alpha}}{2} = 180^\circ .\)
LT2
Trả lời câu hỏi Luyện tập 2 trang 76 SGK Toán 9 Cánh diều
Cho đường tròn (O) ngoại tiếp tam giác đều ABC và điểm M thuộc cung nhỏ BC (M khác B và C). Tính số đo góc BMC.
Phương pháp giải:
Bước 1: Tính số đo cung AB và AC.
Bước 2: \(\widehat {BMC} = \frac{1}{2}\)sđ\(\overset\frown{BAC}.\)
Lời giải chi tiết:
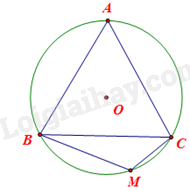
Vì tam giác ABC đều nên \(\widehat {ABC} = \widehat {ACB} = 60^\circ .\) Mà tam giác ABC và nội tiếp (O) nên sđ\(\overset\frown{AB}=2\)\(\widehat {ACB}\), sđ\(\overset\frown{AC}=2\)\(\widehat {ABC}\).
Suy ra sđ\(\overset\frown{AB}=\)sđ\(\overset\frown{AC}=2.60{}^\circ =120{}^\circ .\) Do đó
sđ\(\overset\frown{BAC}=\) sđ\(\overset\frown{AB}+\)sđ\(\overset\frown{AC}=120{}^\circ +120{}^\circ =240{}^\circ .\)
Góc BMC là góc nội tiếp chắn cung BAC của (O) nên \(\widehat {BMC} = \frac{1}{2}\)sđ\(\overset\frown{BAC}=\frac{1}{2}.240{}^\circ =120{}^\circ .\)
Vậy \(\widehat {BMC} = 120^\circ .\)