Giải mục 3 trang 35, 36, 37 SGK Toán 11 tập 1 - Cánh Diều
a) Đường thẳng (d:y = frac{1}{2}) cắt đồ thị hàm số (y = cos x,x in left[ { - pi ;pi } right]) tại hai giao điểm ({C_0},{D_0}) (Hình 35). Tìm hoành độ giao điểm của hai giao điểm ({C_0},{D_0}).
HĐ 4
a) Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \cos x,x \in \left[ { - \pi ;\pi } \right]\) tại hai giao điểm \({C_0},{D_0}\) (Hình 35). Tìm hoành độ giao điểm của hai giao điểm \({C_0},{D_0}\).
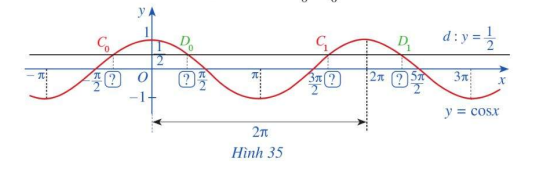
b) Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \cos x,x \in \left[ {\pi ;3\pi } \right]\) tại hai giao điểm \({C_1},{D_1}\) (Hình 35). Tìm hoành độ giao điểm của hai giao điểm \({C_1},{D_1}\).
Phương pháp giải:
Dựa vào kiến thức đã học về lượng giác để xác định tọa độ giao điểm
Lời giải chi tiết:
a) Hoành độ của \({C_0}\) là \( - \frac{\pi }{3}\)
Hoành độ của \({D_0}\) là \(\frac{\pi }{3}\)
b) Hoành độ của \({C_1}\) là \(\frac{{5\pi }}{3}\)
Hoành độ của \({D_1}\) là \(\frac{{7\pi }}{3}\)
LT - VD 5
a) Giải phương trình \(\cos x = - \frac{1}{2}\)
b) Tìm góc lượng giác x sao cho \(\cos x = \cos \left( { - {{87}^ \circ }} \right)\)
Phương pháp giải:
Sử dụng công thức tổng quát của phương trình cos
Lời giải chi tiết:
a) \(\cos x = - \frac{1}{2} \Leftrightarrow \cos x = \cos \left( {\frac{{2\pi }}{3}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \frac{{2\pi }}{3} + k2\pi \\x = - \frac{{2\pi }}{3} + k2\pi \end{array} \right.\)
b) \(\cos x = \cos \left( { - {{87}^ \circ }} \right) \Leftrightarrow \left[ \begin{array}{l}x = - {87^ \circ } + k.360\\x = {87^ \circ } + k{.360^ \circ }\end{array} \right.\)
LT - VD 6
Giải phương trình được nêu trong bài toán mở đầu.
Phương pháp giải:
Sử dụng công thức tổng quát của phương trình cos
Lời giải chi tiết:
+) Vệ tinh cách mặt đất 1 000 km thì h=1 000
Khi đó
\(\begin{array}{l}1000 = 550 + 450.\cos \frac{\pi }{{50}}t\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = 1\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = \cos 0\\ \Leftrightarrow \frac{\pi }{{50}}t = 0 + k2\pi \\ \Leftrightarrow t = 100.k\,\,\,\,;k \in N*\end{array}\)
+) Vệ tinh cách mặt đất 250 km thì h=250
Khi đó
\(\begin{array}{l}250 = 550 + 450.\cos \frac{\pi }{{50}}t\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = - \frac{2}{3}\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{{50}}t = \arccos \left( { - \frac{2}{3}} \right) + k2\pi \\\frac{\pi }{{50}}t = - \arccos \left( { - \frac{2}{3}} \right) + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{{50}}{\pi }\left[ {\arccos \left( { - \frac{2}{3}} \right) + k2\pi } \right]\\t = \frac{{50}}{\pi }\left[ { - \arccos \left( { - \frac{2}{3}} \right) + k2\pi } \right]\end{array} \right.;k \in N*\end{array}\)
+) Vệ tinh cách mặt đất 100 km thì h=100
Khi đó
\(\begin{array}{l}100 = 550 + 450.\cos \frac{\pi }{{50}}t\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = - 1\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = \cos \pi \\ \Leftrightarrow \frac{\pi }{{50}}t = \pi + k2\pi \\ \Leftrightarrow t = 50 + 100k\,\,\,\,;k \in N*\end{array}\)