Giải mục 3 trang 67, 68, 69 SGK Toán 11 tập 2 - Chân trời sáng tạo — Không quảng cáo

Hoạt động 4

Cho đường thẳng $a$ vuông góc với mặt phẳng $\left( Q \right)$. Mặt phẳng $\left( P \right)$ chứa $a$ và cắt $\left( Q \right)$ theo giao tuyến $c$. Trong $\left( Q \right)$ ta vẽ đường thẳng $b$ vuông góc với $c$.

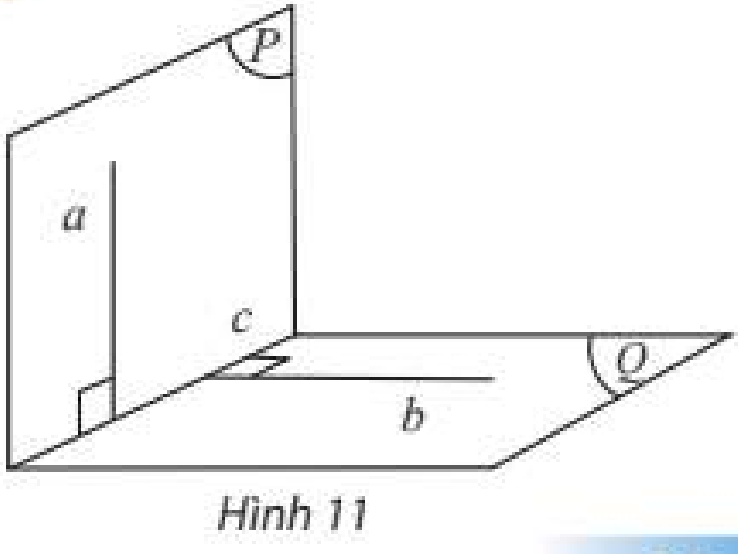
Hỏi:

a) $\left( P \right)$ có vuông góc với $\left( Q \right)$ không?

b) Đường thẳng $b$ vuông góc với $\left( P \right)$ không?

Phương pháp giải:

Sử dụng định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

Lời giải chi tiết:

a) Ta có:

$\left. \begin{array}{l}a \bot \left( Q \right)\\a \subset \left( P \right)\end{array} \right\} \Rightarrow \left( P \right) \bot \left( Q \right)$

b) Ta có:

$\left. \begin{array}{l}\left. \begin{array}{l}a \bot \left( Q \right)\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow a \bot b\\b \bot c\\a,c \subset \left( P \right)\end{array} \right\} \Rightarrow b \bot \left( P \right)$

Hoạt động 5

Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ cùng vuông góc với mặt phẳng $\left( R \right)$. Gọi $a$ là giao tuyến của $\left( P \right)$ và $\left( Q \right)$. Lấy điểm $M$ trong $\left( R \right)$, vẽ hai đường thẳng $MH$ và $MK$ lần lượt vuông góc với $\left( P \right)$ và $\left( Q \right)$. Hỏi:

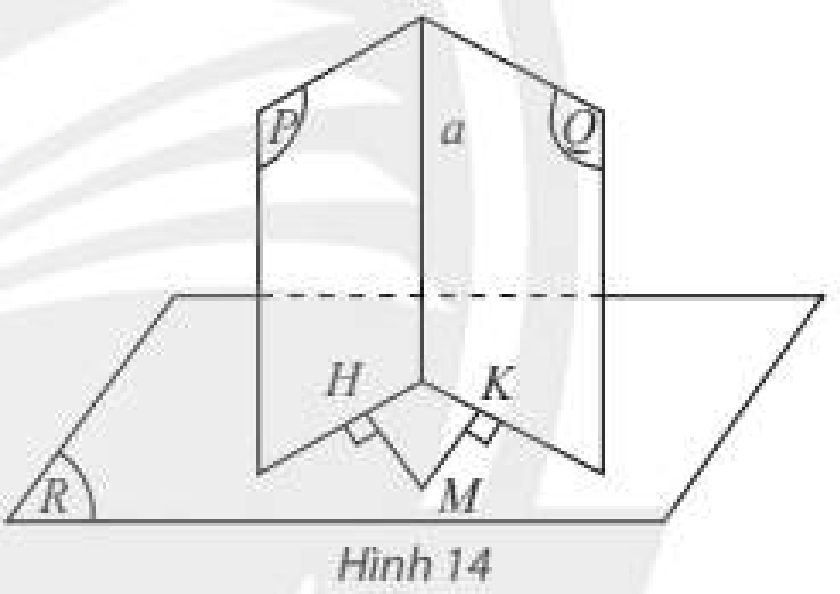
a) Hai đường thẳng $MH$ và $MK$ có nằm trong $\left( R \right)$ không?

b) Đường thẳng $a$ có vuông góc với $\left( R \right)$ không?

Phương pháp giải:

Sử dụng định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

Lời giải chi tiết:

a) Ta có:

$\begin{array}{l}\left. \begin{array}{l}M \in \left( R \right)\\MH \bot \left( P \right)\\\left( R \right) \bot \left( P \right)\end{array} \right\} \Rightarrow MH \subset \left( R \right)\\\left. \begin{array}{l}M \in \left( R \right)\\MK \bot \left( Q \right)\\\left( R \right) \bot \left( Q \right)\end{array} \right\} \Rightarrow MK \subset \left( R \right)\end{array}$

b) Ta có:

$\left. \begin{array}{l}MH \bot \left( P \right) \Rightarrow MH \bot a\\MK \bot \left( Q \right) \Rightarrow MK \bot a\\MH,MK \subset \left( R \right)\end{array} \right\} \Rightarrow a \bot \left( R \right)$

Thực hành 2

Tứ diện $ABCD$ có $AB \bot \left( {BCD} \right)$. Trong tam giác $BCD$ vẽ đường cao $BE$ và $DF$ cắt nhau tại $O$. Trong mặt phẳng $\left( {ACD} \right)$ vẽ ${\rm{D}}K$ vuông góc với $AC$ tại $K$. Gọi $H$ là trực tâm của tam giác $ACD$. Chứng minh rằng:

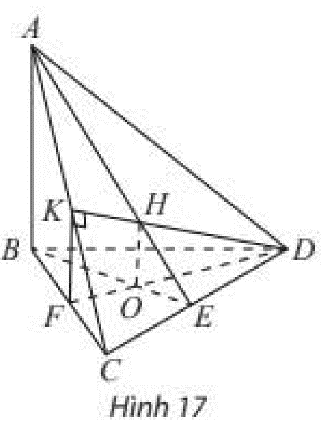
a) $\left( {ADC} \right) \bot \left( {ABE} \right)$ và $\left( {ADC} \right) \bot \left( {DFK} \right)$;

b) $OH \bot \left( {ADC} \right)$.

Phương pháp giải:

‒ Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng.

‒ Cách chứng minh đường thẳng vuông góc với mặt phẳng:

+ Cách 1: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.

+ Cách 2: sử dụng định lí: Nếu hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.

Lời giải chi tiết:

a) Ta có:

$\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot C{\rm{D}}\\BE \bot CE\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABE} \right)$

Lại có $C{\rm{D}} \subset \left( {A{\rm{D}}C} \right)$

Vậy $\left( {ADC} \right) \bot \left( {ABE} \right)$

$\begin{array}{l}\left. \begin{array}{l}AB \bot \left( {BC{\rm{D}}} \right) \Rightarrow AB \bot DF\\DF \bot BC\end{array} \right\} \Rightarrow DF \bot \left( {ABC} \right)\\\left. \begin{array}{l} \Rightarrow DF \bot AC\\DK \bot AC\end{array} \right\} \Rightarrow AC \bot \left( {DFK} \right)\end{array}$

Lại có $AC \subset \left( {A{\rm{D}}C} \right)$

Vậy $\left( {ADC} \right) \bot \left( {DFK} \right)$

b) Ta có:

$\left. \begin{array}{l}\left( {ADC} \right) \bot \left( {ABE} \right)\\\left( {ADC} \right) \bot \left( {DFK} \right)\\\left( {ABE} \right) \cap \left( {DFK} \right) = OH\end{array} \right\} \Rightarrow OH \bot \left( {ADC} \right)$

Vận dụng 2

Nêu cách đặt một quyển sách lên mặt bàn sao cho tất cả các trang sách đều vuông góc với mặt bàn.

Phương pháp giải:

Sử dụng định lí: Nếu hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.

Lời giải chi tiết:

Ta mở quyển sách ra và đặt quyển sách lên mặt bàn sao cho hai mép dưới của bìa sách nằm trên mặt bàn.