Giải mục 4 trang 102, 103 SGK Toán 11 tập 2 - Cánh Diều — Không quảng cáo

Hoạt động 3

Trong Hình 67 , thanh gỗ dọc phía trên các cột và mặt đường hành lang gợi nên hình ảnh đường thẳng $\Delta$ và mặt phẳng $\left( P \right)$ song song với nhau, chiều cao của chiếc cột có đỉnh cột $A$ là khoảng cách từ điểm $A$ đến mặt phẳng $\left( P \right)$.

a) Khoảng cách từ điểm $A$ đến mặt phẳng $\left( P \right)$ có phụ thuộc vào vị trí của điểm $A$ trên đường thẳng $\Delta$ hay không? Vì sao?

b) Khoảng cách đó gợi nên khái niệm nào trong hình học liên quan đến đường thẳng $\Delta$ và mặt phẳng $\left( P \right)$?

Phương pháp giải:

Sử dụng tính chất của đường thẳng và mặt phẳng song song.

Lời giải chi tiết:

a) Trên đường thẳng $\Delta$ lấy điểm $B$ khác $A$.

Kẻ $AH \bot \left( P \right),BK \bot \left( P \right)\left( {H,K \in \left( P \right)} \right)$

$\Rightarrow ABKH$ là hình chữ nhật $\Rightarrow AH = BK$

$\Rightarrow d\left( {A,\left( P \right)} \right) = d\left( {B,\left( P \right)} \right)$

Vậy khoảng cách từ điểm $A$ đến mặt phẳng $\left( P \right)$ không phụ thuộc vào vị trí của điểm $A$ trên đường thẳng $\Delta$.

b) Khoảng cách đó gợi nên khái niệm khoảng cách giữa đường thẳng và mặt phẳng song song.

Luyện tập 3

Cho hình chóp $S.ABC$ có $SA = a$, góc giữa $SA$ và $mp\left( {ABC} \right)$ là ${60^ \circ }$. Gọi $M,N$ lần lượt là trung điểm của cạnh $SA$ và $SB$. Chứng minh $MN\parallel \left( {ABC} \right)$ và tính $d\left( {MN,\left( {ABC} \right)} \right)$.

Phương pháp giải:

‒ Cách chứng minh đường thẳng song song với mặt phẳng: Chứng minh đường thẳng đó song song với một đường thẳng nằm trên mặt phẳng.

‒ Cách tính khoảng cách giữa đường thẳng và mặt phẳng song song: Tính khoảng cách từ một điểm trên đường thẳng đến mặt phẳng.

Lời giải chi tiết:

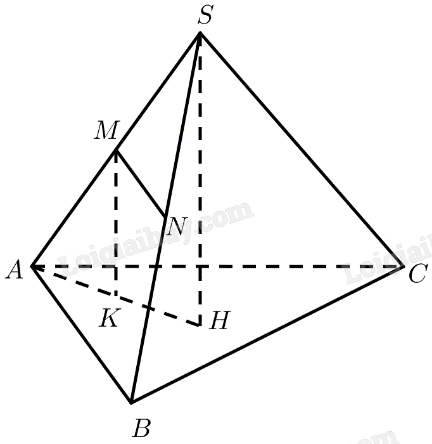
Ta có: $M$ là trung điểm của $SA$

$N$ là trung điểm của $SB$

$\Rightarrow MN$ là đường trung bình của $\Delta SAB$

$\left. \begin{array}{l} \Rightarrow MN\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {ABC} \right)$

$\Rightarrow d\left( {MN,\left( {ABC} \right)} \right) = d\left( {M,\left( {ABC} \right)} \right)$

Gọi $H$ là hình chiếu vuông góc của $S$ lên $\left( {ABC} \right)$$\Rightarrow SH \bot \left( {ABC} \right)$

Qua $M$ kẻ đường thẳng song song với $SH$, cắt $\left( {ABC} \right)$ tại $K$

$\Rightarrow K \in AH,MK \bot \left( {ABC} \right) \Rightarrow d\left( {M,\left( {ABC} \right)} \right) = MK$

$\begin{array}{l}SH \bot \left( {ABC} \right) \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = \left( {SA,HA} \right) = \widehat {SAH} = {60^ \circ }\\ \Rightarrow SH = SA.\sin \widehat {SAH} = \frac{{a\sqrt 3 }}{2}\end{array}$

$M$ là trung điểm của $SA$, $MK\parallel SH$

$\Rightarrow MK$ là đường trung bình của $\Delta SAH$

$\Rightarrow MK = \frac{1}{2}AH = \frac{{a\sqrt 3 }}{4}$

Vậy $d\left( {MN,\left( {ABC} \right)} \right) = \frac{{a\sqrt 3 }}{4}$