Giải mục II trang 75, 76 SGK Toán 10 tập 2 - Cánh diều
Cho đường thẳng có phương trình tổng quát ax + bx + c = 0 (a hoặc b khác 0). Nêu nhận xét về vị trí tương đối của đường thẳng với các trục toạ độ trong môi trường hợp sau:
Hoạt động 3
Trong mặt phẳng toạ độ Oxy, cho đường thẳng \(\Delta \). Vẽ vectơ \(\overrightarrow n \) (\(\overrightarrow n \ne \overrightarrow 0 \)) có giá vuông góc với đường thẳng \(\Delta \).
Lời giải chi tiết:
Nhận xét
• Nếu \(\overrightarrow n \) là một vectơ pháp tuyến của \(\Delta \) thì \(k\overrightarrow n \ne \overrightarrow 0 \left( {k \ne 0} \right)\)cũng là một vectơ pháp tuyến của \(\Delta \).
• Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vectơ pháp tuyến của đường thẳng đó.
• Nếu đường thẳng \(\Delta \) có vectơ chỉ phương là \(\overrightarrow u = \left( {a;b} \right)\) thì vectơ \(\overrightarrow n = \left( { - b;a} \right)\)là một vectơ pháp tuyến của \(\Delta \).
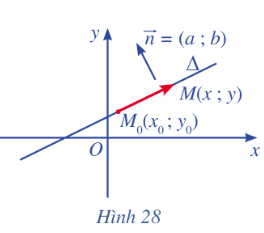
Hoạt động 4
Trong mặt phẳng toạ độ Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_o}\left( {{x_o};{y_o}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n {\rm{ }} = \left( {a;{\rm{ }}b} \right)\). Xét điểm M(x ; y) nằm trên \(\Delta \) (Hình 28).
a) Nhận xét về phương của hai vectơ \(\overrightarrow n \) và \(\overrightarrow {{M_o}M} \).
b) Tìm mối liên hệ giữa toạ độ của điểm M với toạ độ của điểm \({M_o}\) và toạ độ của vectơ pháp tuyến \(\overrightarrow n \).
Lời giải chi tiết:
a) Phương của hai vecto \(\overrightarrow n \) và \(\overrightarrow {{M_o}M} \) vuông góc với nhau.
b) Ta có: \(\overrightarrow {{M_o}M} = \left( {x - {x_o};y - {y_o}} \right),\overrightarrow u = \left( {a;b} \right)\)
Xét điểm \(M\left( {x;y} \right) \in \Delta \). Vì \(\overrightarrow {{M_o}M} \bot \overrightarrow n \) nên: \(\overrightarrow {{M_o}M} .\overrightarrow n = 0 \Leftrightarrow a\left( {x - {x_o}} \right) + b\left( {y - {y_o}} \right) = 0 \Leftrightarrow ax + by - a{x_o} + b{y_o} = 0\)
Luyện tập – vận dụng 2
Cho đường thẳng \(\Delta \) có phương trình tổng quát là: \(x{\rm{ }}-{\rm{ }}y{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}0\) .
a) Chỉ ra toạ độ của một vectơ pháp tuyến và một vectơ chỉ phương của \(\Delta \).
b) Chỉ ra toạ độ của hai điểm thuộc \(\Delta \).
Lời giải chi tiết:
a) Tọa độ vecto pháp tuyến của \(\Delta \) là: \(\overrightarrow n (1; - 1)\)
Tọa độ vecto chỉ phương của \(\Delta \) là: \(\overrightarrow u (1;1)\)
b) Chọn \(x = 0;x = 1\) ta lần được được 2 điểm A và B thuộc đường thẳng \(\Delta \) là: \(A\left( {0;1} \right),B\left( {1;2} \right)\)
Hoạt động 5
Cho đường thẳng \(\Delta \) có phương trình tổng quát ax + bx + c = 0 (a hoặc b khác 0). Nêu nhận xét về vị trí tương đối của đường thẳng \(\Delta \) với các trục toạ độ trong môi trường hợp sau:
a) b = 0 và \(a \ne 0\)
b) \(b \ne 0\) và a = 0
c) \(b \ne 0\) và \(a \ne 0\)
Lời giải chi tiết:
a) Nếu b = 0 và \(a \ne 0\) thì phương trình đường thẳng \(\Delta \) trở thành \(ax + c = 0\) . Khi đó đường thẳng \(\Delta \) song song hoặc trùng với trục \(Oy\) và cắt trục \({\rm{O}}x\) tại điểm \(\left( { - \frac{c}{a};0} \right)\).
b) \(b \ne 0\) và a = 0 thì phương trình đường thẳng \(\Delta \) trở thành \(by + c = 0\) . Khi đó đường thẳng \(\Delta \) song song hoặc trùng với trục \({\rm{O}}x\) và cắt trục \(Oy\) tại điểm \(\left( {0; - \frac{c}{b}} \right)\).
c) Nếu \(b \ne 0\) và \(a \ne 0\)thì phương trình đường thẳng \(\Delta \) có thể viết thành \(y = - \frac{a}{b}x - \frac{c}{b}\). Khi đó, đường thẳng \(\Delta \) là đồ thị hàm số bậc nhất \(y = - \frac{a}{b}x - \frac{c}{b}\)vời hệ số góc là \(k = - \frac{a}{b}\).