Trả lời câu hỏi Bài 8 trang 91 Toán 9 Tập 2 — Không quảng cáo

Đề bài

a) Vẽ đường tròn tâm O bán kính R = 2cm.

b) Vẽ một lục giác đều ABCDEF có tất cả các đỉnh nằm trên đường tròn (O).

c) Vì sao tâm O cách đều các cạnh của lục giác đều ? Gọi khoảng cách này là r.

d) Vẽ đường tròn (O; r).

Lời giải chi tiết

a)

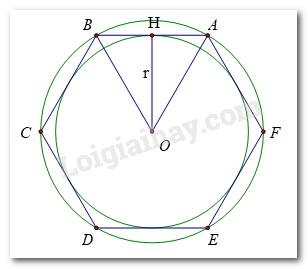
b) Lục giác đều chứa 6 tam giác đều bằng nhau có cạnh = độ dài bán kính

Cách vẽ lục giác đều có tất cả các đỉnh nằm trên đường tròn (O)

Vẽ các dây cung AB = BC = CD = DE = EF = FA = R = 2 cm

c) Vì các dây cung AB = BC = CD = DE = EF = FA bằng nhau nên khoảng cách từ O đến các dây là bằng nhau ( định lí liên hệ giữa dây cung và khoảng cách từ tâm đến dây)

Áp dụng định lí Pytago trong tam giác vuông OAH, ta có:

$OH^2+AH^2 = OA^2$

$\Rightarrow r^2 + 1^2 = 2^2$

$\Rightarrow r^2 =3$

$\Rightarrow r= \sqrt{3}$ cm

d) Vẽ đường tròn tâm O, bán kính $r = \sqrt{3}$ cm