Trắc nghiệm Bài 3: Đoạn thẳng Toán 6 Cánh diều
Đề bài
Kể tên các đoạn thẳng có trong hình vẽ dưới đây

-
A.
$MN;\,MQ;NQ;ML;LP;MP;NP;QL$
-
B.
$MN;QL;MQ;NQ;ML;LP;MP$
-
C.
$MN;\,MQ;NQ;ML;QL;MP;NP$
-
D.
$MN;\,MQ;ML;MP;NP$
Cho G là một điểm thuộc đoạn thẳng HK ( G không trùng với H và K). Hỏi trong ba điểm G, H, K, điểm nào nằm giữa hai điểm còn lại?
-
A.
Điểm G
-
B.
Điểm H
-
C.
Điểm K
-
D.
Không có điểm nào nằm giữa hai điểm còn lại.
Cho $10$ điểm phân biệt trong đó không có ba điểm nào thẳng hàng, cứ qua hai điểm ta vẽ một đoạn thẳng. Hỏi vẽ được tất cả bao nhiêu đoạn thẳng?
-
A.
$10$
-
B.
$90$
-
C.
$40$
-
D.
$45$
Cho $n$ điểm phân biệt $\left( {n \ge 2;\,n \in N} \right)$ trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng nối hai trong $n$ điểm đó. Có tất cả $28$ đoạn thẳng. Hãy tìm $n.$
-
A.
$n = 9.$
-
B.
$n = 7.$
-
C.
$n = 8.$
-
D.
$n = 6.$
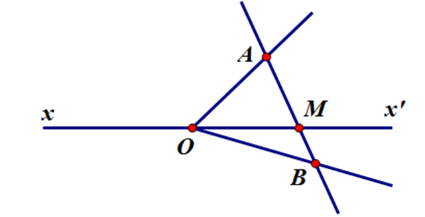
Đường thẳng \(xx'\) cắt bao nhiêu đoạn thẳng trên hình vẽ sau
-
A.
$3$
-
B.
$4$
-
C.
$5$
-
D.
$6$
Cho các đoạn thẳng \(AB = 4cm;\,MN = 5cm;\,EF = 3\,cm;\,PQ = 4cm;\,IK = 5\,cm\). Chọn đáp án sai.
-
A.
\(AB < MN\)
-
B.
$EF < IK$
-
C.
\(AB = PQ\)
-
D.
\(AB = EF\)
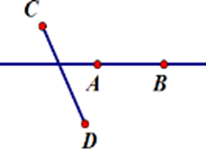
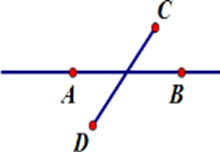
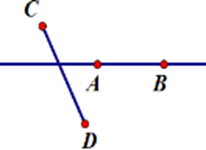
Hãy chọn hình vẽ đúng theo diễn đạt sau: Vẽ đoạn thẳng $AB$ không cắt đoạn thẳng $CD$ nhưng đường thẳng $AB$ cắt đoạn thẳng $CD.$
-
A.

-
B.

-
C.
-
D.
Cho $E$ là điểm nằm giữa hai điểm $I$ và $K.$ Biết rằng $IE = 4cm,EK = 10cm.$Tính độ dài đoạn thẳng $IK.$
-
A.
$4cm$
-
B.
$7cm$
-
C.
$6cm$
-
D.
$14cm$
Cho đoạn thẳng $IK = 8cm$. Điểm $P$ nằm giữa hai điểm $I$ và $K$ sao cho \(IP - PK = 4cm.\) Tính độ dài các đoạn thẳng $PI$ và $PK.$
-
A.
\(IP = 2cm;PK = 6cm.\)
-
B.
\(IP = 3cm;PK = 5cm.\)
-
C.
\(IP = 6cm;PK = 2cm.\)
-
D.
\(IP = 5cm;PK = 1cm.\)
Cho đoạn thẳng $AB = 4,5cm$ và điểm $C$ nằm giữa hai điểm $A$ và $B$. Biết $AC = \dfrac{2}{3}CB$. Tính độ dài đoạn thẳng $AC$ và $BC.$
-
A.
$BC = 2,7cm;\,AC = 1,8cm.$
-
B.
$BC = 1,8cm;\,AC = 2,7cm.$
-
C.
$BC = 1,8cm;\,AC = 1,8cm.$
-
D.
$BC = 2cm;\,AC = 3cm.$
$M$ là trung điểm của đoạn thẳng $AB$ khi và chỉ khi:
-
A.
$MA = MB$
-
B.
\(AM = \dfrac{1}{2}AB\)
-
C.
\(MA + MB = AB\)
-
D.
$MA + MB = AB$ và $MA = MB$
Nếu ta có \(P\) là trung điểm của \(MN\) thì
-
A.
\(MP = NP = \dfrac{{MN}}{2}\)
-
B.
\(MP + NP = 2MN\)
-
C.
\(MP = NP = \dfrac{{MN}}{4}\)
-
D.
\(MP = NP = MN\)
Cho đoạn thẳng $AB$ dài $12cm$, $M$ là trung điểm của đoạn thẳng $AB.$ Khi đó, độ dài của đoạn thẳng $MA$ bằng
-
A.
$3cm$
-
B.
$15cm$
-
C.
$6cm$
-
D.
$20cm$
Cho $I$ là trung điểm của đoạn thẳng $MN.$ Biết $NI = 8cm$. Khi đó, độ dài của đoạn thẳng $MN$ bằng
-
A.
$4cm$
-
B.
$16cm$
-
C.
$21cm$
-
D.
$24cm$
Cho đoạn thẳng $AB.$Gọi $M$ và $N$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AM.$ Giả sử $AN = 1,5cm$. Đoạn thẳng $AB$ có độ dài là?
-
A.
$1,5cm$
-
B.
$3cm$
-
C.
$4,5cm$
-
D.
$6cm$
Cho đoạn thẳng $AB = 8cm$. Gọi $I$ và $K$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AI.$ Đoạn thẳng $IK$ có độ dài là?
-
A.
$8cm$
-
B.
$4cm$
-
C.
$2cm$
-
D.
$6cm$
Lời giải và đáp án
Kể tên các đoạn thẳng có trong hình vẽ dưới đây

-
A.
$MN;\,MQ;NQ;ML;LP;MP;NP;QL$
-
B.
$MN;QL;MQ;NQ;ML;LP;MP$
-
C.
$MN;\,MQ;NQ;ML;QL;MP;NP$
-
D.
$MN;\,MQ;ML;MP;NP$
Đáp án : A
Sử dụng định nghĩa đoạn thẳng: “Đoạn thẳng \(AB\) là hình gồm điểm A, điểm B và tất cả các điểm nằm giữa A và B” để xác định các đoạn thẳng có trên hình vẽ.
Các đoạn thẳng có trên hình vẽ là:
$MN;\,MQ;NQ;ML;LP;MP;NP;QL$
Cho G là một điểm thuộc đoạn thẳng HK ( G không trùng với H và K). Hỏi trong ba điểm G, H, K, điểm nào nằm giữa hai điểm còn lại?
-
A.
Điểm G
-
B.
Điểm H
-
C.
Điểm K
-
D.
Không có điểm nào nằm giữa hai điểm còn lại.
Đáp án : A
Dựa vào dấu hiệu nhận biết một điểm nằm giữa hai điểm.
“Nếu điểm $M$ thuộc đoạn thẳng $AB$ thì điểm $M$ nằm giữa hai điểm $A$ và $B$”
Vì G là một điểm thuộc đoạn thẳng HK nên G nằm giữa hai điểm H và K.
Cho $10$ điểm phân biệt trong đó không có ba điểm nào thẳng hàng, cứ qua hai điểm ta vẽ một đoạn thẳng. Hỏi vẽ được tất cả bao nhiêu đoạn thẳng?
-
A.
$10$
-
B.
$90$
-
C.
$40$
-
D.
$45$
Đáp án : D
Sử dụng cách tính số đoạn thẳng:
Với \(n\) điểm cho trước \(\left( {n \in N;\,n \ge 2} \right)\) và không có ba điểm nào thẳng hàng thì số đoạn thẳng vẽ được là \(\dfrac{{n.\left( {n - 1} \right)}}{2}\) .
Số đoạn thẳng cần tìm là
$\dfrac{{10.\left( {10 - 1} \right)}}{2} = 45$ đoạn thẳng
Cho $n$ điểm phân biệt $\left( {n \ge 2;\,n \in N} \right)$ trong đó không có ba điểm nào thẳng hàng. Vẽ các đoạn thẳng nối hai trong $n$ điểm đó. Có tất cả $28$ đoạn thẳng. Hãy tìm $n.$
-
A.
$n = 9.$
-
B.
$n = 7.$
-
C.
$n = 8.$
-
D.
$n = 6.$
Đáp án : C
Sử dụng công thức tính số đoạn thẳng:
Với \(n\) điểm cho trước \(\left( {n \in N;\,n \ge 2} \right)\) và không có ba điểm nào thẳng hàng thì số đoạn thẳng vẽ được là \(\dfrac{{n.\left( {n - 1} \right)}}{2}\) .
Từ đó tìm ra $n.$
Số đoạn thẳng tạo thành từ $n$ điểm phân biệt trong đó không có ba điểm nào thẳng hàng là $\dfrac{{n\left( {n - 1} \right)}}{2}$ $\left( {n \ge 2;\,n \in N} \right)$
Theo đề bài có $28$ đoạn thẳng được tạo thành nên ta có $\dfrac{{n\left( {n - 1} \right)}}{2} = 28 \Rightarrow n\left( {n - 1} \right) = 56 = 8.7$
Nhận thấy $\left( {n - 1} \right)$ và $n$ là hai số tự nhiên liên tiếp, suy ra $n = 8.$
Đường thẳng \(xx'\) cắt bao nhiêu đoạn thẳng trên hình vẽ sau

-
A.
$3$
-
B.
$4$
-
C.
$5$
-
D.
$6$
Đáp án : C
Sử dụng kiến thức về đường thẳng và đoạn thẳng cắt nhau:
“Nếu một đoạn thẳng chỉ có một điểm chung với đường thẳng thì chúng cắt nhau.”
Đường thẳng $xx'$ cắt năm đoạn thẳng $OA;OB;AB$; $MA;MB$
Cho các đoạn thẳng \(AB = 4cm;\,MN = 5cm;\,EF = 3\,cm;\,PQ = 4cm;\,IK = 5\,cm\). Chọn đáp án sai.
-
A.
\(AB < MN\)
-
B.
$EF < IK$
-
C.
\(AB = PQ\)
-
D.
\(AB = EF\)
Đáp án : D
Sử dụng kiến thức về so sánh hai đoạn thẳng
- Hai đoạn thẳng bằng nhau nếu có cùng độ dài.
- Đoạn thẳng lớn hơn nếu có độ dài lớn hơn.
+ Đáp án A: \(AB < MN\) là đúng vì $AB = 4cm < 5cm = MN$.
+ Đáp án B: $EF < IK$ là đúng vì $EF = 3cm < 5cm = IK$
+ Đáp án C: \(AB = PQ\) là đúng vì hai đoạn cùng có độ dài $4cm$
+ Đáp án D: \(AB = EF\) là sai vì $AB = 4cm > 3cm = EF$.
Hãy chọn hình vẽ đúng theo diễn đạt sau: Vẽ đoạn thẳng $AB$ không cắt đoạn thẳng $CD$ nhưng đường thẳng $AB$ cắt đoạn thẳng $CD.$
-
A.

-
B.

-
C.

-
D.

Đáp án : C
Sử dụng kiến thức:
Nếu một đoạn thẳng chỉ có một điểm chung với đường thẳng, tia hoặc đoạn thẳng khác thì chúng cắt nhau.
Đoạn thẳng $AB$ không cắt đoạn thẳng $CD$ nhưng đường thẳng $AB$ cắt đoạn thẳng $CD$ nghĩa là đoạn thẳng $AB$ không có điểm chung với đoạn thẳng $CD$ và đường thẳng $AB$có duy nhất một điểm chung với đoạn thẳng $CD.$
Hình vẽ thể hiện đúng diễn đạt trên là
Cho $E$ là điểm nằm giữa hai điểm $I$ và $K.$ Biết rằng $IE = 4cm,EK = 10cm.$Tính độ dài đoạn thẳng $IK.$
-
A.
$4cm$
-
B.
$7cm$
-
C.
$6cm$
-
D.
$14cm$
Đáp án : D
$E$ là điểm nằm giữa hai điểm $I$ và $K$ nên ta có công thức cộng đoạn thẳng $IE + EK = IK$. Biết độ dài $IL, LK$, thay số vào ta tính được độ dài đoạn thẳng $IK.$
Vì $E$ là điểm nằm giữa hai điểm $I$ và $K$ nên ta có $IE + EK = IK$
Hay $4 + 10 = IK$ suy ra $IK = 14\,cm.$
Cho đoạn thẳng $IK = 8cm$. Điểm $P$ nằm giữa hai điểm $I$ và $K$ sao cho \(IP - PK = 4cm.\) Tính độ dài các đoạn thẳng $PI$ và $PK.$
-
A.
\(IP = 2cm;PK = 6cm.\)
-
B.
\(IP = 3cm;PK = 5cm.\)
-
C.
\(IP = 6cm;PK = 2cm.\)
-
D.
\(IP = 5cm;PK = 1cm.\)
Đáp án : C
Sử dụng công thức cộng đoạn thẳng $PI + IK = PK$ và dữ kiện đề bài để tìm độ dài hai đoạn thẳng $PI;PK.$

Vì điểm $P$ nằm giữa hai điểm $I$ và $K$ nên ta có $PI + PK = IK \Rightarrow PI + IK = 8cm$ (1)
Theo đề bài \(IP - PK = 4cm\)(2)
Từ (1) và (2) suy ra \(IP = \dfrac{{8 + 4}}{2} = 6cm\) và \(PK = \dfrac{{8 - 4}}{2} = 2cm\)
Vậy \(IP = 6cm;PK = 2cm.\)
Cho đoạn thẳng $AB = 4,5cm$ và điểm $C$ nằm giữa hai điểm $A$ và $B$. Biết $AC = \dfrac{2}{3}CB$. Tính độ dài đoạn thẳng $AC$ và $BC.$
-
A.
$BC = 2,7cm;\,AC = 1,8cm.$
-
B.
$BC = 1,8cm;\,AC = 2,7cm.$
-
C.
$BC = 1,8cm;\,AC = 1,8cm.$
-
D.
$BC = 2cm;\,AC = 3cm.$
Đáp án : A
Sử dụng công thức cộng đoạn thẳng $AC + CB = AB$ và dữ kiện đề bài $AC = \dfrac{2}{3}CB$ để tính độ dài mỗi đoạn thẳng $AC$ và $BC.$
Vì điểm $C$ nằm giữa hai điểm $A$ và $B$ nên ta có $AC + CB = AB$ (1)
Thay $AC = \dfrac{2}{3}CB$ (theo đề bài) vào (1) ta được $\dfrac{2}{3}CB + CB = AB$ $ \Rightarrow CB.\left( {\dfrac{2}{3} + 1} \right) = 4,5$
$ \Rightarrow CB.\dfrac{5}{3} = \dfrac{9}{2}$$ \Rightarrow BC = \dfrac{9}{2}:\dfrac{5}{3} = \dfrac{{27}}{{10}} = 2,7\,cm$
Từ đó $AC = \dfrac{2}{3}BC = \dfrac{2}{3}.2,7 = 1,8cm$.
Vậy $BC = 2,7cm;\,AC = 1,8cm.$
$M$ là trung điểm của đoạn thẳng $AB$ khi và chỉ khi:
-
A.
$MA = MB$
-
B.
\(AM = \dfrac{1}{2}AB\)
-
C.
\(MA + MB = AB\)
-
D.
$MA + MB = AB$ và $MA = MB$
Đáp án : D
\(M\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow \left\{ \begin{array}{l}AM + MB = AB\\{\rm{MA = MB}}\end{array} \right.$
Nếu ta có \(P\) là trung điểm của \(MN\) thì
-
A.
\(MP = NP = \dfrac{{MN}}{2}\)
-
B.
\(MP + NP = 2MN\)
-
C.
\(MP = NP = \dfrac{{MN}}{4}\)
-
D.
\(MP = NP = MN\)
Đáp án : A
Ta có \(P\) là trung điểm của \(MN\) thì \(MP = NP = \dfrac{{MN}}{2}\)
Cho đoạn thẳng $AB$ dài $12cm$, $M$ là trung điểm của đoạn thẳng $AB.$ Khi đó, độ dài của đoạn thẳng $MA$ bằng
-
A.
$3cm$
-
B.
$15cm$
-
C.
$6cm$
-
D.
$20cm$
Đáp án : C
Sử dụng kiến thức \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$
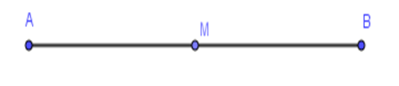
Vì \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = }}\dfrac{1}{2}AB = \dfrac{1}{2}.12 = 6cm$
Vậy $AM = 6cm$.
Cho $I$ là trung điểm của đoạn thẳng $MN.$ Biết $NI = 8cm$. Khi đó, độ dài của đoạn thẳng $MN$ bằng
-
A.
$4cm$
-
B.
$16cm$
-
C.
$21cm$
-
D.
$24cm$
Đáp án : B
Sử dụng kiến thức \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$
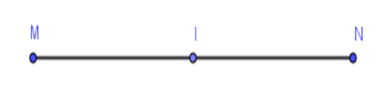
Vì $I$ là trung điểm của đoạn thẳng $MN$ nên $IM = IN = \dfrac{1}{2}MN$ hay $MN = 2.IN = 2.8 = 16cm$.
Cho đoạn thẳng $AB.$Gọi $M$ và $N$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AM.$ Giả sử $AN = 1,5cm$. Đoạn thẳng $AB$ có độ dài là?
-
A.
$1,5cm$
-
B.
$3cm$
-
C.
$4,5cm$
-
D.
$6cm$
Đáp án : D
Sử dụng kiến thức về trung điểm đoạn thẳng : “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính toán.

Vì $N$ là trung điểm đoạn $AM$ nên $AN = \dfrac{1}{2}AM$ hay $AM = 2AN = 2.1,5 = 3cm$
Lại có điểm $M$ là trung điểm đoạn thẳng $AB$ nên ta có $AM = \dfrac{1}{2}AB$ hay $AB = 2AM = 2.3 = 6cm$
Vậy $AB = 6cm$.
Cho đoạn thẳng $AB = 8cm$. Gọi $I$ và $K$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AI.$ Đoạn thẳng $IK$ có độ dài là?
-
A.
$8cm$
-
B.
$4cm$
-
C.
$2cm$
-
D.
$6cm$
Đáp án : C
Sử dụng kiến thức về trung điểm đoạn thẳng : “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính toán.

Vì điểm $I$ là trung điểm đoạn thẳng $AB$ nên $AI = \dfrac{1}{2}AB = \dfrac{1}{2}.8 = 4cm$
Vì điểm $K$ là trung điểm đoạn thẳng $AI$ nên $AK = \dfrac{1}{2}AI = \dfrac{1}{2}.4 = 2cm$
Vậy $AI = 2cm$.