Trắc nghiệm toán 6 bài 4 chương 1 cánh diều có đáp án — Không quảng cáo

Đếm số các số 6 trong tổng.

Sử dụng kết quả: $a.b = a + a + ... + a$ (Có b số hạng)

Kí hiệu của phép nhân là $a \times b$ hoặc $a.b$

Tổng trên có 4 số 6 nên 6+6+6+6=6.4

Đặt tính rồi tính.

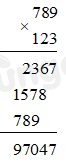
Vậy $789 \times 123 = 97047$

Nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không viết dấu nhân giữa các thừa số.

$4 \times a \times b \times c$ là tích của 4 thừa số:

Thừa số thứ nhất là một số: 4

Thừa số thứ 2, thứ 3, thứ 4 lần lượt là các chữ a,b,c.

Vậy tích này chỉ có 1 thừa số bằng số nên ta có thể bỏ dấu “ $\times$ ” giữa các thừa số đi, tức là

$4 \times a \times b \times c = 4abc$

Tích $\left( {ab} \right)c$ hay $a\left( {bc} \right)$ gọi là tích cả ba số a, b, c và viết gọn là $abc$ .

Tính chất giao hoán: $a.b = b.a$

$\begin{array}{l}\left( {ab} \right)c = \left( {a.b} \right).c = a.b.c = abc\\a\left( {bc} \right) = a.\left( {b.c} \right) = a.b.c = abc\\b\left( {ac} \right) = b.\left( {a.c} \right) = b.a.c = a.b.c = abc\end{array}$

Ta sử dụng (số bị chia) : (số chia) = (thương) để xác định thương của phép chia

Phép chia $x:3 = 6$ có $x$ là số bị chia; $3$ là số chia và $6$ là thương.

Nên thương của phép chia là $6.$

Định nghĩa về phép chia hết và phép chia có dư.

Khi chia a cho b, trong đó $b \ne 0,$ ta luôn tìm được đúng hai số tự nhiên $q$ và $r$ duy nhất sao cho:

$a = b.q + r$ trong đó $0 \le r < b$

Phép chia a cho b là phép chia có dư nên $r \ne 0$

Vậy $0 < r < b$ .

Đặt tính rồi tính.

Xác định a,b,q,r trong phép chia vừa nhận được.

Số bị chia là $b = 445$, số chia là $b = 13$ thương $q = 34$, số dư là $r = 3$. Ta biểu diễn phép chia như sau: $445 = 13.34 + 3$

Đặt tính rồi tính.

Đếm số các phép chia có dư.

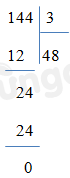
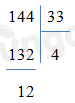
Vậy có 3 phép chia có dư

+ Tính số các số tự nhiên liên tiếp từ $1$ đến $2018$ bằng công thức  (số cuối-số đầu)+1

+ Tổng các số tự nhiên liên tiếp từ $1$ đến $2018$ được tính bằng công thức

(số cuối+số đầu). số các số hạng :2

Số các số tự nhiên liên tiếp từ $1$ đến $2018$ là $2018 - 1 + 1 = 2018$ số

Như vậy từ $1$ đến $2018$ có số các số hạng là $2018.$

Tổng $1 + 2 + 3 + 4 + ... + 2018$$= \left( {2018 + 1} \right).2018:2 = 2037171.$

- Tính trong ngoặc bằng cách sử dụng $ab - ac = a.\left( {b - c} \right).$

- Thực hiện phép chia để tìm kết quả.

Ta có $\left( {158.129 - 158.39} \right):180$$= 158.\left( {129 - 39} \right):180 = 158.90:180$$= 79.2.90:180 = 79.180:180 = 79.$

Vậy kết quả của phép tính có chữ số tận cùng là $9.$

+ Thực hiện phép chia trước

+ Tìm số bị trừ bằng cách lấy hiệu cộng với số trừ

+ Tìm số hạng chưa biết bằng cách lấy tích chia cho số hạng đã biết

Ta có $5x - 46:23 = 18$

$5x - 2 = 18$

$5x = 18 + 2$

$5x = 20$

$x = 20:5$

$x = 4$

Vậy $x = 4.$

Do đó $x$ là số chẵn.