Trắc nghiệm toán 6 các dạng toán bài 3 chương 5 cánh diều có đáp án — Không quảng cáo

Bước 1: Rút gọn các phân số đến tối giản (nếu có thể) Bước 2: Quy đồng mẫu số các phân số sau khi rút gọn Bước 3: Thực hiện cộng hai phân số cùng mẫu ta cộng tử số với tử số, giữ nguyên mẫu số

\(\dfrac{{65}}{{91}} + \dfrac{{ - 44}}{{55}} = \dfrac{5}{7} + \dfrac{{ - 4}}{5}\)\( = \dfrac{{25}}{{35}} + \dfrac{{ - 28}}{{35}} = \dfrac{{ - 3}}{{35}}\)

Thực hiện các phép tính ở mỗi đáp án và kết luận.

Đáp án A: $\dfrac{3}{2} + \dfrac{2}{3} = \dfrac{9}{6} + \dfrac{4}{6} = \dfrac{{13}}{6} > 1$ nên A đúng

Đáp án B: $\dfrac{3}{2} + \dfrac{2}{3} = \dfrac{9}{6} + \dfrac{4}{6} = \dfrac{{13}}{6}$ nên B đúng.

Đáp án C: $\dfrac{3}{4} + \left( {\dfrac{{ - 4}}{{17}}} \right) = \dfrac{{51}}{{68}} + \dfrac{{ - 16}}{{68}} = \dfrac{{35}}{{68}}$ nên C đúng.

Đáp án D: $\dfrac{4}{{12}} + \dfrac{{21}}{{36}} = \dfrac{4}{{12}} + \dfrac{7}{{12}} = \dfrac{{11}}{{12}} < 1$ nên D sai.

Bước 1: Quy đồng mẫu số hai phân số Bước 2: Thực hiện cộng hai phân số cùng mẫu

\(\dfrac{3}{{13}} + \dfrac{9}{{20}} = \dfrac{{60}}{{260}} + \dfrac{{117}}{{260}} = \dfrac{{177}}{{260}}\)

Vậy \(x = \dfrac{{177}}{{260}}\)

Áp dụng tính chất giao hoán và kết hợp của phép cộng phân số, gộp các cặp phân số có tổng bằng $0$  hoặc bằng $1$  lại thành từng nhóm.

\(M = \left( {\dfrac{{21}}{{31}} + \dfrac{{ - 16}}{7}} \right) + \left( {\dfrac{{44}}{{53}} + \dfrac{{10}}{{31}}} \right) + \dfrac{9}{{53}}\)

\(M = \dfrac{{21}}{{31}} + \dfrac{{ - 16}}{7} + \dfrac{{44}}{{53}} + \dfrac{{10}}{{31}} + \dfrac{9}{{53}}\)

\(M = \left( {\dfrac{{21}}{{31}} + \dfrac{{10}}{{31}}} \right) + \left( {\dfrac{{44}}{{53}} + \dfrac{9}{{53}}} \right) + \dfrac{{ - 16}}{7}\)

\(M = 1 + 1 + \dfrac{{ - 16}}{7}\)

\(M = 2 + \dfrac{{ - 16}}{7}\)

\(M = \dfrac{{ - 2}}{7}\)

\(N = \dfrac{1}{2} + \dfrac{{ - 1}}{5} + \dfrac{{ - 5}}{7} + \dfrac{1}{6} + \dfrac{{ - 3}}{{35}} + \dfrac{1}{3} + \dfrac{1}{{41}}\)

\(N = \left( {\dfrac{1}{2} + \dfrac{1}{6} + \dfrac{1}{3}} \right) + \left( {\dfrac{{ - 1}}{5} + \dfrac{{ - 5}}{7} + \dfrac{{ - 3}}{{35}}} \right) + \dfrac{1}{{41}}\)

\(N = \dfrac{{3 + 1 + 2}}{6} + \dfrac{{\left( { - 7} \right) + \left( { - 25} \right) + \left( { - 3} \right)}}{{35}} + \dfrac{1}{{41}}\)

\(N = 1 + \left( { - 1} \right) + \dfrac{1}{{41}}\)

\(N = \dfrac{1}{{41}}\)

Tính các tổng đã cho ở mỗi vế rồi suy ra \(x\) dựa vào quy tắc so sánh hai phân số cùng mẫu số dương, phân số nào lớn hơn thì có tử số lớn hơn.

\(\dfrac{5}{6} + \dfrac{{ - 7}}{8} \le \dfrac{x}{{24}} \le \dfrac{{ - 5}}{{12}} + \dfrac{5}{8}\)

\(\dfrac{{ - 1}}{{24}} \le \dfrac{x}{{24}} \le \dfrac{5}{{24}}\)

\( - 1 \le x \le 5\)

\(x \in \left\{ { - 1;0;1;2;3;4;5} \right\}\)

- Rút gọn biểu thức bài cho rồi chia tách về dạng \(a \pm \dfrac{b}{{n + 1}}\) với \(a,b \in Z\)

- Để giá trị biểu thức là một số nguyên thì \(n + 1 \in Ư\left( b \right)\)

Ta có:

\(\dfrac{{n - 8}}{{n + 1}} + \dfrac{{n + 3}}{{n + 1}}\) \( = \dfrac{{n - 8 + n + 3}}{{n + 1}}\) \( = \dfrac{{2n - 5}}{{n + 1}}\) \( = \dfrac{{\left( {2n + 2} \right) - 7}}{{n + 1}}\) \( = \dfrac{{2\left( {n + 1} \right) - 7}}{{n + 1}}\) \( = \dfrac{{2\left( {n + 1} \right)}}{{n + 1}} - \dfrac{7}{{n + 1}}\) \( = 2 - \dfrac{7}{{n + 1}}\)

Yêu cầu bài toán thỏa mãn nếu \(\dfrac{7}{{n + 1}} \in Z\) hay \(n + 1 \in Ư\left( 7 \right) = \left\{ { \pm 1; \pm 7} \right\}\)

Ta có bảng:

Vậy \(n \in \left\{ {0; - 2;6; - 8} \right\}\)

- Tính lượng nước mỗi vòi chảy được trong mỗi giờ.

- Tính lượng nước cả ba vòi chảy được trong \(1\) giờ.

- Tính số giờ chảy đầy bể của cả ba vòi.

Chú ý: Đối với các dạng toán bể nước hoặc công việc thì ta thường coi đầy bể là \(1\) hoặc công việc hoàn thành là \(1\)

Một giờ vòi \(A\) chảy được là: \(1:6 = \dfrac{1}{6}\) (bể)

Một giờ vòi \(B\) chảy được là: \(1:3 = \dfrac{1}{3}\) (bể)

Một giờ vòi \(C\) chảy được là: \(1:2 = \dfrac{1}{2}\) (bể)

Một giờ cả ba vòi chảy được là: \(\dfrac{1}{6} + \dfrac{1}{3} + \dfrac{1}{2} = \dfrac{6}{6} = 1\) (bể)

Vậy trong \(1\) giờ cả ba vòi chảy được đầy bể.

- Tính tổng \(A\) bằng cách áp dụng công thức \(\dfrac{1}{{n.(n + 1)}} = \dfrac{1}{n} - \dfrac{1}{{n + 1}}\)

- So sánh \(A\) với \(\dfrac{3}{5}\) và \(\dfrac{4}{5}\) rồi kết luận.

\(A = \dfrac{1}{2} + \dfrac{1}{6} + \dfrac{1}{{12}} +  \ldots  + \dfrac{1}{{99.100}}\)

\(A = \dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{99.100}}\)

\(A = 1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{99}} - \dfrac{1}{{100}}\)

\(A = 1 - \dfrac{1}{{100}} = \dfrac{{99}}{{100}}\)

So sánh \(A\) với \(\dfrac{3}{5}\) và \(\dfrac{4}{5}\)

Ta có: \(\dfrac{3}{5} = \dfrac{{60}}{{100}};\dfrac{4}{5} = \dfrac{{80}}{{100}}\)

\( \Rightarrow \dfrac{{60}}{{100}} < \dfrac{{80}}{{100}} < \dfrac{{99}}{{100}}\) \( \Rightarrow A > \dfrac{4}{5} > \dfrac{3}{5}\)

Ta chia thành 3 nhóm, mỗi nhóm 5 số hạng. Sau đó đánh giá để kết luận.

\(S = \dfrac{1}{{21}} + \dfrac{1}{{22}} + \dfrac{1}{{23}} + ... + \dfrac{1}{{35}}\)

\(S = \left( {\dfrac{1}{{21}} + ... + \dfrac{1}{{25}}} \right) + \left( {\dfrac{1}{{26}} + ... + \dfrac{1}{{30}}} \right) + \left( {\dfrac{1}{{31}} + ... + \dfrac{1}{{35}}} \right)\)

\(S > \left( {\dfrac{1}{{25}} + ... + \dfrac{1}{{25}}} \right) + \left( {\dfrac{1}{{30}} + ... + \dfrac{1}{{30}}} \right) + \left( {\dfrac{1}{{35}} + ... + \dfrac{1}{{35}}} \right)\)

\(S > \dfrac{1}{5} + \dfrac{1}{6} + \dfrac{1}{7} = \dfrac{{107}}{{210}} > \dfrac{1}{2}\)

Vậy \(S > \dfrac{1}{2}\).

Ta quy đồng phân số để tìm a, b.

\(\begin{array}{l}\dfrac{a}{5} + \dfrac{1}{{10}} = \dfrac{{ - 1}}{b}\\\dfrac{{2{\rm{a}}}}{{10}} + \dfrac{1}{{10}} = \dfrac{{ - 1}}{b}\\\dfrac{{2{\rm{a}} + 1}}{{10}} = \dfrac{{ - 1}}{b}\\\left( {2{\rm{a}} + 1} \right).b =  - 10\end{array}\)

\(2{\rm{a}} + 1\) là số lẻ; \(2{\rm{a}} + 1\) là ước của \( - 10\)

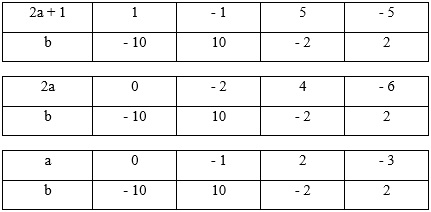
Vậy có \(4\) cặp số \((a;b)\) thỏa mãn bài toán.

Số đối của \(\dfrac{a}{b}\) là \(\dfrac{{ - a}}{b}\) (hoặc \(\dfrac{a}{{ - b}};\; - \dfrac{a}{b}\))

Đáp án A: Số đối của \(\dfrac{{ - 2}}{3}\) là \(\dfrac{2}{3}\) chứ không phải \(\dfrac{3}{2}\) nên A sai.

Đáp án B: Số đối của \(\dfrac{{ - 12}}{{13}}\) là \(\dfrac{{12}}{{13}}\) chứ không phải \(\dfrac{{13}}{{ - 12}}\) nên B sai.

Đáp án C: Số đối của \(\dfrac{1}{2}\) là \( - \dfrac{1}{2}\) nên C đúng.

Đáp án D: Số đối của \(\dfrac{3}{4}\) là \(\dfrac{{ - 3}}{4}\) hoặc \(\dfrac{3}{{ - 4}}\) hoặc \( - \dfrac{3}{4}\) chứ không phải \(\dfrac{{ - 4}}{3}\) nên D sai.

+ Tìm \(x\) bằng cách lấy tổng trừ đi số hạng đã biết

+ Sau đó sử dụng qui tắc trừ hai phân số để tính toán.

\(\begin{array}{l}x + \dfrac{1}{{14}} = \dfrac{5}{7}\\x = \dfrac{5}{7} - \dfrac{1}{{14}}\\x = \dfrac{9}{{14}}\end{array}\)

Thực hiện các phép tính ở mỗi đáp án rồi kết luận.

Đáp án A: \(\dfrac{4}{{13}} - \dfrac{1}{2} = \dfrac{8}{{26}} - \dfrac{{13}}{{26}} = \dfrac{{ - 5}}{{26}} \ne \dfrac{5}{{26}}\) nên A sai.

Đáp án B: \(\dfrac{1}{2} - \dfrac{1}{3} = \dfrac{3}{6} - \dfrac{2}{6} = \dfrac{1}{6} \ne \dfrac{5}{6}\) nên B sai.

Đáp án C: \(\dfrac{{17}}{{20}} - \dfrac{1}{5} = \dfrac{{17}}{{20}} - \dfrac{4}{{20}} = \dfrac{{13}}{{20}}\) nên C đúng.

Đáp án D: \(\dfrac{5}{{15}} - \dfrac{1}{3} = \dfrac{1}{3} - \dfrac{1}{3} = 0 \ne \dfrac{1}{5}\) nên D sai.

Trong biểu thức chỉ chứa phép cộng và phép trừ nên ta tính lần lượt từ trái qua phải.

+) Quy đồng mẫu các phân số sau đó cộng tử với tử, mẫu giữ nguyên.

\(\begin{array}{l}\dfrac{4}{{15}} - \dfrac{2}{{65}} - \dfrac{4}{{39}}\\ = \dfrac{{52}}{{195}} - \dfrac{6}{{195}} - \dfrac{{20}}{{195}}\\ = \dfrac{{52 - 6 - 20}}{{195}}\\ = \dfrac{{26}}{{195}} = \dfrac{2}{{15}}\end{array}\)

Phá dấu ngoặc rồi nhóm các số hạng thích hợp để được tổng hoặc hiệu là các số nguyên rồi tính giá tri biểu thức.

Chú ý quy tắc phá ngoặc đằng trước có dấu \('' - ''\) thì phải đổi dấu.

\(\begin{array}{l}B = \dfrac{{31}}{{23}} - \left( {\dfrac{7}{{30}} + \dfrac{8}{{23}}} \right)\\B = \dfrac{{31}}{{23}} - \dfrac{7}{{30}} - \dfrac{8}{{23}}\\B = \left( {\dfrac{{31}}{{23}} - \dfrac{8}{{23}}} \right) - \dfrac{7}{{30}}\\B = 1 - \dfrac{7}{{30}}\\B = \dfrac{{23}}{{30}}\end{array}\)

Phá ngoặc rồi nhóm các số hạng có tổng hoặc hiệu là một số nguyên rồi thực hiện tính giá trị các biểu thức \(M,N\) và kết luận.

\(\begin{array}{l}M = \left( {\dfrac{1}{3} + \dfrac{{12}}{{67}} + \dfrac{{13}}{{41}}} \right) - \left( {\dfrac{{79}}{{67}} - \dfrac{{28}}{{41}}} \right)\\M = \dfrac{1}{3} + \dfrac{{12}}{{67}} + \dfrac{{13}}{{41}} - \dfrac{{79}}{{67}} + \dfrac{{28}}{{41}}\\M = \dfrac{1}{3} + \left( {\dfrac{{12}}{{67}} - \dfrac{{79}}{{67}}} \right) + \left( {\dfrac{{13}}{{41}} + \dfrac{{28}}{{41}}} \right)\\M = \dfrac{1}{3} + \left( { - 1} \right) + 1\\M = \dfrac{1}{3}\end{array}\)

\(\begin{array}{l}N = \dfrac{{38}}{{45}} - \left( {\dfrac{8}{{45}} - \dfrac{{17}}{{51}} - \dfrac{3}{{11}}} \right)\\N = \dfrac{{38}}{{45}} - \dfrac{8}{{45}} + \dfrac{{17}}{{51}} + \dfrac{3}{{11}}\\N = \left( {\dfrac{{38}}{{45}} - \dfrac{8}{{45}}} \right) + \dfrac{{17}}{{51}} + \dfrac{3}{{11}}\\N = \dfrac{2}{3} + \dfrac{1}{3} + \dfrac{3}{{11}}\\N = 1 + \dfrac{3}{{11}}\\N = \dfrac{{14}}{{11}}\end{array}\)

Vì \(\dfrac{1}{3} < 1 < \dfrac{{14}}{{11}}\) nên \(M < 1 < N\)

Sử dụng quy tắc chuyển vế đổi dấu để tìm \(x\)

\(\begin{array}{l}x - \dfrac{{ - 7}}{{12}} = \dfrac{{17}}{{18}} - \dfrac{1}{9}\\x - \dfrac{{ - 7}}{{12}} = \dfrac{5}{6}\\x = \dfrac{5}{6} + \dfrac{{ - 7}}{{12}}\\x = \dfrac{1}{4}\end{array}\)

Thực hiện phép tính hai vế (rút gọn nếu thể) và tìm \(x\)

\(\dfrac{{ - 5}}{{14}} - \dfrac{{37}}{{14}} \le x \le \dfrac{{31}}{{73}} - \dfrac{{313131}}{{737373}}\)

\(\dfrac{{ - 5}}{{14}} + \dfrac{{ - 37}}{{14}} \le x \le \dfrac{{31}}{{73}} - \dfrac{{313131:10101}}{{737373:10101}}\)

\(\dfrac{{ - 42}}{{14}} \le x \le \dfrac{{31}}{{73}} - \dfrac{{31}}{{73}}\)

\( - 3 \le x \le 0\)

\(x \in \left\{ { - 3; - 2; - 1;0} \right\}\)

Vậy có \(4\) giá trị của \(x\) thỏa mãn bài toán.

- Tìm số phần bể mỗi vòi \(1,2\) chảy được trong \(1\) giờ và số phần bể vòi \(3\) tháo ra.

- Tính số phần bể chảy được trong \(1\) giờ khi mở cả \(3\) vòi.

Trong \(1\) giờ, vòi thứ nhất chảy được là: \(1:10 = \dfrac{1}{{10}}\) (bể)

Trong \(1\) giờ, vòi thứ hai chảy được là: \(1:8 = \dfrac{1}{8}\) (bể)

Trong \(1\) giờ, vòi thứ ba tháo được là: \(1:5 = \dfrac{1}{5}\) (bể)

Sau \(1\) giờ, lượng nước trong bể có là:

\(\dfrac{1}{{10}} + \dfrac{1}{8} - \dfrac{1}{5} = \dfrac{1}{{40}}\) (bể)

- Sử dụng công thức \(\dfrac{a}{{n\left( {n + a} \right)}} = \dfrac{1}{n} - \dfrac{1}{{n + a}}\) để rút gọn tổng ở vế trái

- Sử dụng quy tắc chuyển vế để tìm \(x\)

\(x + \dfrac{4}{{5.9}} + \dfrac{4}{{9.13}} + \dfrac{4}{{13.17}} + ... + \dfrac{4}{{41.45}} = \dfrac{{ - 37}}{{45}}\)

\(x + \dfrac{1}{5} - \dfrac{1}{9} + \dfrac{1}{9} - \dfrac{1}{{13}} + ... + \dfrac{1}{{41}} - \dfrac{1}{{45}} =  - \dfrac{{37}}{{45}}\)

\(x + \dfrac{1}{5} - \dfrac{1}{{45}} =  - \dfrac{{37}}{{45}}\)

\(x + \dfrac{8}{{45}} =  - \dfrac{{37}}{{45}}\)

\(x =  - \dfrac{{37}}{{45}} - \dfrac{8}{{45}}\)

\(x =  - 1\)

Vì \( - 1\) là số nguyên âm nên đáp án A đúng.

- Đánh giá từng số hạng của biểu thức: \(\dfrac{1}{{{n^2}}} < \dfrac{1}{{\left( {n - 1} \right).n}}\)

- Sử dụng công thức \(\dfrac{1}{{n\left( {n + 1} \right)}} = \dfrac{1}{n} - \dfrac{1}{{n + 1}}\)

\(P = \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + ... + \dfrac{1}{{{{2002}^2}}} + \dfrac{1}{{{{2003}^2}}}\)

\( < \dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + ... + \dfrac{1}{{2001.2002}} + \dfrac{1}{{2002.2003}}\)

\( = \dfrac{1}{1} - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + ... + \dfrac{1}{{2001}} - \dfrac{1}{{2002}} + \dfrac{1}{{2002}} - \dfrac{1}{{2003}}\)

\( = 1 - \dfrac{1}{{2003}} = \dfrac{{2002}}{{2003}} < 1\)

Vậy \(P < 1\)