Trắc nghiệm toán 6 các dạng toán bài 5 chương 1 cánh diều có đáp án — Không quảng cáo

Sử dụng các công thức ${a^m}.{a^n} = {a^{m + n}}$; ${a^m}:{a^n} = {a^{m - n}}$ $\left( {a \ne 0;\,m \ge n \ge 0} \right)$

+) Ta có ${5^2}{.5^3}{.5^4} = {5^{2 + 3 + 4}} = {5^9}$ nên A sai.

+) ${5^2}{.5^3}:{5^4} = {5^{2 + 3 - 4}} = {5^1} = 5$ nên B đúng

+) ${5^3}:5 = {5^{3 - 1}} = {5^2};\,{5^1} = 5$ nên C;D sai.

So sánh các lũy thừa bằng cách tính giá trị rồi so sánh.

Cách giải:

+) Ta có ${5^3} = 5.5.5 = 125$; ${3^5} = 3.3.3.3.3 = 243$ nên ${5^3} < {3^5}$ ( A đúng)

+) ${3^4} = 3.3.3.3 = 81$ và ${2^5} = 2.2.2.2.2 = 32$ nên ${3^4} > {2^5}$ ( B đúng)

+) ${4^3} = 4.4.4 = 64$ và ${2^6} = 2.2.2.2.2.2 = 64$ nên ${4^3} = {2^6}$ ( C đúng)

+) ${4^3} = 64;{8^2} = 64$ nên ${4^3} = {8^2}$ ( D sai)

Đưa hai vế về hai lũy thừa cùng số mũ rồi sử dụng ${a^n} = {a^m}\left( {a \ne 0;a \ne 1} \right)$ thì $n = m.$

Ta có  ${3^n} = 81$ mà $81 = {3^4}$ nên ${3^n} = {3^4}$ suy ra $n = 4.$

+ Sử dụng công thức ${a^m}.{a^n} = {a^{m + n}}$ để tính vế trái.

+ Sử dụng ${a^n} = {a^m}\left( {a \ne 0;a \ne 1} \right)$ thì $n = m.$

Ta có ${4^x} = {4^3}{.4^5}$

${4^x} = {4^{3 + 5}}$

${4^x} = {4^8}$

$x = 8$

Vậy $x = 8.$

+ So sánh các lũy thừa cùng cơ số : Nếu  ${a^m} > {a^n}$ thì $m > n.$

+ Từ đó chọn ra các giá trị thích hợp của $m.$

Ta có ${20^{2018}} < {20^m} < {20^{2020}}$ suy ra $2018 < m < 2020$ nên $m = 2019.$

+ So sánh các lũy thừa cùng cơ số : Nếu  ${a^m} > {a^n}$ thì $m > n.$

+ Từ đó chọn ra các giá trị thích hợp của $n.$

Vì ${5^2} < 90 < {5^3}$ nên từ ${5^n} < 90$ suy ra ${5^n} \le 5^2$

hay $n \le 2.$

Tức là $n = 0;1;2.$

Vậy có ba giá trị thỏa mãn.

Đưa về hai lũy thừa cùng số mũ rồi cho hai cơ số bằng nhau.

Ta có ${\left( {2x + 1} \right)^3} = 125$

${\left( {2x + 1} \right)^3} = {5^3}$

$2x + 1 = 5$

$2x = 5 - 1$

$2x = 4$

$x = 4:2$

$x = 2.$

+ Tìm số bị trừ ${2^x}$ bằng cách lấy hiệu cộng với số trừ.

+ Đưa về hai lũy thừa cùng cơ số và cho hai số mũ bằng nhau.

Ta có ${2^x} - 15 = 17$

${2^x} = 17 + 15$

${2^x} = 32$

${2^x} = {2^5}$

$x = 5.$

Vậy $x = 5 < 6.$

+ Tính vế phải

+ Đưa về hai lũy thừa cùng số mũ rồi cho hai cơ số bằng nhau

Ta có

${\left( {7x - 11} \right)^3} = {2^5}{.5^2} + 200$

${\left( {7x - 11} \right)^3} = 32.25 + 200$

${\left( {7x - 11} \right)^3} = 1000$

${\left( {7x - 11} \right)^3} = {10^3}$

$7x - 11 = 10$

$7x = 11 + 10$

$7x = 21$

$x = 21:7$

$x = 3.$

Vậy có $1$ số tự nhiên $x$ thỏa mãn đề bài là $x = 3.$

Vì ${0^m} = {0^n};\,{1^m} = {1^n}$ với mọi $m,n \ne 0$ nên

Xét các trường hợp:

+) $x - 4 = 0$

+) $x - 4 = 1$

Trường hợp 1: $x - 4 = 0$ suy ra $x = 4$ suy ra $x = 4.$

Trường hợp 2: $x - 4 = 1$ suy ra $x = 1 + 4$ hay $x = 5.$

Vậy tổng các số tự nhiên thỏa mãn là $4 + 5 = 9.$

+ Đưa ${16^{19}}$ và ${8^{25}}$ về lũy thừa cơ số $2$ (sử dụng công thức ${\left( {{a^m}} \right)^n} = {a^{m.n}}$ )

+ So sánh hai số mũ với nhau từ đó so sánh hai lũy thừa đã cho.

Ta có ${16^{19}}$$= {\left( {{2^4}} \right)^{19}} = {2^{4.19}} = {2^{76}}$

Và ${8^{25}} = {\left( {{2^3}} \right)^{25}} = {2^{75}}$

Mà $76 > 75$ nên ${2^{76}} > {2^{75}}$ hay ${16^{19}} > {8^{25}}.$

Sử dụng các công thức ${a^m}.{a^n} = {a^{m + n}};{a^m}:{a^n} = {a^{m - n}};\,$${\left( {{a^m}} \right)^n} = {a^{m.n}};\,{\left( {ab} \right)^m} = {a^m}.{b^m}\left( {a;b \ne 0,m \ge n} \right).$

Và tính chất $ab - ac = a\left( {b - c} \right).$

Ta có $A = \dfrac{{{{11.3}^{22}}{{.3}^7} - {9^{15}}}}{{{{\left( {{{2.3}^{13}}} \right)}^2}}}$$= \dfrac{{{{11.3}^{22 + 7}} - {{\left( {{3^2}} \right)}^{15}}}}{{{2^2}.{{\left( {{3^{13}}} \right)}^2}}}$$= \dfrac{{{{11.3}^{29}} - {3^{2.15}}}}{{{2^2}{{.3}^{13.2}}}}$$= \dfrac{{{{11.3}^{29}} - {3^{30}}}}{{{2^2}{{.3}^{26}}}}$$= \dfrac{{{{11.3}^{29}} - {3^{29}}.3}}{{{2^2}{{.3}^{26}}}}$

$= \dfrac{{{3^{29}}\left( {11 - 3} \right)}}{{{2^2}{{.3}^{26}}}} = \dfrac{{{3^{29}}.8}}{{{{4.3}^{26}}}} = {2.3^{29 - 26}} = {2.3^3} = 54.$

Vậy $A = 54.$

Biểu diễn số hạt thóc ở mỗi ô theo lũy thừa của 2.

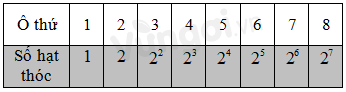
Vậy số hạt thóc ở ô thứ 8 là ${2^7}$ .

+ Tính $3A$ sau đó tính $2A = 3A - A$

+ Sử dụng điều kiện ở đề bài để đưa về dạng hai lũy thừa cùng cơ số. Cho hai số mũ bằng nhau ta tìm được $n.$

Ta có $A = 3 + {3^2} + {3^3} + ... + {3^{100}}\,\,\left( 1 \right)$ nên $3A = {3^2} + {3^3} + {3^4} + ... + {3^{100}} + {3^{101}}\,\,\left( 2 \right)$

Lấy $\left( 2 \right)$ trừ $\left( 1 \right)$ ta được $2A = {3^{101}} - 3$ do đó $2A + 3 = {3^{101}}$ mà theo đề bài $2A + 3 = {3^n}$

Suy ra ${3^n} = {3^{101}}$ nên $n = 101.$