Trắc nghiệm toán 6 các dạng toán bài 5,6 (tiếp) chương 2 cánh diều có đáp án — Không quảng cáo

Áp dụng tính chất nhân một số với \(0\): Số nào nhân với \(0\) cũng bằng \(0\)

Vì trong tích có một thừa số bằng \(0\) nên \(M = 0\)

Bước 1: Thu gọn biểu thức $A$ về dạng xuất hiện $a + b,x - y$ Bước 2: Thay $a + b,x - y$ vào biểu thức vừa thu gọn để tính.

$A = ax - ay + bx - by$ $ = (ax - ay) + (bx - by)$ $ = a.(x - y) + b.(x - y)$ $ = (a + b).(x - y)$

Thay $a + b =  - 5;x - y =  - 2$ ta được:

\(A = \left( { - 5} \right).\left( { - 2} \right) = 10\)

- Sử dụng quy tắc bỏ ngoặc.

- Nhóm \(x\) lại với nhau, nhóm số tự nhiên vào một nhóm.

- Áp dụng công thức tổng các số cách đều nhau:

Số số hạng = (Số cuối - số đầu):khoảng cách +1

Tổng = (Số cuối + số dầu).số số hạng :2

\(\begin{array}{l}\left( {x + 1} \right) + \left( {x + 2} \right) + ... + \left( {x + 99} \right) + \left( {x + 100} \right) = 0\\(x + x + .... + x) + (1 + 2 + ... + 100) = 0\\100{\rm{x}} + (100 + 1).100:2 = 0\\100{\rm{x}} + 5050 = 0\\100{\rm{x}} =  - 5050\\x =  - 50,5\end{array}\)

Mà \(x\in Z\) nên không có $x$ thỏa mãn.

Sử dụng khái niệm bội và ước của một số nguyên:

Nếu $a,b,x \in Z$ và $a = b.x$ thì $a \vdots b$ và $a$  là một bội của $b;b$ là một ước của $a$

Ta có: \( - 8 =  - 1.8 = 1.\left( { - 8} \right) =  - 2.4 = 2.\left( { - 4} \right)\)

Tập hợp các ước của \( - 8\) là: \(A = \left\{ {1; - 1;2; - 2;4; - 4;8; - 8} \right\}\)

+ Bước 1: Tìm ước của \(9\) + Bước 2: Tìm $a$ và kết luận giá trị lớn nhất của \(a\)

$a + 4$ là ước của $9$ $ \Rightarrow \;\left( {a + 4} \right) \in U\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\;$ Ta có bảng giá trị như sau:

Vậy giá trị lớn nhất của \(a\) là \(a = 5\)

Sử dụng tính chất chia hết trong tập hợp các số nguyên $a \, \vdots \, m;b \, \vdots \, m \Rightarrow (a + b) \, \vdots \, m$

Ta có:

\(\left( { - 154 + x} \right) \, \vdots \, 3\)

\(\left( { - 153 - 1 + x} \right) \, \vdots \, 3\)

Suy ra \(\left( {x - 1} \right) \, \vdots \, 3\) (do \( - 153 \, \vdots \, 3\))

Do đó \(x - 1 = 3k \Rightarrow x = 3k + 1\)

Vậy \(x\) chia cho \(3\) dư \(1.\)

Bước 1: Phân tích $n + 5$  về dạng $a.\left( {n + 1} \right) + b{\rm{ }}\left( {a,b\; \in \;Z,a \ne 0} \right)$ Bước 2: Tìm $n$

$\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$$ \Rightarrow \left( {n + 1} \right) + 4 \, \vdots \,  \left( {n{\rm{ }} + 1} \right)$

Vì \(n + 1 \, \vdots \, n + 1\) và \(n \in Z\) nên để \(n + 5 \, \vdots \, n + 1\) thì \(4 \, \vdots \, n + 1\)

Hay \(n + 1 \in U\left( 4 \right) = \left\{ { \pm 1; \pm 2; \pm 4} \right\}\)

Ta có bảng:

Vậy \(n \in \left\{ { - 5; - 3; - 2;0;1;3} \right\}\)

\(10\) là bội của \(2a + 5\) nghĩa là \(2a + 5\) là ước của \(10\)

- Tìm các ước của \(10\)

- Lập bảng tìm \(a,\) đối chiếu điều kiện và kết luận.

Vì \(10\) là bội của \(2a + 5\) nên \(2a + 5\) là ước của \(10\)

\(U\left( {10} \right) = \left\{ { \pm 1; \pm 2; \pm 5; \pm 10} \right\}\)

Ta có bảng:

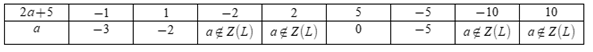
Mà \(a < 5\) nên \(a \in \left\{ { - 3; - 2;0; - 5} \right\}\)

Vậy có \(4\) giá trị nguyên của \(a\) thỏa mãn bài toán.

Sử dụng định nghĩa chia hết: \(a \, \vdots \, b\) nếu và chỉ nếu tồn tại số \(q \in Z\) sao cho \(a = b.q\)

Ta có:

\(\begin{array}{l}a \, \vdots \, b \Rightarrow a = b.{q_1}\left( {{q_1} \in Z} \right)\\b \, \vdots \, a \Rightarrow b = a.{q_2}\left( {{q_2} \in Z} \right)\end{array}\)

Suy ra \(a = b.{q_1} = \left( {a.{q_2}} \right).{q_1} = a.\left( {{q_1}{q_2}} \right)\)

Vì \(a \ne 0\) nên \(a = a\left( {{q_1}{q_2}} \right) \Rightarrow 1 = {q_1}{q_2}\)

Mà \({q_1},{q_2} \in Z\) nên \({q_1} = {q_2} = 1\) hoặc \({q_1} = {q_2} =  - 1\)

Do đó \(a = b\) hoặc \(a =  - b\)

Biến đổi biểu thức \({n^2} - 7\) về dạng \(a.\left( {n + 3} \right) + b\) với \(b \in Z\) rồi suy ra \(n + 3\) là ước của \(b\)

Ta có:\({n^2} - 7 = {n^2} + 3n - 3n - 9 + 2\)\( = n\left( {n + 3} \right) - 3\left( {n + 3} \right) + 2\)\( = \left( {n - 3} \right)\left( {n + 3} \right) + 2\)

Vì \(n \in Z\) nên để \({n^2} - 7\) là bội của \(n + 3\) thì \(2\) là bội của \(n + 3\) hay \(n + 3\) là ước của \(2\)

\(Ư\left( 2 \right) = \left\{ { \pm 1; \pm 2} \right\}\) nên \(n + 3 \in \left\{ { \pm 1; \pm 2} \right\}\)

Ta có bảng:

Vậy \(n \in A = \left\{ { - 5; - 4; - 2; - 1} \right\}\)

Do đó tổng các phần tử của \(A\) là \(\left( { - 5} \right) + \left( { - 4} \right) + \left( { - 2} \right) + \left( { - 1} \right) =  - 12\)

+ Biến đổi để tách \(5x + 46y\) thành tổng của hai số, trong đó một số chia hết cho $16$  và một số chứa nhân tử \(x + 6y\)

+ Sử dụng tính chất chia hết trên tập hợp các số nguyên để chứng minh.

Ta có:

\(\begin{array}{l}5x + 46y = 5x + 30y + 16y\\ = \left( {5x + 30y} \right) + 16y\\ = 5\left( {x + 6y} \right) + 16y\end{array}\)

Vì \(5x + 46y\) chia hết cho $16$  và $16y$ chia hết cho $16$ nên suy ra \(5\left( {x + 6y} \right)\) chia hết cho $16.$

Mà $5$  không chia hết cho $16$ nên suy ra \(x + 6y\) chia hết cho $16$

Vậy nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) cũng chia hết cho $16.$

Áp dụng: \(b\) chia hết cho \(a\) và \(a\) chia hết cho \(b\) thì \(a\),\(b\) là hai số đối nhau (đã chứng minh từ bài tập trước), từ đó suy ra \(n\).

Vì \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(n - 1\),

Nên \(n - 1\) khác \(0\) và \(n + 5\) khác \(0\)

Nên \(n + 5,n - 1\) là hai số đối nhau

Do đó:

\((n + 5) + (n - 1) = 0\)

\(2n + 5 - 1 = 0\)

\(2n + 4 = 0\)

\(2n = -4\)

\(n=-2\)

Vậy có 1 số nguyên n thỏa mãn bài toán.