Trắc nghiệm toán 8 bài 1 chương 2 chân trời sáng tạo có đáp án — Không quảng cáo

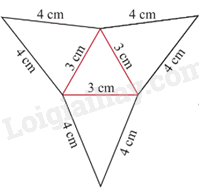
Dựa vào cách tạo lập hình chóp tứ giác đều.

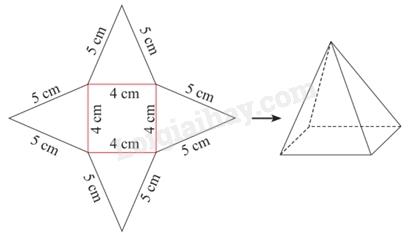
Khi gập lại ta thấy độ dài cạnh bên bằng 5cm

Sử dụng kiến thức về hình chóp tam giác đều.

Hình chóp tam giác đều có 6 cạnh, nên cần 6 que diêm để xếp thành hình chóp tam giác đều.

Sử dụng kiến thức về các cạnh của hình chóp tứ giác đều: Hình chóp tứ giác đều có đáy là hình vuông, các mặt bên là các tam giác cân bằng nhau có chung đỉnh.

Hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông nên \(AB = BC = CD = DA = 6cm\)

Khi đó chu vi mặt đáy ABCD là: \(C = 6.4 = 24cm\)nên chọn đáp án C đúng

Sử dụng kiến thức về hình chóp đều, độ dài trung đoạn để tính.

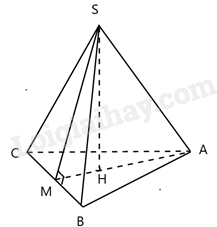
Hình chóp tam giác đều S.ABC có tất cả các cạnh bằng nhau \( \Rightarrow SA = SB = SC = AB = AC = BC\).

Gọi H là trọng tâm tam giác ABC đều , M là trung điểm BC.

Theo định nghĩa trung đoạn, SM là trung đoạn của hình chóp.

Đáy ABC là tam giác đều \( \Rightarrow \)AM vừa là trung tuyến vừa là đường cao\( \Rightarrow AM \bot BC \Rightarrow \widehat {AMB} = {90^0} \Rightarrow \Delta AMB\)vuông tại M.

\(AM = 3\sqrt 3 cm\)

Ta có: \(SA = SB = SC \Rightarrow \Delta SAB\)đều\( \Rightarrow \) SM vừa là trung tuyến vừa là đường cao.\( \Rightarrow SM \bot BC \Rightarrow \widehat {SMB} = {90^0} \Rightarrow \Delta SMB\) vuông tại M

Xét tam giác vuông SMB và tam giác vuông AMB có:

MB chung

SB = AB

\( \Rightarrow \Delta SMB = \Delta AMB\)(cạnh huyền – cạnh góc vuông)

\( \Rightarrow SM = AM = 3\sqrt 3 (cm)\)

Vậy chiều cao mặt bên hình chóp SM bằng \(3\sqrt 3 cm\)

Sử dụng kiến thức về hình chóp đều, chứng minh hai tam giác bằng nhau để so sánh.

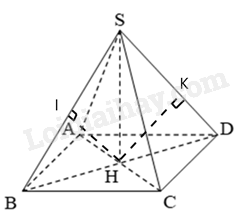
Hình chóp tứ giác đều S.ABC có tất cả các cạnh bằng nhau \( \Rightarrow SA = SB = SC = SD = AB = AC = BC = CD\).

Kẻ HI và HK lần lượt vuông góc với SB và SD . Khi đó: \({d_1} = HI,{d_2} = HK\)

Xẻ mặt đáy hình chóp là một hình vuông như hình dưới:

Xét tam giác ABH và tam giác CDH có:

AB = CD (ABCD là hình vuông)

\({\widehat B_1} = {\widehat D_1}\) (2 góc so le trong)

SB = AB

\( \Rightarrow \Delta AHB = \Delta CHD(g.c.g)\)

\( \Rightarrow BH = DH\)(2 cạnh tương ứng)

Xét tam giác SBH và tam giác SHD có:

SB = SD

SH chung

HB = HD ( chứng minh trên)

\( \Rightarrow \Delta SHB = \Delta SHD(c.c.c)\)

\( \Rightarrow \widehat {SBH} = \widehat {SDH}\) (2 góc tương ứng) hay \(\widehat {IBH} = \widehat {KDH}\)

Xét tam giác vuông IHB và tam giác vuông KHD có:

\(\widehat {IBH} = \widehat {KDH}\)

HB = HD ( chứng minh trên)

\( \Rightarrow \Delta IHB = \Delta KHD\)(cạnh huyền – góc nhọn)

\(\begin{array}{l} \Rightarrow IH = KH\\ \Rightarrow {d_1} = {d_2}\end{array}\)

Sử dụng định nghĩa hình chóp tam giác đều: Hình chóp tam giác đều có đáy là tam giác đều, các mặt bên là các tam giác cân bằng nhau có chung đỉnh.

Theo định nghĩa hình chóp tam giác đều, mặt đáy là các tam giác đều nên chọn đáp án D

Sử dụng định nghĩa đường cao của hình chóp tứ giác đều: Đoạn thẳng nối đỉnh của hình chóp và giao của hai đường chéo gọi là đường cao của hình chóp tứ giác đều

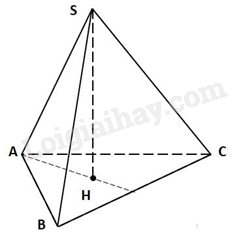
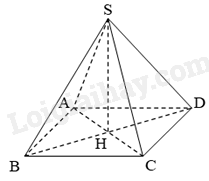
Theo định nghĩa đường cao của hình chóp tứ giác đều thì đường cao là đoạn thẳng nối từ đỉnh tới giao của hai đường chéo của mặt đáy nên SO là đường cao của hình chóp nên chọn đáp án A

Quan sát hình chóp tam giác đều, đếm số mặt.

Hình chóp tam giác có 4 mặt bao gồm 3 mặt bên và 1 mặt đáy.

Sử dụng định nghĩa hình chóp tứ giác đều: Hình chóp tứ giác đều có đáy là hình vuông, các mặt bên là các tam giác cân bằng nhau có chung đỉnh.

Theo định nghĩa hình chóp tứ giác đều, các mặt bên là các tam giác cân nên chọn đáp án B

Sử dụng định nghĩa của hình chóp tam giác đều.

Theo định nghĩa hình chóp tam giác đều thì mặt đáy của hình chóp SABC là mặt ABC

Quan sát hình chóp tam giác đều đếm số cạnh bên.

Hình chóp tam giác đều có 4 cạnh bên nên chọn đáp án B

Sử dụng khái niệm đường cao của hình chóp tam giác đều

Theo khái niệm đường cao của hình chóp tam giác đều thì đường cao của hình chóp S.ABC là đoạn SO nên chọn đáp án B

Sử dụng kiến thức đáy của hình chóp tam giác đều là tam giác đều.

Vì đáy của hình chóp tam giác đều là tam giác đều, mà mỗi góc của tam giác đều có số đo bằng \({60^0}\) nên chọn đáp án C

Sử dụng kiến thức về các cạnh của hình chóp tam giác đều: Hình chóp tam giác đều có đáy là tam giác đều, các mặt bên là các tam giác cân bằng nhau có chung đỉnh.

Hình chóp tam giác đều có các mặt bên là các tam giác cân bằng nhau có chung đỉnh nên độ dài các cạnh bên luôn bằng nhau nên chọn đáp án A đúng.

Sử dụng khái niệm hình chóp tam giác đều, hình chóp tứ giác đều

Hình chóp tứ giác đều có các cạnh bên bằng nhau và đáy là hình vuông nên đáp án B sai.

Dựa vào đặc điểm của hình chóp tam giác đều.

Hình chóp tam giác đều có các mặt bên là các tam giác cân bằng nhau có chung đỉnh nên \(SB = SC = SA = 4cm\) .

Sử dụng định nghĩa hình chóp tam giác đều, hình chóp tứ giác đều.

Sử dụng định nghĩa hình chóp tam giác đều, hình chóp tứ giác đều ta thấy các cạnh bên bằng nhau, đáy của hình trên là tam giác đều nên chọn đáp án B

Dựa vào đặc điểm của hình chóp tam giác, tứ giác đều.

Vì hình chóp có số cạnh gấp đôi số cạnh của đa giác ở đáy nên hình chóp có 8 cạnh thì đa giác đáy có 8 : 2 = 4 cạnh. Hay đáy là tứ giác đều. Vậy đây là hình chóp tứ giác đều

Dựa vào đặc điểm của hình chóp tứ giác đều.

Hình chóp tứ giác đều có 1 đỉnh, 8 cạnh và 5 mặt.

Dựa vào khái niệm hình chóp tam giác đều

Hình 1: Khi gấp lại, ta gấp được hình chóp tam giác đều vì có ba mặt bên và đáy là tam giác đều.

Hình 2: Khi gấp lại, hình chóp không đều vì thừa nhiều mặt.

Hình 3: Khi gấp lại, không được hình chóp tam giác đều vì thừa một mặt.

Vậy chọn đáp án B

Dựa vào khái niệm hình chóp tam giác đều,hình chóp tứ giác đều.

Hình chóp tam giác đều có đáy là tam giác đều, các mặt bên là các tam giác cân bằng nhau có chung đỉnh nên câu A sai

Dựa vào công thức tính chu vi hình vuông và định nghĩa hình chóp tứ giác.

Hình chóp tứ giác đều có đáy là hình vuông, tất cả các cạnh đều bằng nhau nên cạnh bên tăng lên hai lần thì cạnh đáy tăng hai lần. Khi đó chu vi hình vuông cũng tăng lên 2 lần.

Sử dụng kiến thức về các cạnh của hình chóp tam giác đều: Hình chóp tam giác đều có đáy là tam giác đều, các mặt bên là các tam giác cân bằng nhau có chung đỉnh.

Hình chóp tam giác đều S.ABC có đáy ABC là tam giác đều nên \(AC = BC = AB = 3cm\)

Hình chóp tam giác đều có các mặt bên là các tam giác cân bằng nhau có chung đỉnh nên \(SB = SC = SA = 4cm\).

nên chọn đáp án B đúng

Sử dụng kiến thức về các cạnh của hình chóp tam giác đều: Hình chóp tam giác đều có đáy là tam giác đều, các mặt bên là các tam giác cân bằng nhau có chung đỉnh.

Hình chóp tam giác đều A.BCD có đáy BCD là tam giác đều nên \(BD = BC = BD = 5cm\)

Hình chóp tam giác đều có các mặt bên là các tam giác cân bằng nhau có chung đỉnh nên \(AC = AD = AB = 3cm\)

Vậy chọn đáp án B.

Sử dụng kiến thức về hình chóp tứ giác đều.

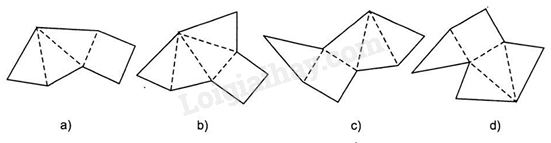
Hình a khi gấp lại thì không được một hình chóp đều vì đáy là tứ giác đều nhưng chỉ có ba mặt bên thay vì phải có 4 mặt bên.

Hình b, c khi gấp lại thì được một hình chóp tứ giác đều.

Hình d khi gấp lại thì không đượ c một hình chóp tứ giác đều vì ở trên cùng một cạnh đáy có đến 2 mặt bên còn trên một cạnh đáy thì không có mặt bên nào.