Bài 19 trang 75 SGK Toán 9 tập 2
Cho một đường tròn tâm O
Đề bài
Cho một đường tròn tâm \(O\), đường kính \(AB\) và \(S\) là một điểm nằm ngoài đường tròn. \(SA\) và \(SB\) lần lượt cắt đường tròn tại \(M, N\). Gọi \(H\) là giao điểm của \(BM\) và \(AN\). Chứng minh rằng \(SH\) vuông góc với \(AB\).
Phương pháp giải - Xem chi tiết
Sử dụng góc nội tiếp chắn nửa đường tròn là góc vuông để chỉ ra các đường cao của tam giác \(SAB.\)
Sử dụng tính chất trực tâm để suy ra \(SH \bot AB.\)
Lời giải chi tiết
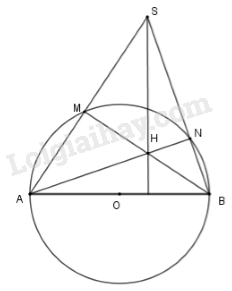
Xét đường tròn tâm \(O\) có \(AB\) là đường kính nên \(\widehat {AMB} = \widehat {ANB} = 90^\circ \) ( góc nội tiếp chắn nửa đường tròn)
Suy ra \(BM \bot SA;\,AN \bot SB\) mà \(BM \cap AN\) tại \(H\) nên \(H\) là trực tâm tam giác \(SAB.\)
Do đó \(SH \bot AB.\) (vì trong một tam giác ba đường cao đồng quy)