Bài 23 trang 76 SGK Toán 9 tập 2
Cho đường tròn (O)
Đề bài
Cho đường tròn \((O)\) và một điểm \(M\) cố định không nằm trên đường tròn. Qua \(M\) kẻ hai đường thẳng. Đường thẳng thứ nhất cắt \((O)\) tại \(A\) và \(B\).Đường thẳng thứ nhất cắt \((O)\) tại \(C\) và \(D\).
Chứng minh \(MA. MB = MC. MD\)
Phương pháp giải - Xem chi tiết
Sử dụng tam giác đồng dạng để suy ra hệ thức cần chứng minh
Lời giải chi tiết
Xét hai trường hợp:
a) \(M\) ở bên trong đường tròn (hình a)
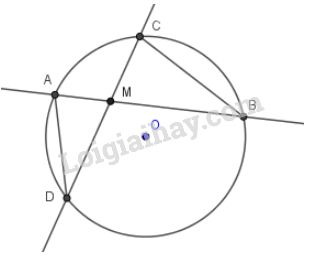
Xét hai tam giác \(MAD\) và \(MCB\) có:
\(\widehat{AMD}\) = \(\widehat{CMB}\) ( đối đỉnh)
\(\widehat{ADM}\) = \(\widehat{CBM}\) (hai góc nội tiếp cùng chắn cung \(AC\)).
Do đó \(∆MAD\) đồng dạng \(∆MCB\) (g-g), suy ra:
\(\dfrac{MA}{MC}=\dfrac{MD}{MB}\) ( 2 cặp cạnh tương ứng tỉ lệ).
Do đó \(MA. MB = MC. MD\)
b) M ở bên ngoài đường tròn (hình b)
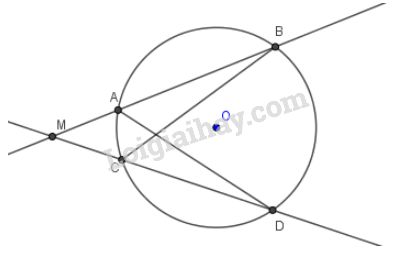
Tương tự, x ét hai tam giác \(MAD\) và \(MCB\) có:
\(\widehat{M}\) chung
\(\widehat{MDA}\) = \(\widehat{MBC}\) (hai góc nội tiếp cùng chắn cung \(AC\)).
Nên \(∆MAD\) đồng dạng \(∆MCB\) (g-g)
Suy ra: \(\dfrac{MA}{MC}=\dfrac{MD}{MB}\) ( 2 cặp cạnh tương ứng tỉ lệ).
Do đó: \(MA. MB = MC. MD\)