Bài 24 trang 15 SGK Toán 9 tập 1 — Không quảng cáo

Đề bài

Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ $3$) của các căn thức sau:

$a)$ $\sqrt{4(1 + 6x + 9x^{2})^{2}}$ tại $x =  - \sqrt 2$;

$b)$ $\sqrt{9a^{2}(b^{2} + 4 - 4b)}$ tại $a =  - 2;\,\,b =  - \sqrt 3$.

Lời giải chi tiết

a) Ta có:

$\sqrt{4(1 + 6x + 9x^{2})^{2}}$ $=\sqrt {4}. \sqrt {{{(1 + 6x + 9{x^2})}^2}}$

$=\sqrt{4}.\sqrt{(1+2.3x+3^2.x^2)^2}$

$=\sqrt{2^2}.\sqrt{\left[1^2+2.3x+(3x)^2\right]^2}$

$=2.\sqrt {{{\left[ {{{\left( {1 + 3x} \right)}^2}} \right]}^2}}$

$=2.\left|(1+3x)^2\right|$

$=2(1+3x)^2$.

(Vì  $(1+3x)^2 > 0$ với mọi $x$  nên $\left|(1+3x)^2\right|=(1+3x)^2$)

Thay $x =  - \sqrt 2$ vào biểu thức rút gọn trên, ta được:

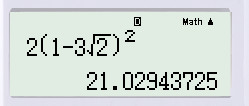
$2{\left[ {1 + 3.(-\sqrt 2) } \right]^2}=2(1-3\sqrt{2})^2$.

Bấm máy tính, ta được: $2{\left( {1 - 3\sqrt 2 } \right)^2} \approx 21,029$.

b) Ta có:

$\sqrt{9a^{2}(b^{2} + 4 - 4b)} =\sqrt{3^2.a^2.(b^2-4b+4)}$

$=\sqrt{(3a)^2.(b^2-2.b.2+2^2)}$

$=\sqrt{(3a)^2}. \sqrt{(b-2)^2}$

$=\left|3a\right|. \left|b-2\right|$

Thay $a = -2$ và $b =  - \sqrt 3$ vào biểu thức rút gọn trên, ta được:

$\left| 3.(-2)\right|. \left| -\sqrt{3}-2\right| =\left|-6\right|.\left|-(\sqrt{3}+2) \right|$

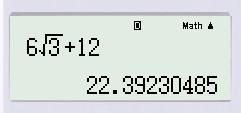
$=6.(\sqrt{3}+2)=6\sqrt{3}+12$.

Bấm máy tính, ta được: $6\sqrt{3}+12 \approx 22,392$.