Bài 23 trang 119 SGK Toán 9 tập 2 — Không quảng cáo

Đề bài

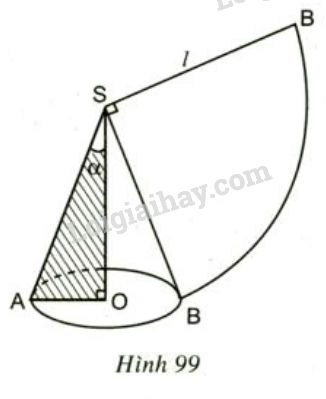
Viết công thức tính nửa góc ở đỉnh của một hình nón (góc $\alpha$ của tam giác vuông $AOS$- hình 99) sao cho diện tích khai triển mặt nón bằng một phần tư diện tích hình tròn (bán kính $SA$).

Lời giải chi tiết

Diện tích hình quạt : $S_{quạt} = \dfrac{\pi r^2 n^o}{360^o}= \dfrac{\pi.l^2.90}{360}=\dfrac{\pi.l^2}4.$

Diện tích xung quanh của hình nón: ${S_{xq}} = \pi rl$

Theo đề bài ta có: ${S_{xq}} = S_{quạt} \Rightarrow πrl= \dfrac{\pi.l^2}4$$\Rightarrow$ $l = 4r.$

Trong tam giác vuông SOA, ta có: $\sin \alpha =\dfrac {OA}{SA}= \dfrac{r}l = \dfrac {1}4$ (vì $l=4r$.)

Vậy $\alpha= {14^0}28'.$