Bài 27 trang 119 SGK Toán 9 tập 2

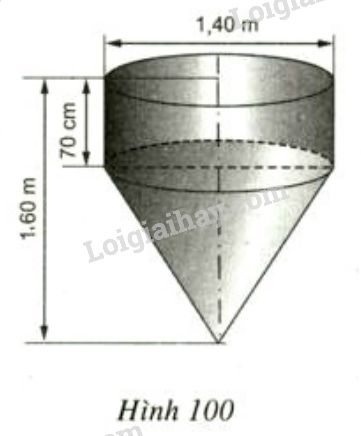
Một phần dụng cụ gồm một phần có dạng trụ, phần còn lại có dạng nón. Các kích thước cho trên hình 100. Hãy tính:

Đề bài

Một phần dụng cụ gồm một phần có dạng trụ, phần còn lại có dạng nón. Các kích thước cho trên hình 100. Hãy tính:

a) Thể tích của dụng cụ này;

b) Diện tích mặt ngoài của dụng cụ (Không tính nắp đậy).

Phương pháp giải - Xem chi tiết

+) Diện tích xung quanh hình trụ: $S_{xq \, \, trụ}= 2\pi rh.$

+) Diện tích xung quanh hình nón: $S_{xq \, \, nón}= \pi rl.$

+) Thể tích hình trụ: $V_{trụ}=\pi r^2h.$

+) Thể tích hình nón: $V_{nón}=\dfrac{1}{3} \pi r^2h.$

Lời giải chi tiết

Lấy $\pi=3,14$

a) Thể tích cần tính gồm một hình trụ, đường kính đáy $1,4m$ nên bán kính đáy là $\frac{1,4}{2}$ = 0,7 m, chiều cao $70cm=0,7m$ , và một hình nón, bán kính đáy bằng bán kính hình trụ, chiều cao hình nón bằng $0,9m$ .

Thể tích hình trụ:

$V_{trụ}$ $\displaystyle =\pi {R^2}h = 3,14.0,7^2.0,7=1,077({m^3}).$

Thể tích hình nón:

$\displaystyle V_{nón}={1 \over 3}.3,14.0,7^2.0,9 = 0,462({m^3}).$

Vậy thể tích cái phễu:

$V =V_{trụ}+ V_{nón}$ $=1,077+0,462=1,539({m^3}).$

b) Diện tích cần tính = diện tích xung quanh hình trụ + diện tích xung quanh hình nón.

Đường sinh của hình nón là:

$l = \sqrt{h^2 + r^2}=\sqrt{0,9^2+0,7^2}= \sqrt{1,3}$ $\approx 1,14(m)$

$\displaystyle S_{xq \, \, trụ}= 2\pi rh = 2.3,14.0,7.0,7 = 3,077({m^2})$

$S_{xq \, \, nón}$ $=\displaystyle \pi rl = 3,14.0,7.1,4 = 2,506({m^2})$

Vậy diện tích toàn phần của phễu: