Bài 3 trang 134 SGK Toán 9 tập 2
Cho tam giác ABC vuông ở C có đường trung tuyến BN vuông góc với đường trung tuyến CM, cạnh BC = a. Tính độ dài đường trung tuyến BN.
Đề bài
Cho tam giác \(ABC\) vuông ở \(C\) có đường trung tuyến \(BN\) vuông góc với đường trung tuyến \(CM,\) cạnh \(BC = a.\) Tính độ dài đường trung tuyến \(BN.\)
Phương pháp giải - Xem chi tiết
Áp dụng công thức hệ thức lượng trong tam giác vuông và định lý Pi-ta-go.
Lời giải chi tiết
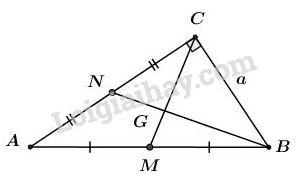
Gọi \(G\) là trọng tâm của tam giác \(ABC,\) ta có: \(\displaystyle BG = {2 \over 3}BN.\)
Áp dụng hệ thức lượng trong tam giác vuông \(CNB\) có đường cao \(CG\) ta có:
\(\eqalign{ & B{C^2} = BN.BG = BN.{2 \over 3}BN = {2 \over 3}B{N^2} \cr & \Rightarrow B{N^2} = {3 \over 2}B{C^2} = {{3{a^2}} \over 2} \cr & \Rightarrow BN = \sqrt {{{3{{\rm{a}}^2}} \over 2}} = {{a\sqrt 3 } \over {\sqrt 2 }} = {{a\sqrt 6 } \over 2}. \cr}\)
Vậy \(\displaystyle BN = {{a\sqrt 6 } \over 2}.\)