Bài 32 trang 89 SGK Toán 9 tập 1 — Không quảng cáo

Đề bài

Một con thuyền với vận tốc $2km/h$ vượt qua một khúc sông nước chảy mạnh mất $5$ phút. Biết rằng đường đi của con thuyền tạo với bờ một góc $70^{\circ}$. Từ đó đã có thể tính được chiều rộng của khúc sông chưa? Nếu có thể hãy tính kết quả (làm tròn đến mét).

Lời giải chi tiết

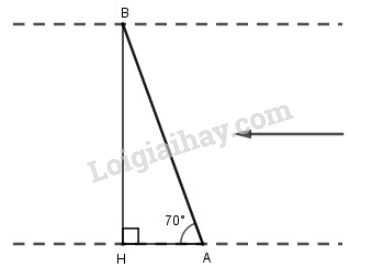
Gọi $AB$ là đoạn đường mà con thuyền đi được trong $5$ phút, $BH$ là chiều rộng của khúc sông.

Đổi $5$ phút $=\dfrac{1}{12}h.$ Biết vận tốc của thuyền là $v=2km/h$

Suy ra quãng đường thuyền đi trong $5$ phút là: $AB=S=v.t=2.\dfrac{1}{12}=\dfrac{1}{6}$  (km).

Xét tam giác $HAB$ vuông tại $H$, $AB=\dfrac{1}{6}km,\ \widehat{A}=70^o$, ta có:

$BH=AB. \sin A = \dfrac{1}{6}. \sin 70^o$$\approx 0,1566(km)=156,6m$

Vậy chiều rộng khúc sông xấp xỉ $156,6(m)$.