Bài 4 trang 100 SGK Toán 9 tập 1
Trên mặt phẳng tọa độ Oxy, hãy xác định vị trí của mỗi điểm A(-1;-1), B(-1;-2),
Đề bài
Trên mặt phẳng tọa độ \(Oxy\), hãy xác định vị trí của mỗi điểm \(A(-1;-1),\ B(-1;-2),\ C(\sqrt{2};\sqrt{2})\) đối với đường tròn tâm \(O\) bán kính \(2\).
Phương pháp giải - Xem chi tiết
+) Khoảng cách d từ gốc tọa độ \(O(0; 0)\) đến điểm \(A(x;y)\) được tính theo công thức \(d=\sqrt{x^{2}+y^{2}}\). (1)
+) Cho đường tròn tâm \(O\) bán kính \(R\), khi đó:
a) Nếu \(OM=R\) thì \(M\) nằm trên đường tròn.
b) Nếu \(OM > R\) thì \(M\) nằm ngoài đường tròn.
c) Nếu \(OM < R\) thì \(M\) nằm trong đường tròn.
Lời giải chi tiết
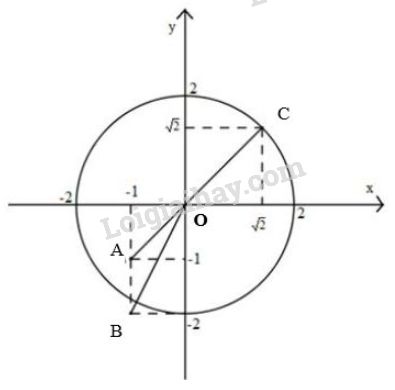
Áp dụng công thức (1) tính khoảng cách từ một điểm đến gốc tọa độ , ta có:
\(OA=\sqrt {{{( - 1)}^2} + {{( - 1)}^2}} =\sqrt{2}< 2\Rightarrow A\) nằm trong đường tròn \((O;2)\).
\(OB=\sqrt {{{( - 1)}^2} + {{( - 2)}^2}} =\sqrt{5}> 2\Rightarrow B\) nằm ngoài đường tròn \((O;2)\).
\(OC=\sqrt {{{\left( {\sqrt 2 } \right)}^2} + {{\left( {\sqrt 2 } \right)}^2}} =2\Rightarrow C\) nằm trên đường tròn \((O;2)\).