Bài 5 trang 40 SGK Toán 11 tập 1 - Cánh diều
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu.
Đề bài
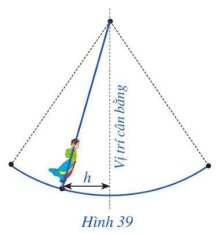
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (Hình 39). Nghiên cứu trò chơi này, người ta thấy khoảng cách h (m) từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian t (s) (với \(t \ge 0\)) bởi hệ thức \(h = \left| d \right|\) với \(d = 3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]\), trong đó ta quy ước d > 0 khi vị trí cân bằng ở phía sau lưng người chơi đu và d < 0 trong trường hợp ngược lại. Vào thời gian t nào thì khoảng cách h là 3m; 0m?
Phương pháp giải - Xem chi tiết
Sử dụng công thức tổng quát để giải phương trình hàm số cos.
Lời giải chi tiết
+) Khi khoảng cách từ người chơi đu đến vị trí cân bằng là 3m thì h = 3.
Khi đó
\(\begin{array}{l}3 = \left| d \right| = \left| {3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]} \right|\\ \Rightarrow \left[ \begin{array}{l}3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 3\\3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = - 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 1\\\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = - 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \cos 0\\\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \cos \pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{3}\left( {2t - 1} \right) = k2\pi \\\frac{\pi }{3}\left( {2t - 1} \right) = \pi + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{{6k + 1}}{2}\\t = 3k + 2\end{array} \right.;k \in Z\end{array}\)
+) Khi khoảng cách từ người chơi đu đến vị trí cân bằng là 0m thì h = 0.
Khi đó
\(\begin{array}{l}0 = \left| d \right| = \left| {3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]} \right|\\ \Rightarrow 3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \cos \frac{\pi }{2}\\ \Leftrightarrow \frac{\pi }{3}\left( {2t - 1} \right) = \frac{\pi }{2} + k\pi \\ \Leftrightarrow t = \frac{5}{4} + \frac{{3k}}{2};k \in Z\end{array}\)