Bài 8. 11 trang 63 SGK Toán 11 tập 2 - Cùng khám phá — Không quảng cáo

Đề bài

Cho hình chóp S.ABC có đáy  ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S trên (ABC) trùng với trung điểm H của cạnh BC và SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC).

Lời giải chi tiết

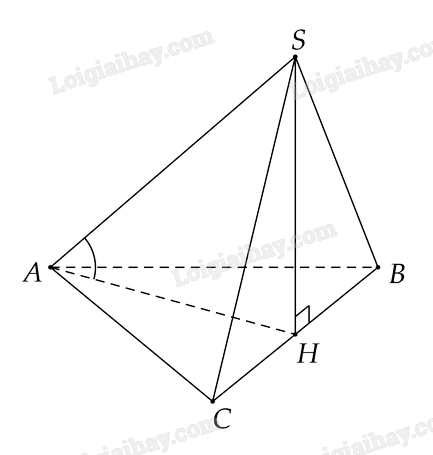
Vì hình chiếu vuông góc của $S$ trên $\left( {ABC} \right)$ là trung điểm $H$ của $BC$ nên $SH \bot \left( {ABC} \right)$

Vì $SH \bot \left( {ABC} \right)$ nên $AH$ là hình chiếu vuông góc của $SA$ trên $\left( {ABC} \right)$

Vậy góc giữa $SA$ và $\left( {ABC} \right)$ là góc giữa $SA$ và $AH$, góc giữa $SA$ và $AH$ là góc $\widehat {SAH}$

Vì $\Delta ABC$ là tam giác đều cạnh $a$ suy ra đường trung tuyến $AH$ nên $AH = \frac{{a\sqrt 3 }}{2}$

Vì $\Delta SBC$ là tam giác đều có cạnh $BC = a$ suy ra đường trung tuyến $SH = \frac{{a\sqrt 3 }}{2}$

Xét $\Delta SAH$ vuông tại $A$ có $\tan \widehat {SAH} = \frac{{SH}}{{AH}} = \frac{{a\sqrt 3 }}{2}:\frac{{a\sqrt 3 }}{2} = 1$$\Rightarrow \widehat {SAH} = {45^o}$