Bài 8 trang 134 SGK Toán 9 tập 2
Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài (R > r).
Đề bài
Cho hai đường tròn \((O; R)\) và \((O'; r)\) tiếp xúc ngoài \((R > r).\) Hai tiếp tuyến chung \(AB\) và \(A'B'\) của hai đường tròn \((O)\) và \((O')\) cắt nhau tại \(P\) (\(A\) và \(A'\) thuộc đường tròn \((O'),\) \(B\) và \(B'\) thuộc đường tròn \((O)\)). Biết \(PA = AB = 4 cm.\) Tính diện tích hình tròn \((O').\)
Phương pháp giải - Xem chi tiết
+) Sử dụng định lý Ta-lét để tính \(PO'\) theo \(r\)
+) Sử dụng định lý Pytago cho tam giác vuông \(PO'A\) để tính \({r^2}.\)
+) Diện tích hình tròn \(\left( {O'} \right)\) là \(S = \pi {r^2}.\)
Lời giải chi tiết
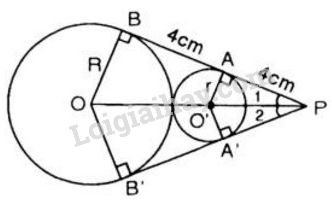
Vì \(AB\) là tiếp tuyến chung của \((O)\) và \((O’)\) nên \(OB \bot AB\) và \(O’A \bot AB\)
Xét hai tam giác \(OPB\) và \(O’AP\), ta có:
\(\widehat A = \widehat B = {90^0}\)
\(\widehat {{P_1}}\) chung
Vậy \(ΔOBP \backsim ∆ O’AP (g-g)\)
\(\eqalign{ & \Rightarrow {r \over R} = {{PO'} \over {PO}} = {{PA} \over {PB}} = {4 \over 8} = {1 \over 2} \cr & \Rightarrow R = 2{\rm{r}} \cr} \)
Xét tam giác OBP có:
O'A // OB ( cùng vuông góc với BP)
AB = AP
\(\Rightarrow\) O'A là đường trung bình của \(∆OBP\))
\(\Rightarrow OO' = O'P=R + r = 3r\)
Áp dụng định lí Py-ta-go trong tam giác vuông \(O’AP\)
\(O’P^2 = O’A^2 + AP^2\) hay \({\left( {3r} \right)^2} = {\rm{ }}{r^2} + {\rm{ }}{4^{2}} \Leftrightarrow {\rm{ }}9{r^2} = {\rm{ }}{r^2} + {\rm{ }}16{\rm{ }}\)
\( \Leftrightarrow {\rm{ }}8{\rm{ }}{r^2} = 16{\rm{ }} \Leftrightarrow {\rm{ }}{r^2} = {\rm{ }}2\)
Diện tích đường tròn \((O’;r)\) là:
\(S = π. r^2 = π.2 = 2π\) (\(cm^2\))