Câu 1 trang 120 SGK Hình học 11 Nâng cao
Tứ diện OABC có OA = OB = OC = a và
Đề bài
Tứ diện OABC có OA = OB = OC = a và \(\widehat {AOB} = \widehat {AOC} = 60^\circ ,\widehat {BOC} = 90^\circ \)
a. Chứng tỏ rằng ABC là tam giác vuông và OA ⊥ BC
b. Tìm đường vuông góc chung IJ của OA và BC ; tính khoảng cách giữa hai đường thẳng OA và BC.
c. Chứng minh rằng hai mặt phẳng (ABC) và (OBC) vuông góc với nhau.
Lời giải chi tiết
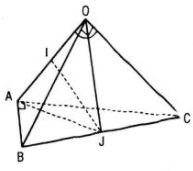
a. Vì \(\widehat {AOB} = \widehat {AOC} = 60^\circ \)
OA = OB = OC = a
Nên AB = AC = a
Suy ra ΔABC = ΔOBC
Vậy tam giác ABC vuông cân tại A
Gọi J là trung điểm của BC thì OJ ⊥ BC, AJ ⊥ BC nên OA ⊥ BC.
Cách khác:

b. Gọi I là trung điểm của OA, do OJ = AJ nên JI ⊥ OA, mà JI ⊥ BC, vậy IJ là đường vuông góc chung của OA và BC.
\(I{J^2} = O{J^2} - O{I^2} = {\left( {{{a\sqrt 2 } \over 2}} \right)^2} - {\left( {{a \over 2}} \right)^2} = {{{a^2}} \over 4}.\)
Suy ra : d(OA ; BC) = \({a \over 2}\)
c. Từ các kết quả trên ta có : OJ ⊥ BC, AJ ⊥ BC, IJ = \({1 \over 2}OA\)
Vậy góc giữa mp(OBC) và mp(ABC) bằng góc \(\widehat {OJA}\) và \(\widehat {OJA} = 90^\circ ,\) do đó mp(OBC) ⊥ mp(ABC).