Câu 17 trang 204 SGK Đại số và Giải tích 11 Nâng cao — Không quảng cáo

Tìm đạo hàm của mỗi hàm số sau (a và b là hằng số

LG a

\(y = {x^5} - 4{x^3} + 2x - 3\sqrt x \)

Phương pháp giải:

Sử dụng công thức

+) \(\left( {{x^n}} \right)' = n{x^{n - 1}}\)

+) \(\left( {\sqrt x } \right)' = \dfrac{1}{{2\sqrt x }}\)

và các công thức đạo hàm của tổng, hiệu, tích một hàm số với một số thực.

Lời giải chi tiết:

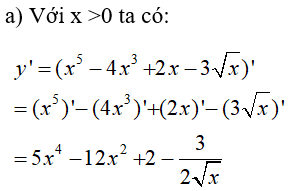
LG b

\(y = {1 \over 4} - {1 \over 3}x + {x^2} - 0,5{x^4}\)

Lời giải chi tiết:

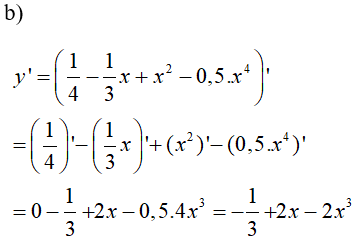
LG c

\(y = {{{x^4}} \over 4} - {{{x^3}} \over 3} + {{{x^2}} \over 2} - x + {a^3}\)

Lời giải chi tiết:

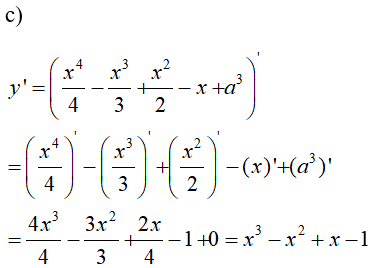
\(y' = {x^3} - {x^2} + x - 1\)

LG d

\(y = {{ax + b} \over {a + b}}\)

Lời giải chi tiết:

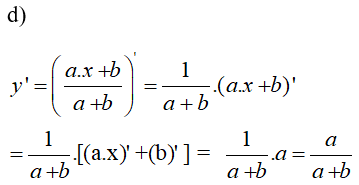
\(y = {a \over {a + b}}\)