Câu 19 trang 103 SGK Hình học 11 Nâng cao
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và SA = SB = SC = b. Gọi G là trọng tâm tam giác ABC.
Đề bài
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và SA = SB = SC = b. Gọi G là trọng tâm tam giác ABC.
a. Chứng minh rằng SG ⊥ (ABC). Tính SG.
b. Xét mặt phẳng (P) đi qua A và vuông góc với đường thẳng SC. Tìm hệ thức liên hệ giữa a và b để (P) cắt SC tại điểm C 1 nằm giữa S và C. Khi đó hãy tính diện tích thiết diện của hình chóp S.ABC khi cắt bởi mp(P).
Lời giải chi tiết
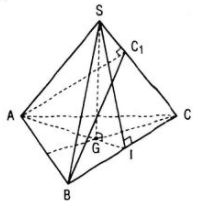
a. Gọi I là trung điểm của BC.
Tam giác ABC đều, AI là đường trung tuyến nên đồng thời là đường cao: BC ⊥ AI.
Tam giác SBC có SB = SC, SI là đường trung tuyến nên đồng thời là đường cao: BC ⊥ SI.
\(\begin{array}{l} \Rightarrow BC \bot (SAI) \supset SG\\ \Rightarrow BC \bot SG.\,\,\, (1) \end{array}\)
Chứng minh tương tự ta có: \(AB \bot SG\,\,\, (1)\)
Từ (1;2) suy ra \(SG \bot (ABC)\)
\(\begin{array}{l} +) \, SI^2 ={S{C^2} - I{C^2}} ={{b^2} - \frac{{{a^2}}}{4}} \\ +) \, GI = \frac{1}{3}AI;\, AI ^2 = {A{B^2} - B{I^2}} =a.\frac{{3 }}{4} \Rightarrow GI= \frac{{a\sqrt 3 }}{6}. \end{array}\)
\(\Rightarrow SG = \sqrt {S{I^2} - G{I^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{4} - {{{a^2}} \over {12}}} \) \( = \sqrt {{{12{b^2} - 4{a^2}} \over {12}}}\) \( = \sqrt {{{3{b^2} - {a^2}} \over 3}} \)
b. Kẻ AC 1 ⊥ SC thì (P) chính là mp(ABC 1 )
Vì SAC là tam giác cân mà AC 1 ⊥ SC nên C 1 nằm giữa S và C khi và chỉ khi
\(\widehat {ASC} < 90^\circ \Leftrightarrow A{S^2} + C{S^2} > A{C^2} \) \(\Leftrightarrow 2{b^2} > {a^2}\)
Ta có : AB ⊥ GC và AB ⊥ SG ⇒ AB ⊥ SC
SC ⊥ AC 1 và SC ⊥ AB nên SC ⊥ (ABC 1 )
Thể tích tứ diện SABC là :
\(\eqalign{ & {V_{SABC}} = {1 \over 3}SG.{S_{ABC}} = {1 \over 3}SC.{S_{AB{C_1}}} \cr & \Rightarrow {S_{AB{C_1}}} = {{SG.{S_{ABC}}} \over {SC}} \cr &= {{\sqrt {{{3{b^2} - {a^2}} \over 3}} .{{{a^2}\sqrt 3 } \over 4}} \over b} = {{{a^2}\sqrt {3{b^2} - {a^2}} } \over {4b}} \cr} \)