Câu 19 trang 204 SGK Đại số và Giải tích 11 Nâng cao
Tìm đạo hàm của mỗi hàm số sau
Tìm đạo hàm của mỗi hàm số sau
LG a
\(y = {\left( {x - {x^2}} \right)^{32}}\)
Phương pháp giải:
Công thức \(\left( {{u^n}} \right)' = n{u^{n - 1}}u'\)
Lời giải chi tiết:
y' = 32.(x- x 2 ) 31 .(x - x 2 )'
= 32(x - x 2 ) 31 .(1 - 2x)
Vậy \(y' = 32{\left( {x - {x^2}} \right)^{31}}\left( {1 - 2x} \right)\)
LG b
\(y = {1 \over {x\sqrt x }}\)
Phương pháp giải:
Sử dụng công thức \(\left( {\frac{1}{u}} \right)' = \frac{{ - u'}}{{{u^2}}}\)
Lời giải chi tiết:
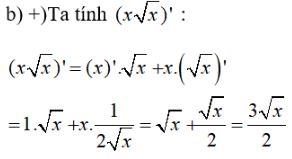
\( \Rightarrow \left( {\frac{1}{{x\sqrt x }}} \right)' = \frac{{ - \left( {x\sqrt x } \right)'}}{{{{\left( {x\sqrt x } \right)}^2}}} \) \(= \frac{{ - \frac{{3\sqrt x }}{2}}}{{{x^2}.x}} = - \frac{3}{{2{x^2}\sqrt x }}\)
\(y' = {{ - 3} \over {2{x^2}\sqrt x }}\)
LG c
\(y = {{1 + x} \over {\sqrt {1 - x} }}\)
Phương pháp giải:
Công thức đạo hàm của một thương: \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\)
Lời giải chi tiết:
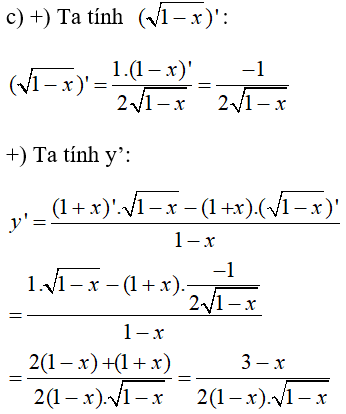
\(y' = {{3 - x} \over {2\sqrt {{{\left( {1 - x} \right)}^3}} }}\)
LG d
\(y = {x \over {\sqrt {{a^2} - {x^2}} }}\) (a là hằng số)
Phương pháp giải:
Công thức đạo hàm của một thương: \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\).
Lời giải chi tiết:
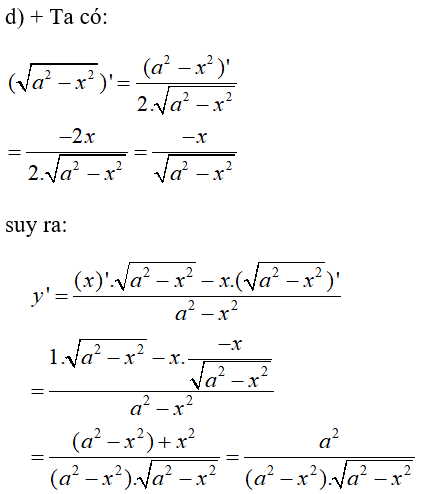
\(\eqalign{ & y' = {{{a^2}} \over {\sqrt {{{\left( {{a^2} - {x^2}} \right)}^3}} }} \cr} \)