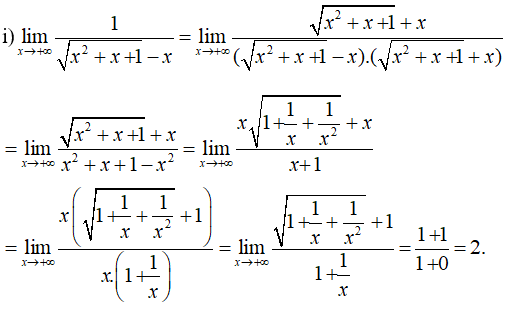Câu 19 trang 226 SGK Đại số và Giải tích 11 Nâng cao
Tính giới hạn của các hàm số sau :
Tính giới hạn của các hàm số sau :
LG a
lim
Lời giải chi tiết:
\mathop {\lim }\limits_{x \to - 1} {{{x^2} + x + 10} \over {{x^3} + 6}} = {{1 + \left( { - 1} \right) + 10} \over { - 1 + 6}} = 2
LG b
\mathop {\lim }\limits_{x \to - 5} {{{x^2} + 11x + 30} \over {25 - {x^2}}}
Lời giải chi tiết:
\mathop {\lim }\limits_{x \to - 5} {{{x^2} + 11x + 30} \over {25 - {x^2}}} = \mathop {\lim }\limits_{x \to - 5} {{\left( {x + 5} \right)\left( {x + 6} \right)} \over {\left( {5 - x} \right)\left( {5 + x} \right)}} = \mathop {\lim }\limits_{x \to - 5} {{x + 6} \over {5 - x}} = {1 \over {10}}
LG c
\mathop {\lim }\limits_{x \to - \infty } {{{x^6} + 4{x^2} + x - 2} \over {{{\left( {{x^3} + 2} \right)}^2}}}
Lời giải chi tiết:
\mathop {\lim }\limits_{x \to - \infty } {{{x^6} + 4{x^2} + x - 2} \over {{{\left( {{x^3} + 2} \right)}^2}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^6}\left( {1 + \frac{4}{{{x^4}}} + \frac{1}{{{x^5}}} - \frac{2}{{{x^6}}}} \right)}}{{{{\left[ {{x^3}\left( {1 + \frac{2}{{{x^3}}}} \right)} \right]}^2}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^6}\left( {1 + \frac{4}{{{x^4}}} + \frac{1}{{{x^5}}} - \frac{2}{{{x^6}}}} \right)}}{{{x^6}{{\left( {1 + \frac{2}{{{x^3}}}} \right)}^2}}} = \mathop {\lim }\limits_{x \to - \infty } {{1 + {4 \over {{x^4}}} + {1 \over {{x^5}}} - {2 \over {{x^6}}}} \over {{{\left( {1 + {2 \over {{x^3}}}} \right)}^2}}} = \frac{{1 + 0 + 0 - 0}}{{{{\left( {1 + 0} \right)}^2}}}= 1
LG d
\mathop {\lim }\limits_{x \to + \infty } {{{x^2} + x - 40} \over {2{x^5} + 7{x^4} + 21}}
Lời giải chi tiết:
\mathop {\lim }\limits_{x \to + \infty } {{{x^2} + x - 40} \over {2{x^5} + 7{x^4} + 21}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^5}\left( {\frac{1}{{{x^3}}} + \frac{1}{{{x^4}}} - \frac{{40}}{{{x^5}}}} \right)}}{{{x^5}\left( {2 + \frac{7}{x} + \frac{{21}}{{{x^5}}}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } {{{1 \over {{x^3}}} + {1 \over {{x^4}}} - {{40} \over {{x^5}}}} \over {2 + {7 \over x} + {{21} \over {{x^5}}}}} = \frac{{0 + 0 - 0}}{{2 + 0 + 0}} = 0
LG e
\mathop {\lim }\limits_{x \to - \infty } {{\sqrt {2{x^4} + 4{x^2} + 3} } \over {2x + 1}}
Lời giải chi tiết:
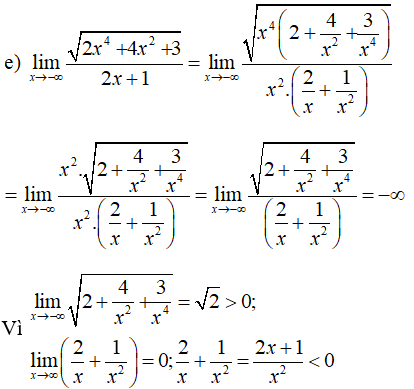
LG f
\mathop {\lim }\limits_{x \to + \infty } \left( {2x + 1} \right)\sqrt {{{x + 1} \over {2{x^3} + x}}}
Lời giải chi tiết:
LG g
\mathop {\lim }\limits_{x \to + \infty } \sqrt {9{x^2} + 11x - 100}
Lời giải chi tiết:
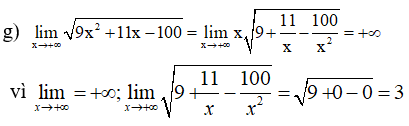
LG h
\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {5{x^2} + 1} - x\sqrt 5 } \right)
Lời giải chi tiết:
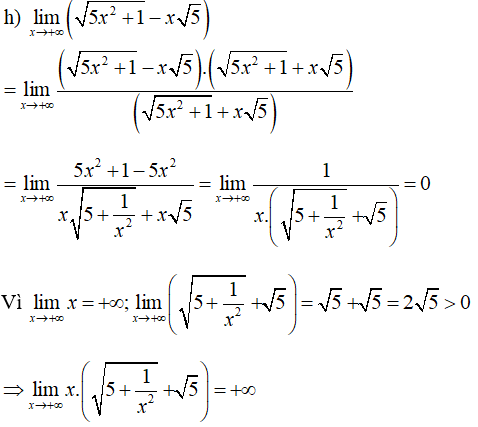
LG i
\mathop {\lim }\limits_{x \to + \infty } {1 \over {\sqrt {{x^2} + x + 1} - x}}
Lời giải chi tiết:
