Đề kiểm tra 15 phút - Đề số 2 - Bài 3 - Chương 3 - Hình học 9 — Không quảng cáo

Đề bài

Cho ∆ABC nội tiếp đường tròn (O). Tia phân giác của góc A cắt BC ở D và cắt đường tròn ở E. Chứng minh rằng:

a) $AB . AC = AD . AE$

b) $B{E^2} = AE.DE.$

Lời giải chi tiết

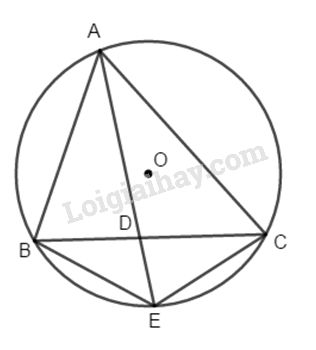
a) Ta có AE là phân giác của góc A nên:

$\widehat {BAE} = \widehat {CAE}$ $\Rightarrow$ cung BE = cung CE

Lạicó: $\widehat {ABC} = \widehat {AEC}$ ( góc nội tiếp cùng chắn cung AC)

Do đó ∆ABD đồng dạng với ∆AEC (g.g)

$\Rightarrow\dfrac{{AB} }{ {AE}} = \dfrac{{AD} }{{AC}}$ $\Rightarrow AB . AC = AD . AE$.

b) Xét ∆ABE và ∆BDE có :

+) $\widehat {AEB}$ chung

+) $\widehat {BAE} = \widehat {EBC}$ ( góc nội tiếp cùng chắn hai cung bằng nhau, cung BE = cung CE)

Do đó ∆ABE đồng dạng với ∆BDE (g.g)

$\Rightarrow \dfrac{{BE} }{ {DE}} = \dfrac{{AE} }{ {BE}} \Rightarrow B{E^2} = AE.DE$.