Đề kiểm tra 15 phút - Đề số 4 - Bài 3 - Chương 2 - Hình học 9 — Không quảng cáo

Đề bài

Bài 1. Cho điểm M nằm bên trong đường tròn (O; R). Dựng qua M hai dây AB và CD sao cho $AB > CD$. Gọi H, K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng : $MH > MK.$

Bài 2. Cho đường tròn (O) đường kính AB. Chứng minh rằng nếu hai dây cung AC và BD song song thì bằng nhau.

Lời giải chi tiết

Bài 1.

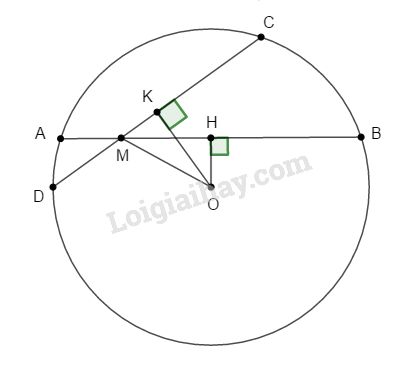
Nối M với O. Xét tam giác vuông OHM, ta có:

$HM = \sqrt {O{M^2} - O{H^2}}$$\;  = \sqrt {O{M^2} - O{H^2}}$ (định lí Pi-ta-go)

Tương tự với tam giác vuông OKM, có:

$KM = \sqrt {O{M^2} - O{K^2}}$

Mà $AB > CD ⇒ OH < OK$

Do đó $MH > MK$

Bài 2.

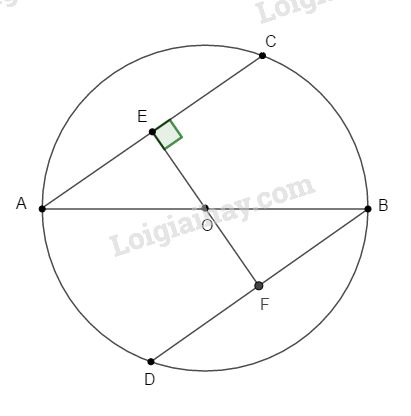
Kẻ $OE ⊥ AC$ thì đường thẳng $OE ⊥ BD$ và cắt BD tại F (vì AC // BD)

Xét hai tam giác vuông AEO và BOF có:

+) $OA = OB (=R)$

+) ${\widehat O_1} = {\widehat O_2}$ (đối đỉnh)

Do đó $∆AEO = ∆BOF$ (cạnh huyền – góc nhọn)

$⇒ OE = OF$ $⇒ AC = BD$ (định lí dây cung và khoảng cách đến tâm).