Đề kiểm tra giữa kì 1 Toán 9 - Đề số 12 có lời giải chi tiết — Không quảng cáo

Tải về đề thi và đáp án Tải về đề thi Tải về đáp án

Đề bài

Câu 1: Thực hiện phép tính:

a) $4\sqrt 5  - 3\sqrt {20}  + \sqrt {45}$

b) $\sqrt {{{(\sqrt 3  - 1)}^2}}  + \frac{6}{{\sqrt 3 }} - 15\sqrt {\frac{1}{3}}  + 1$

Câu 2: Giải phương trình:

a) $\sqrt {x - 3}  + \sqrt {9x - 27}  - \frac{1}{2}\sqrt {4x - 12}  = 6$

b) $\sqrt {{x^2} - 2x + 1}  + 2 = 5$

Câu 3: Cho hai biểu thức $A = \frac{{3\sqrt x }}{{\sqrt x {\rm{ \;}} + 2}}$ và $B = \frac{{x + 4}}{{x - 4}} - \frac{2}{{\sqrt x {\rm{ \;}} - 2}}$ với $x \ge 0,x \ne 4$.

1) Tính giá trị của biểu thức A khi x = 9.

2) Chứng minh $B = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} + 2}}$.

3) Tìm số nguyên dương x lớn nhất thỏa mãn $A - B < \frac{3}{2}$.

Câu 4 : Một tòa tháp có bóng trên mất đất dài 15m, biết rằng góc tạo bởi tia nằng mặt trời với mặt đất là ${55^0}$ (minh họa như hình vẽ bên dưới). Chiều cao của tòa tháp (làm tròn đến chữ số thập phân thức hai) bằng bao nhiêu?

Câu 5: Cho $\Delta EMF$ vuông tại M có đường cao MI. Vẽ $IP \bot ME{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {P \in ME} \right),$ $IQ \bot MF{\mkern 1mu} {\mkern 1mu} \left( {Q \in MF} \right).$

a) Cho biết $ME = 4{\mkern 1mu} cm,{\mkern 1mu} {\mkern 1mu} \sin \widehat {MFE} = \frac{3}{4}.$ Tính độ dài các đoạn $EF,{\mkern 1mu} {\mkern 1mu} EI,{\mkern 1mu} {\mkern 1mu} MI.$

b) Chứng minh $MP.PE + MQ.QF = M{I^2}.$

Câu 6: Cho 4 số thực dương a, b, c, d chứng mình rằng trong 4 số ${a^2} + \frac{1}{b} + \frac{1}{c};$ ${b^2} + \frac{1}{c} + \frac{1}{d};$${c^2} + \frac{1}{d} + \frac{1}{a};{d^2} + \frac{1}{a} + \frac{1}{b}$tồn tại ít nhất 1 số không nhỏ hơn 3.

-------- Hết --------

Lời giải chi tiết

Câu 1: Thực hiện phép tính:

a) $4\sqrt 5  - 3\sqrt {20}  + \sqrt {45}$

b) $\sqrt {{{(\sqrt 3  - 1)}^2}}  + \frac{6}{{\sqrt 3 }} - 15\sqrt {\frac{1}{3}}  + 1$

Phương pháp:

Công thức khai phương căn bậc hai, trục căn thức.

Cách giải:

a) $4\sqrt 5  - 3\sqrt {20}  + \sqrt {45}$

$\begin{array}{l} = 4\sqrt 5  - 3\sqrt {4.5}  + \sqrt {9.5} \\ = 4\sqrt 5  - 6\sqrt 5  + 3\sqrt 5 \\ = \sqrt 5 \end{array}$

b) $\sqrt {{{(\sqrt 3  - 1)}^2}}  + \frac{6}{{\sqrt 3 }} - 15\sqrt {\frac{1}{3}}  + 1$

$\begin{array}{l} = \left| {\sqrt 3  - 1} \right| + \frac{{6\sqrt 3 }}{3} - 15\sqrt {\frac{3}{9}}  + 1\\ = \sqrt 3  - 1 + 2\sqrt 3  - 5\sqrt 3  + 1\\ =  - 2\sqrt 3 \end{array}$

Câu 2: Giải phương trình:

a) $\sqrt {x - 3}  + \sqrt {9x - 27}  - \frac{1}{2}\sqrt {4x - 12}  = 6$

b) $\sqrt {{x^2} - 2x + 1}  + 2 = 5$

Phương pháp:

a) Tìm điều kiện xác định, đưa các hệ số ra ngoài căn và rút gọn

b) Dùng $\sqrt {{a^2}}  = \left| a \right|$ để bỏ căn bậc hai và giải phương trình chứa dấu giá trị tuyệt đối.

Cách giải:

a) $\sqrt {x - 3}  + \sqrt {9x - 27}  - \frac{1}{2}\sqrt {4x - 12}  = 6$

ĐKXĐ: $x \ge 3$

$\begin{array}{l}pt \Leftrightarrow \sqrt {x - 3}  + \sqrt {9\left( {x - 3} \right)}  - \frac{1}{2}\sqrt {4\left( {x - 3} \right)}  = 6\\ \Leftrightarrow \sqrt {x - 3}  + 3\sqrt {x - 3}  - \sqrt {x - 3}  = 6\\ \Leftrightarrow 3\sqrt {x - 3}  = 6\\ \Leftrightarrow \sqrt {x - 3}  = 2\\ \Leftrightarrow x - 3 = 4\\ \Leftrightarrow x = 7\left( {TM} \right)\\ \Rightarrow S = \left\{ 7 \right\}\end{array}$

b) $\sqrt {{x^2} - 2x + 1}  + 2 = 5$

Đk: với mọi giá trị của x

$\begin{array}{l}pt \Leftrightarrow \sqrt {{{\left( {x - 1} \right)}^2}}  + 2 = 5\\ \Leftrightarrow \left| {x - 1} \right| + 2 = 5\\ \Leftrightarrow \left| {x - 1} \right| = 3\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 3\\x - 1 =  - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 4\\x =  - 2\end{array} \right.\left( {tm} \right)\\ \Rightarrow S = \left\{ { - 2,4} \right\}\end{array}$

Câu 3: Cho hai biểu thức $A = \frac{{3\sqrt x }}{{\sqrt x {\rm{ \;}} + 2}}$ và $B = \frac{{x + 4}}{{x - 4}} - \frac{2}{{\sqrt x {\rm{ \;}} - 2}}$ với $x \ge 0,x \ne 4$.

1) Tính giá trị của biểu thức A khi x = 9.

2) Chứng minh $B = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} + 2}}$.

3) Tìm số nguyên dương x lớn nhất thỏa mãn $A - B < \frac{3}{2}$.

Phương pháp:

1) Kiểm tra giá trị của x có thỏa mãn điều kiện sau đó thay vào biểu thức và tính.

2) Vận dụng hằng đẳng thức $a - b = \left( {\sqrt a {\rm{\;}} - \sqrt b } \right)\left( {\sqrt a {\rm{\;}} + \sqrt b } \right)$ xác định mẫu thức chung của biểu thức

Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.

3) Tính hiệu $A - B$. Giải bất phương trình $A - B < \frac{3}{2}$

Cách giải:

1) Với x = 9 thỏa mãn điều kiện, thay vào A, ta được: $A = \frac{{3\sqrt 9 }}{{\sqrt 9 {\rm{\;}} + 2}} = \frac{{3.3}}{{3 + 2}} = \frac{9}{5}$

Vậy với x = 9 thì $A = \frac{9}{5}$.

2) Với $x \ge 0,x \ne 4$, ta có:

$B = \frac{{x + 4}}{{x - 4}} - \frac{2}{{\sqrt x {\rm{\;}} - 2}}$

3) Ta có $A - B = \frac{{3\sqrt x }}{{\sqrt x  + 2}} - \frac{{\sqrt x }}{{\sqrt x  + 2}}$

$\begin{array}{*{20}{l}}{ = \frac{{3\sqrt x {\rm{\;}} - \sqrt x }}{{\sqrt x {\rm{\;}} + 2}}}\\{ = \frac{{2\sqrt x }}{{\sqrt x {\rm{\;}} + 2}}}\end{array}$

Để $A - B < \frac{3}{2} \Leftrightarrow \frac{{2\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} < \frac{3}{2}$

$\begin{array}{*{20}{l}}{ \Leftrightarrow \frac{{2\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} - \frac{3}{2} < 0}\\{ \Leftrightarrow \frac{{2.2\sqrt x {\rm{\;}} - 3\left( {\sqrt x {\rm{\;}} + 2} \right)}}{{2\left( {\sqrt x {\rm{\;}} + 2} \right)}} < 0}\\{ \Leftrightarrow \frac{{4\sqrt x {\rm{\;}} - 3\sqrt x {\rm{\;}} - 6}}{{2\left( {\sqrt x {\rm{\;}} + 2} \right)}} < 0}\\{ \Leftrightarrow \frac{{\sqrt x {\rm{\;}} - 6}}{{2\left( {\sqrt x {\rm{\;}} + 2} \right)}} < 0}\end{array}$

Vì $x \ge 0,x \ne 4 \Rightarrow 2\left( {\sqrt x {\rm{\;}} + 2} \right) > 0$

Do đó, $\sqrt x {\rm{\;}} - 6 < 0 \Leftrightarrow \sqrt x {\rm{\;}} < 6 \Leftrightarrow x < 36$

Kết hợp điều kiện: $x \ge 0,x \ne 4$ $\Rightarrow 0 \le x < 36,{\mkern 1mu} {\mkern 1mu} x \ne 4$.

Mà x là số nguyên dương lớn nhất nên x = 35

Vậy $x = 35.$

Câu 4 : Một tòa tháp có bóng trên mất đất dài 15m, biết rằng góc tạo bởi tia nằng mặt trời với mặt đất là ${55^0}$ (minh họa như hình vẽ bên dưới). Chiều cao của tòa tháp (làm tròn đến chữ số thập phân thức hai) bằng bao nhiêu?

Phương pháp:

Vận dụng tỉ số lượng giác của góc nhọn trong tam giác vuông.

Cách giải:

Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có: $= 15.\tan {55^0} \approx 21,42m$

Câu 5: Cho $\Delta EMF$ vuông tại M có đường cao MI. Vẽ $IP \bot ME{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {P \in ME} \right),$ $IQ \bot MF{\mkern 1mu} {\mkern 1mu} \left( {Q \in MF} \right).$

a) Cho biết $ME = 4{\mkern 1mu} cm,{\mkern 1mu} {\mkern 1mu} \sin \widehat {MFE} = \frac{3}{4}.$ Tính độ dài các đoạn $EF,{\mkern 1mu} {\mkern 1mu} EI,{\mkern 1mu} {\mkern 1mu} MI.$

b) Chứng minh $MP.PE + MQ.QF = M{I^2}.$

Phương pháp:

a) Sử dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông để tính độ dài các cạnh $EF,{\mkern 1mu} {\mkern 1mu} EI,{\mkern 1mu} {\mkern 1mu} MI.$

b) Sử dụng hệ thức lượng trong tam giác vuông để chứng minh đẳng thức.

Cách giải:

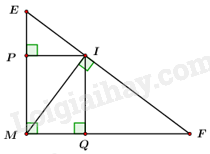
a) Cho biết $ME = 4{\mkern 1mu} cm,{\mkern 1mu} {\mkern 1mu} \sin \widehat {MFE} = \frac{3}{4}.$ Tính độ dài các đoạn $EF,{\mkern 1mu} {\mkern 1mu} EI,{\mkern 1mu} {\mkern 1mu} MI.$

Xét $\Delta MEF$ vuông tại$M$ ta có: $EF = \frac{{ME}}{{\sin \widehat {MFE}}} = \frac{4}{{\frac{3}{4}}} = \frac{{16}}{3}{\mkern 1mu} {\mkern 1mu} cm.$

$\Rightarrow MF = \sqrt {E{F^2} - M{E^2}} {\rm{\;}} = \sqrt {{{\left( {\frac{{16}}{3}} \right)}^2} - {4^2}}$ $= \sqrt {\frac{{112}}{9}} {\rm{\;}} = \frac{{4\sqrt 7 }}{3}{\mkern 1mu} {\mkern 1mu} cm.$

Xét $\Delta MIF$ vuông tại $I$ ta có: $MI = MF.\sin \widehat {MFE} = \frac{{4\sqrt 7 }}{3}.\frac{3}{4} = \sqrt 7 {\mkern 1mu} {\mkern 1mu} cm.$

Áp dụng định lý Pitago trong $\Delta MIE$ vuông tại $I$ ta có:

$EI = \sqrt {M{E^2} - M{I^2}}$ $= \sqrt {{4^2} - {{\left( {\sqrt 7 } \right)}^2}} {\rm{\;}} = \sqrt 9 {\rm{\;}} = 3{\mkern 1mu} {\mkern 1mu} cm.$

Vậy $EF = \frac{{16}}{3}{\mkern 1mu} {\mkern 1mu} cm,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} EI = 3{\mkern 1mu} {\mkern 1mu} cm,{\mkern 1mu} {\mkern 1mu} MI = \sqrt 7 {\mkern 1mu} {\mkern 1mu} cm.$

b) Chứng minh $MP.PE + MQ.QF = M{I^2}.$

Theo đề bài ta có: $\left\{ {\begin{array}{*{20}{l}}{IP \bot ME{\mkern 1mu}  = \left\{ P \right\}}\\{IQ \bot MF{\mkern 1mu}  = \left\{ Q \right\}}\end{array}} \right.$

Xét tứ giác MPIQ ta có: $\widehat {IPM} = \widehat {PMQ} = \widehat {MQI} = {90^0}$

$\Rightarrow MPIQ$ là hình chữ nhật (dhnb).

$\Rightarrow \left\{ {\begin{array}{*{20}{l}}{MP = IQ}\\{PI = MQ}\end{array}} \right.$ (tính chất hình chữ nhật).

Áp dụng hệ thức lượng trong $\Delta MEI$ vuông tại $I$ có đường cao IP ta có: $I{P^2} = MP.PE$

Áp dụng hệ thức lượng trong $\Delta MFI$ vuông tại $I$ có đường cao IQ ta có: $I{Q^2} = MQ.QF.$

$\Rightarrow M{P^2} = I{Q^2} = MQ.QF$

Áp dụng hệ thức lượng trong $\Delta MPI$ ta có:

$M{I^2} = M{P^2} + P{I^2}$ $= MP.PE + MQ.QF{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {dpcm} \right).$

Câu 6: Cho 4 số thực dương a, b, c, d chứng mình rằng trong 4 số ${a^2} + \frac{1}{b} + \frac{1}{c};$ ${b^2} + \frac{1}{c} + \frac{1}{d};$${c^2} + \frac{1}{d} + \frac{1}{a};{d^2} + \frac{1}{a} + \frac{1}{b}$tồn tại ít nhất 1 số không nhỏ hơn 3.

Phương pháp:

Chứng minh bằng phản chứng

Cách giải:

Giả sử bốn số ${a^2} + \frac{1}{b} + \frac{1}{c};{b^2} + \frac{1}{c} + \frac{1}{d};{c^2} + \frac{1}{d} + \frac{1}{a};{d^2} + \frac{1}{a} + \frac{1}{b}$ đều nhỏ hơn 3

Suy ra ${a^2} + \frac{1}{b} + \frac{1}{c} + {b^2} + \frac{1}{c} + \frac{1}{d} + {c^2} + \frac{1}{d} + \frac{1}{a} + {d^2} + \frac{1}{a} + \frac{1}{b} < 12$   (1)

Ta lại có

$\begin{array}{*{20}{l}}{{a^2} + \frac{1}{b} + \frac{1}{c} + {b^2} + \frac{1}{c} + \frac{1}{d} + {c^2} + \frac{1}{d} + \frac{1}{a} + {d^2} + \frac{1}{a} + \frac{1}{b} = {a^2} + {b^2} + {c^2} + {d^2} + \frac{2}{a} + \frac{2}{b} + \frac{2}{c} + \frac{2}{d}}\\{{a^2} + \frac{1}{a} + \frac{1}{a} \ge 3\sqrt[3]{{{a^2}.\frac{1}{a}.\frac{1}{a}}} = 3{\mkern 1mu} {\mkern 1mu} \left( {BDT{\mkern 1mu} {\mkern 1mu} Co - si} \right)}\end{array}$

Tương tự với b; c; d

Suy ra ${a^2} + {b^2} + {c^2} + {d^2} + \frac{2}{a} + \frac{2}{b} + \frac{2}{c} + \frac{2}{d} \ge 3.4 = 12{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right)$

Từ (1) và  (2) suy ra vô lý

Vậy tồn tại ít nhất 1 số không nhỏ hơn 3 (đpcm).