Đề kiểm tra giữa kì 1 Toán 9 - Đề số 9 có lời giải chi tiết — Không quảng cáo

Tải về đề thi và đáp án Tải về đề thi Tải về đáp án

Đề bài

Bài 1 ( 2,5 điểm)

Cho hai biểu thức $A = \frac{{\sqrt x + 1}}{{\sqrt x - 3}}$ và $B = \frac{{x - 3}}{{x - 9}} + \frac{1}{{\sqrt x + 3}} - \frac{2}{{3 - \sqrt x }}$ với $x \ge 0$ ; $x \ne 9$ .

a) Tính giá trị của biểu thức $A$ với $x = 0,25$ .

b) Rút gọn biểu thức $B$ .

c) Cho $P = \frac{B}{A}$ . Chứng minh rằng $P < 1$ với mọi giá trị $x$ thỏa mãn điều kiện.

Bài 2 (2,0 điểm) Tìm $x$ , biết

a) $\sqrt {25x + 75} + 15.\sqrt {\frac{{x + 3}}{{25}}} = 2 + 4\sqrt {x + 3}$

b) $\sqrt {{x^2} - 2x + 1} = 2x + 3$

Bài 3 (1,5 điểm)

Một chiếc thang dài $3,5$ m. Cần đặt chân thang cách tường một khoảng bằng bao nhiêu để nó tạo với phương nằm ngang của mặt đất một góc an toàn $65^\circ$ . (làm tròn kết quả đến chữ số thập phân thứ hai)

Bài 4 (3,5 điểm)

Cho đường tròn $(O;R)$ , đường kính $AB$ . Kẻ tiếp tuyến $Ax$ , lấy điểm $C$ trên $Ax(AC > R)$ . Từ $C$ kẻ tiếp tuyến tại $CD$ với $(O)$ $(D$ là tiếp điểm $)$ .

a) Chứng minh bốn điểm $A\,,C,D,O$ cùng thuộc một đường tròn.

b) Chứng minh $OC{\mkern 1mu} {\rm{//}}{\mkern 1mu} BD$ .

c) Đường thẳng vuông góc với $A\,B$ tại $O$ cắt tia $BD$ tại $M$ . Chứng minh $OMCD$ là hình bình hành.

d) Gọi $K$ là giao điểm của $CD$ và $OM$ , $E$ là giao điểm của $CD$ và $OD$ ; $I$ là giao điểm của $AM$ và $OC$ . Chứng minh $E$ , $K$ , $I$ thẳng hàng.

Bài 5 (0,5 điểm) Cho $x$ , $y$ , $z$ là các số thực không âm thỏa mãn $x + y + z = 1$ . Tính giá trị biểu thức $P = \sqrt {2{x^2} + x + 1} + \sqrt {2{y^2} + y + 1} + \sqrt {2{z^2} + z + 1}$

-------- Hết --------

Lời giải chi tiết

Bài 1 ( 2,5 điểm)

Cho hai biểu thức $A = \frac{{\sqrt x + 1}}{{\sqrt x - 3}}$ và $B = \frac{{x - 3}}{{x - 9}} + \frac{1}{{\sqrt x + 3}} - \frac{2}{{3 - \sqrt x }}$ với $x \ge 0$ ; $x \ne 9$ .

a) Tính giá trị của biểu thức $A$ với $x = 0,25$ .

b) Rút gọn biểu thức $B$ .

c) Cho $P = \frac{B}{A}$ . Chứng minh rằng $P < 1$ với mọi giá trị $x$ thỏa mãn điều kiện.

Phương pháp

a) Kiểm tra $x = 0,25$ có thỏa mãn điều kiện hay không, sau đó thay vào biểu thức A để tính.

b) Xác định mẫu thức chung, quy đồng và thực hiện các phép toán với các phân thức đại số.

c) Tính $P = \frac{B}{A}$ . Chứng minh P – 1 < 0.

Lời giải

a) Tính giá trị của biểu thức $A$ với $x = 0,25$ .

Thay $x = 0,25$ (tmdk) vào biểu thức $A$ ta được:

$A = \frac{{\sqrt x + 1}}{{\sqrt x - 3}} = \frac{{\sqrt {0,25} + 1}}{{\sqrt {0,25} - 3}} = \frac{{0,5 + 1}}{{0,5 - 3}} = \frac{{1,5}}{{ - 2,5}} = - \frac{3}{5}$

b) Rút gọn biểu thức $B$ .

$B = \frac{{x - 3}}{{x - 9}} + \frac{1}{{\sqrt x + 3}} - \frac{2}{{3 - \sqrt x }}$ với $x \ge 0$ ; $x \ne 9$ .

$\begin{array}{l}B = \frac{{x - 3}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}} + \frac{1}{{\sqrt x + 3}} + \frac{2}{{\sqrt x - 3}}\\B = \frac{{x - 3 + \sqrt x - 3 + 2\left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}} = \frac{{x + 3\sqrt x }}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}} = \frac{{\sqrt x \left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}\end{array}$

$B = \frac{{\sqrt x }}{{\sqrt x - 3}}$ .

c) Cho $P = \frac{B}{A}$ . Chứng minh rằng $P < 1$ với mọi giá trị $x$ thỏa mãn điều kiện: $x \ge 0$ ; $x \ne 9$ .

$P = \frac{B}{A} = \frac{{\sqrt x }}{{\sqrt x - 3}}:\frac{{\sqrt x + 1}}{{\sqrt x - 3}} = \frac{{\sqrt x \left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 1} \right)}} = \frac{{\sqrt x }}{{\sqrt x + 1}}$

Xét $P - 1 = \frac{{\sqrt x }}{{\sqrt x + 1}} - 1 = \frac{{ - 1}}{{\sqrt x + 1}}$

Vì $\sqrt x + 1 > 0$ ; $- 1 < 0$ nên $\frac{{ - 1}}{{\sqrt x + 1}} < 0$ với $x \ge 0$ ; $x \ne 9$ .

$\Rightarrow P - 1 < 0$ với $x \ge 0$ ; $x \ne 9$ .

Bài 2 (2,0 điểm) Tìm $x$ , biết

a) $\sqrt {25x + 75} + 15.\sqrt {\frac{{x + 3}}{{25}}} = 2 + 4\sqrt {x + 3}$

b) $\sqrt {{x^2} - 2x + 1} = 2x + 3$

Phương pháp

Xác định điều kiện xác định của phương trình.

a) Đưa các hệ số ra ngoài căn, nhóm nhân tử chung để tìm x.

b) Sử dụng hằng đẳng thức để biến đổi vế trái về trị tuyệt đối để tìm x.

Lời giải

a) $\sqrt {25x + 75} + 15.\sqrt {\frac{{x + 3}}{{25}}} = 2 + 4\sqrt {x + 3}$

$\Leftrightarrow 5\sqrt {x + 3} + 3.\sqrt {x + 3} = 2 + 4\sqrt {x + 3}$

$\Leftrightarrow 5\sqrt {x + 3} + 3.\sqrt {x + 3} - 4\sqrt {x + 3} = 2$

$\Leftrightarrow 4\sqrt {x + 3} = 2$ (đk: $x \ge - 3$ )

$\Leftrightarrow \sqrt {x + 3} = \frac{1}{2}$

$\Leftrightarrow x + 3 = \frac{1}{4}$

$\Leftrightarrow x = \frac{{ - 11}}{4}$ (thỏa mãn)

Vậy phương trình có nghiệm $x = \frac{{ - 11}}{4}$

b) $\sqrt {{x^2} - 2x + 1} = 2x + 3$ (đk: $x \ge - \frac{3}{2}$ )

$\Leftrightarrow \sqrt {{{\left( {x - 1} \right)}^2}} = 2x + 3$

$\Leftrightarrow \left| {x - 1} \right| = 2x + 3$

$\Leftrightarrow \left[ \begin{array}{l}x - 1 = 2x + 3\\x - 1 = - 2x - 3\end{array} \right.$

$\Leftrightarrow \left[ \begin{array}{l}x - 1 = 2x + 3\\x - 1 = - 2x - 3\end{array} \right.$

$\Leftrightarrow \left[ \begin{array}{l}x = - 4\\3x = 2\end{array} \right.$

$\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 4}&{(L)}\\{x = \frac{2}{3}}&{(TM)}\end{array}} \right.$

Vậy phương trình có nghiệm $x = \frac{2}{3}$

Bài 3 (1,5 điểm)

Một chiếc thang dài $3,5$ m. Cần đặt chân thang cách tường một khoảng bằng bao nhiêu để nó tạo với phương nằm ngang của mặt đất một góc an toàn $65^\circ$ . (làm tròn kết quả đến chữ số thập phân thứ hai)

Phương pháp

Sử dụng hệ thức lượng trong tam giác vuông để tính.

Lời giải

Theo đề bài ta có hình vẽ sau

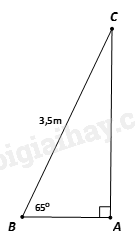
Ta có $BC = 3,5$ m; $\widehat {ABC} = 65^\circ$

Xét $\Delta ABC$ vuông tại $A$ , có:

$\cos \widehat {ABC} = \frac{{AB}}{{BC}}$ (hệ thức lượng trong tam giác vuông)

$\Rightarrow \cos 65^\circ = \frac{{AB}}{{3,5}}$

$\Rightarrow AB = 3,5.\cos 65^\circ$

$\Rightarrow AB \approx 1,48$ m

Vậy cần đặt thang sao cho chân thang cách tường khoảng $1,48$ m

Bài 4 (3,5 điểm)

Cho đường tròn $(O;R)$ , đường kính $AB$ . Kẻ tiếp tuyến $Ax$ , lấy điểm $C$ trên $Ax(AC > R)$ . Từ $C$ kẻ tiếp tuyến tại $CD$ với $(O)$ $(D$ là tiếp điểm $)$ .

a) Chứng minh bốn điểm $A\,,C,D,O$ cùng thuộc một đường tròn.

b) Chứng minh $OC{\mkern 1mu} {\rm{//}}{\mkern 1mu} BD$ .

c) Đường thẳng vuông góc với $A\,B$ tại $O$ cắt tia $BD$ tại $M$ . Chứng minh $OMCD$ là hình bình hành.

d) Gọi $K$ là giao điểm của $CD$ và $OM$ , $E$ là giao điểm của $CD$ và $OD$ ; $I$ là giao điểm của $AM$ và $OC$ . Chứng minh $E$ , $K$ , $I$ thẳng hàng.

Phương pháp

a) Chứng minh tam giác AOC và DOC thuộc đường tròn đường kính OC.

b) Chứng minh $OC\, \bot \,AD$ và $BD\, \bot \,AD$ nên OC // BD.

c) Chứng minh OMCD có cặp cạnh đối song song và bằng nhau.

d) Chứng minh KE vuông góc với CO tại I.

Lời giải

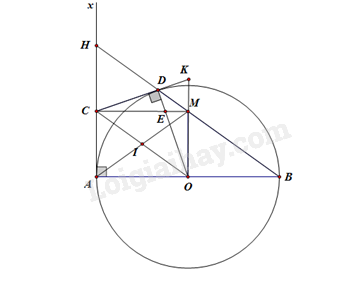
a) Chứng minh tam giác $AOC$ vuông tại $A$ nên $A$ thuộc đường tròn đường kính $OC$

Chứng minh tam giác $DOC$ vuông tại $D$ nên $D$ thuộc đường tròn đường kính $OC$

Do đó bốn điểm $A$ , $C$ , $D$ , $O$ cùng thuộc một đường tròn đường kính $OC$ .

b) Xét $\left( O \right)$ có: $CA$ , $CD$ là 2 tiếp tuyến cắt nhau tại $C$ ( gt)

Suy ra: $CA\, = \,CD$ (tính chất 2 tiếp tuyến cắt nhau)

Suy ra: $C$ thuộc trung trực của $AD$ (1)

Lại có: $OA = OD = R$

Suy ra $O$ thuộc đường tròn đường kính $AD$ (2)

Từ (1) và (2) suy ra: $OC$ là đường trung trực của $AD$

Suy ra: $OC\, \bot \,AD$

Ta lại chứng minh được : $BD\, \bot \,AD$

$\Rightarrow OC{\mkern 1mu} {\rm{//}}{\mkern 1mu} BD$

c) Kéo dài $BD$ cắt $AC$ tại $H$

Do $\left. \begin{array}{l}OA = OB\\CO{\mkern 1mu} {\rm{//}}{\mkern 1mu} BD\end{array} \right\} \Rightarrow CA = CH$

CM tương tự $M$ là trung điểm của $HB$

Xét tam giác $AHB$ có

$\left. \begin{array}{l}OA = OB\\CA = CH\end{array} \right\} \Rightarrow CO = \frac{1}{2}HB$

$\Rightarrow MB = CO$

Mà $MB{\mkern 1mu} {\rm{//}}{\mkern 1mu} CO$

Suy ra $OMCD$ là hình bình hành.

d) Chứng minh $AOMC$ là hình chữ nhật

$\Delta KMC = \Delta KDO \Rightarrow KC = KO \Rightarrow \Delta KOC$ cân tại $K$

Mà $\left. \begin{array}{l}OD \bot OB\\CM \bot KO\\CM \cap DO \equiv E\end{array} \right\} \Rightarrow EK \bot CO$

$\Delta KOC$ cân tại $K;IC = IO;EK \bot CO$ nên $E$ , $K$ , $I$ thẳng hàng.

Bài 5 (0,5 điểm) Cho $x$ , $y$ , $z$ là các số thực không âm thỏa mãn $x + y + z = 1$ . Tính giá trị biểu thức $P = \sqrt {2{x^2} + x + 1} + \sqrt {2{y^2} + y + 1} + \sqrt {2{z^2} + z + 1}$

Phương pháp

Dựa vào giả thiết suy ra với $0 \le a \le 1$ thì $2{a^2} + a + 1 \le {(a + 1)^2}$ để tính giá trị biểu thức P.

Lời giải

Do $x + y + z \le 1$ và $x,y,z$ là các số thực không âm

$\Rightarrow 0 \le x \le 1 \Rightarrow {x^2} \le x \Rightarrow {x^2} + {x^2} + x + 1 \le {x^2} + x + x + 1 \Rightarrow 2{x^2} + x + 1 \le {(x + 1)^2}$

Tương tự: $\Rightarrow 0 \le y \le 1 \Rightarrow 2{y^2} + y + 1 \le {(y + 1)^2}$

$\Rightarrow 0 \le z \le 1 \Rightarrow 2{z^2} + z + 1 \le {(z + 1)^2}$

Nên $P = \sqrt {2{x^2} + x + 1} + \sqrt {2{y^2} + y + 1} + \sqrt {2{z^2} + z + 1} \le x + 1 + y + 1 + z + 1$

$P \le (x + y + z) + 3 = 4 \Rightarrow {P_{max}} = 4$

Dấu “=” xảy ra $\Leftrightarrow x = y = 0;z = 1$ hoặc $\Leftrightarrow x = z = 0;y = 1$ hoặc $\Leftrightarrow y = z = 0;x = 1$