Đề kiểm tra giữa học kì 1 Toán 9 - Đề số 3
Đề bài
Cho tam giác $MNP$ vuông tại $M$. Khi đó $\cos \widehat {MNP}$ bằng
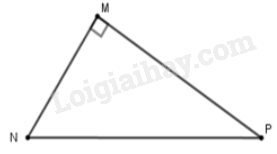
-
A.
$\dfrac{{MN}}{{NP}}$
-
B.
$\dfrac{{MP}}{{NP}}$
-
C.
$\dfrac{{MN}}{{MP}}$
-
D.
$\dfrac{{MP}}{{MN}}$
Cho tam giác $ABC$ vuông tại $A$ có $AB = 3cm,{\rm{ }}BC = 5cm.{\rm{ }}AH$ là đường cao. Tính $BH,CH,AC$ và $AH.$
-
A.
\(BH = 2\,cm\) , \(CH = 3,2\,cm\) , \(AC = 4\,cm\), \(AH = 2,4\,cm\)
-
B.
\(BH = 1,8\,cm\), \(CH = 3,2\,cm\), \(AC = 4\,cm\), \(AH = 2,4\,cm\).
-
C.
\(BH = 1,8\,cm\), \(CH = 3,2\,cm\), \(AC = 3\,cm\), \(AH = 2,4\,cm\)
-
D.
\(BH = 1,8\,cm\), \(CH = 3,2\,cm\), \(AC = 4\,cm\), \(AH = 4,2\,cm\)
Tính \(x\) trong hình vẽ sau:
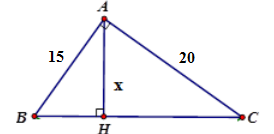
-
A.
\(x = 14\)
-
B.
\(x = 13\)
-
C.
\(x = 12\)
-
D.
\(x = \sqrt {145} \)
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) (như hình vẽ). Hệ thức nào sau đây là sai ?
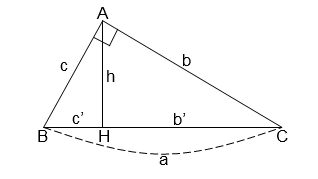
-
A.
\({b^2} = b'.a\)
-
B.
\(\dfrac{1}{{{h^2}}} = \dfrac{1}{{{c^2}}} + \dfrac{1}{{{b^2}}}\)
-
C.
\(a.h = b'.c'\)
-
D.
\({h^2} = b'.c'\)
Cho tam giác \(ABC\) vuông tại \(A,\) chiều cao \(AH\). Chọn câu sai.
-
A.
\(A{H^2} = BH.CH\)
-
B.
\(A{B^2} = BH.BC\)
-
C.
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)
-
D.
\(AH.AB = BC.AC\)
Khẳng định nào sau đây là sai ?
-
A.
\(a > b \Leftrightarrow \sqrt[3]{a} > \sqrt[3]{b}\)
-
B.
\(a < b \Leftrightarrow \sqrt[3]{a} < \sqrt[3]{b}\)
-
C.
\(a \ge b \Leftrightarrow \sqrt[3]{a} \ge \sqrt[3]{b}\)
-
D.
\(a < b \Leftrightarrow \sqrt[3]{a} > \sqrt[3]{b}\)
Khẳng định nào sau đây là đúng ?
-
A.
\(\sqrt {2018 + 2019} = \sqrt {2018} + \sqrt {2019} \)
-
B.
\(\sqrt {2018. 2019} = \dfrac{{\sqrt {2018} }}{{\sqrt {2019} }}\)
-
C.
\(\sqrt {2018} .\sqrt {2019} = \sqrt {2018.2019} \)
-
D.
\(2018. 2019 = \dfrac{{\sqrt {2019} }}{{\sqrt {2018} }}\)
Giá trị của biểu thức \(\sqrt {32} + \sqrt {50} - 3\sqrt 8 - \sqrt {18} \) là
-
A.
$1$
-
B.
$0$
-
C.
$2$
-
D.
$3$
Tìm điều kiện xác định của\(\sqrt {125 - 5x} \).
-
A.
\(x \le 15\)
-
B.
\(x \ge 25\)
-
C.
\(x \le 25\)
-
D.
\(x \ge 0\)
Đưa thừa số $\sqrt {81{{\left( {2 - y} \right)}^4}} $ ra ngoài dấu căn ta được ?
-
A.
$9\left( {2 - y} \right)$
-
B.
$81{\left( {2 - y} \right)^2}$
-
C.
$9{\left( {2 - y} \right)^2}$
-
D.
$ - 9{\left( {2 - y} \right)^2}$
Cạnh bên của tam giác \(ABC\) cân tại \(A\) dài $20cm$ , góc ở đáy là \(50^\circ \) Độ dài cạnh đáy của tam giác cân là (Kết quả làm tròn đến chữ số thập phân thứ nhất).
-
A.
\(25\,cm\)
-
B.
\(25,7\,cm\)
-
C.
\(26\,cm\)
-
D.
\(12,9\,cm\)
Một cầu trượt trong công viên có độ dốc là ${28^0}$ và có độ cao là $2,1m.$Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ hai).
-
A.
$3,95\,m$
-
B.
$3,8\,m$
-
C.
$4,5\,m$
-
D.
$4,47\,m$
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 10\,cm,\widehat C = 30^\circ .\) Tính $AB;BC$
-
A.
$AB = \dfrac{{5\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$
-
B.
$AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{14\sqrt 3 }}{3}$
-
C.
$AB = \dfrac{{10\sqrt 3 }}{3};BC = 20\sqrt 3 $
-
D.
$AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$
Một cột đèn có bóng trên mặt đất dài \(6m.\) Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng \({38^0}.\) Tính chiều cao của cột đèn. (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(4,6\,m\)
-
B.
\(4,69\,m\)
-
C.
\(5,7\,m\)
-
D.
\(6,49\,m\)
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là đúng ?
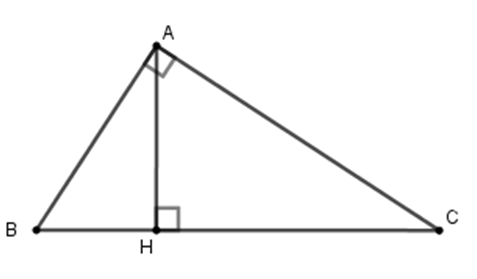
-
A.
$A{H^2} = AB.AC$
-
B.
$A{H^2} = BH.CH$
-
C.
$A{H^2} = AB.BH$
-
D.
$A{H^2} = CH.BC$
Chọn đáp án đúng.
-
A.
\(\dfrac{4}{{\sqrt 3 + 1}} + \dfrac{1}{{\sqrt 3 - 2}} + \dfrac{6}{{\sqrt 3 - 3}} = - 7 - \sqrt 3 \)
-
B.
\(\dfrac{4}{{\sqrt 3 + 1}} + \dfrac{1}{{\sqrt 3 - 2}} + \dfrac{6}{{\sqrt 3 - 3}} = 7\)
-
C.
\(\dfrac{4}{{\sqrt 3 + 1}} + \dfrac{1}{{\sqrt 3 - 2}} + \dfrac{6}{{\sqrt 3 - 3}} = - 7\)
-
D.
\(\dfrac{4}{{\sqrt 3 + 1}} + \dfrac{1}{{\sqrt 3 - 2}} + \dfrac{6}{{\sqrt 3 - 3}} = 7 + 7\sqrt 3 \)
Khẳng định nào sau đây là đúng?
-
A.
$\sqrt {{A^2}} = A\,\,\,khi\,\,A < 0$
-
B.
$\sqrt {{A^2}} = - A\,\,\,khi\,\,A \ge 0$
-
C.
$\sqrt A < \sqrt B \,\,\, \Leftrightarrow \,\,0 \le A < B$
-
D.
$A > B \Leftrightarrow \sqrt A < \sqrt B $
Cho tam giác $MNP$ vuông tại $N$. Hệ thức nào sau đây là đúng ?
-
A.
$MN = MP.\sin P$
-
B.
$MN = MP.\cos P$
-
C.
$MN = MP.\tan P$
-
D.
$MN = MP.\cot P$
Tìm giá trị của \(x\) không âm biết \(5\sqrt {2x} - 125 = 0\).
-
A.
\(x = \dfrac{{25}}{2}\)
-
B.
\(x = 125\)
-
C.
\(x = 25\)
-
D.
\(x = \dfrac{{625}}{2}\)
Rút gọn biểu thức \(\dfrac{{{a^2}}}{{11}}.\sqrt {\dfrac{{121}}{{{a^4}{b^{10}}}}} \) với \(ab \ne 0\) ta được:
-
A.
\(\dfrac{1}{{\left| {{b^5}} \right|}}\)
-
B.
\(\dfrac{1}{{{b^5}}}\)
-
C.
\({b^5}\)
-
D.
\(\dfrac{{11}}{{{b^5}}}\)
Trục căn thức ở mẫu biểu thức \(\dfrac{4}{{3\sqrt x + 2\sqrt y }}\) với \(x \ge 0;y \ge 0;x \ne \dfrac{4}{9}y\) ta được:
-
A.
\(\dfrac{{3\sqrt x - 2\sqrt y }}{{9x - 4y}}\)
-
B.
\(\dfrac{{12\sqrt x - 8\sqrt y }}{{3x + 2y}}\)
-
C.
\(\dfrac{{12\sqrt x + 8\sqrt y }}{{9x + 4y}}\)
-
D.
\(\dfrac{{12\sqrt x - 8\sqrt y }}{{9x - 4y}}\)
Rút gọn biểu thức \(2\sqrt {8\sqrt 3 } - 2\sqrt {5\sqrt 3 } - 3\sqrt {20\sqrt 3 } \)
-
A.
\(0\)
-
B.
\(4\sqrt {2\sqrt 3 } - 8\sqrt {5\sqrt 3 } \)
-
C.
\(\dfrac{3}{2}\sqrt 5 \)
-
D.
\(1\)
Rút gọn biểu thức \(3\sqrt {8a} + \dfrac{1}{4}\sqrt {\dfrac{{32a}}{{25}}} - \dfrac{a}{{\sqrt 3 }}.\sqrt {\dfrac{3}{{2a}}} - \sqrt {2a} \) với \(a > 0\) ta được:
-
A.
\(\dfrac{{47}}{{10}}\sqrt a \)
-
B.
\(\dfrac{{21}}{5}\sqrt a \)
-
C.
\(\dfrac{{47}}{{10}}\sqrt {2a} \)
-
D.
\(\dfrac{{47}}{5}\sqrt {2a} \)
Cho biểu thức \(A = \dfrac{{\sqrt x + 1}}{{\sqrt x - 2}}\) với \(x \ge 0;x \ne 4\). Tìm các giá trị của \(x\) biết \(A = \dfrac{{\sqrt x - 1}}{2}\) .
-
A.
\(x = 0;x = 5\)
-
B.
\(x = 0\)
-
C.
\(x = 0;x = 25\)
-
D.
\(x = 5;x = 1\)
Kết luận nào đúng khi nói về nghiệm của phương trình $\sqrt[3]{{3x - 2}} = - 2$
-
A.
Là số nguyên âm
-
B.
Là phân số
-
C.
Là số vô tỉ
-
D.
Là số nguyên dương
Thu gọn biểu thức $\sqrt[3]{{{x^3} + 3{x^2} + 3x + 1}} - \sqrt[3]{{8{x^3} + 12{x^2} + 6x + 1}}$ ta được
-
A.
$x$
-
B.
$ - x$
-
C.
$2x$
-
D.
$ - 2x$
Giải phương trình \(\sqrt {2{x^2} - 4x + 5} = x - 2\) ta được nghiệm là
-
A.
\(x = 1\)
-
B.
\(x = 3\)
-
C.
\(x = 2\)
-
D.
Phương trình vô nghiệm
Cho biểu thức $P = 1:\left( {\dfrac{{x + 2}}{{x\sqrt x - 1}} + \dfrac{{\sqrt x + 1}}{{x + \sqrt x + 1}} - \dfrac{{\sqrt x + 1}}{{x - 1}}} \right)$ . Chọn câu đúng.
-
A.
\(P = \dfrac{{x + \sqrt x + 1}}{{\sqrt x }}\)
-
B.
\(P < 3\)
-
C.
\(P > 3\)
-
D.
Cả A, C đều đúng.
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 3cm,\,AC = 4cm,\,\) đường cao \(AH\) và đường trung tuyến \(AM\). Độ dài đoạn thẳng \(HM\) là
-
A.
\(HM = \dfrac{7}{{10}}cm\)
-
B.
\(HM = \dfrac{9}{5}cm\)
-
C.
\(HM = \dfrac{{43}}{{10}}cm\)
-
D.
\(HM = \dfrac{5}{2}cm\)
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) có \(AC = 15\,cm,\,CH = 6\,cm\). Tính tỉ số lượng giác \(\cos B\).
-
A.
\(\cos B = \dfrac{5}{{\sqrt {21} }}\)
-
B.
\(\cos B = \dfrac{{\sqrt {21} }}{5}\)
-
C.
\(\cos B = \dfrac{2}{5}\)
-
D.
\(\cos B = \dfrac{3}{5}\)
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(CH = 4\,cm,\,BH = 3\,cm.\) Tính tỉ số lượng giác $\cos C$ (làm tròn đến chữ số thập phân thứ $2$ )
-
A.
$\cos C \approx 0,76$
-
B.
$\cos C \approx 0,77$
-
C.
$\cos C \approx 0,75$
-
D.
$\cos C \approx 0,78$
Cho tam giác \(ABC\) cân tại \(A,\,\,\angle B = {65^0},\) đường cao \(CH = 3,6\). Hãy giải tam giác \(ABC\).
-
A.
\(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 5,6\,\,;\,\,BC = 8,52\)
-
B.
\(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 5,6\,\,;\,\,BC = 4,42\)
-
C.
\(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 4,7\,\,;\,\,BC = 4,24\)
-
D.
\(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 4,7\,\,;\,\,BC = 3,97\)
Cho hình thang \(ABCD\) vuông tại \(A\) và \(D;\)\(\angle C = {50^0}\). Biết \(AB = 2;AD = 1,2\). Tính diện tích hình thang \(ABCD.\)
-
A.
\({S_{ABCD}} = 2\,\,\,\left( {đvdt} \right)\)
-
B.
\({S_{ABCD}} = 3\,\,\,\left( {đvdt} \right)\)
-
C.
\({S_{ABCD}} = 4\,\,\,\left( {đvdt} \right)\)
-
D.
\({S_{ABCD}} = \dfrac{5}{2}\,\,\,\left( {đvdt} \right)\)
Hai bạn học sinh Mai và Đào đang đứng ở mặt đất bằng phẳng, cách nhau \(150m\) thì nhìn thấy một chiếc diều ( ở vị trí \(C\) giữa hai bạn). Biết góc ''nâng'' để nhìn thấy diều ở vị trí của Mai là \({45^0}\), góc ''nâng'' để nhìn thấy diều ở vị trí của Đào là \({35^0}\) . Hãy tính độ cao của diều lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(86\,m\)
-
B.
\(89\,m\)
-
C.
\(80\,m\)
-
D.
\(88,22\,m\)
Tính giá trị của \(A =\dfrac{1}{{2\sqrt 1 + 1\sqrt 2 }} + \dfrac{1}{{3\sqrt 2 + 2\sqrt 3 }} + ... + \dfrac{1}{{2018\sqrt {2017} + 2017\sqrt {2018} }}\)
-
A.
\(A=1-\dfrac{2}{\sqrt{2018}}\)
-
B.
\(A=1-\dfrac{1}{\sqrt{2028}}\)
-
C.
\(A=1-\dfrac{1}{\sqrt{2015}}\)
-
D.
\(A=1-\dfrac{1}{\sqrt{2018}}\)
Cho hai tam giác vuông \(OAB\) và \(OCD\) như hình vẽ. Biết \(OB = CD = a\), \(AB = OD = b.\) Tính \(\cos \angle AOC\) theo \(a\) và \(b\).
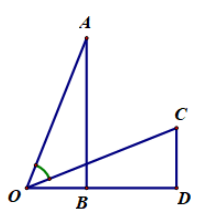
-
A.
\(\dfrac{{2ab}}{{{a^2} + {b^2}}}\).
-
B.
\(\dfrac{{{b^2} - {a^2}}}{{{a^2} + {b^2}}}\).
-
C.
\(1\).
-
D.
\(\dfrac{{{a^2} - {b^2}}}{{{a^2} + {b^2}}}\).
Tính giá trị biểu thức \(A = \dfrac{1}{{1 + \sqrt 3 }} + \dfrac{1}{{\sqrt 3 + \sqrt 5 }} + \dfrac{1}{{\sqrt 5 + \sqrt 7 }} \)\(+ ... + \dfrac{1}{{\sqrt {2019} + \sqrt {2021} }}\)
-
A.
\(1 - \sqrt {2021} \)
-
B.
\(\sqrt {2021} - 1\)
-
C.
\(\dfrac{{\sqrt {2021} - 1}}{2}\)
-
D.
\(\dfrac{{\sqrt {2019} - 1}}{2}\)
Tính diện tích một tam giác vuông có chu vi \(72\,cm\), hiệu giữa đường trung tuyến và đường cao ứng với cạnh huyền bằng \(7\,cm.\)
-
A.
\(100\,c{m^2}\)
-
B.
\(44\,c{m^2}\)
-
C.
\(144\,c{m^2}\)
-
D.
\(24\,c{m^2}\)
Cho đoạn thẳng $AB = 2a$ và trung điểm $O$ của nó. Trên nửa mặt phẳng bờ $AB$ vẽ các tia $Ax,By\;$ vuông góc với $AB.$ Qua \(O\) vẽ một tia cắt tia \(Ax\) tại $M$ sao cho $\widehat {AOM} = \alpha < {90^0}$ . Qua $O$ vẽ tia thứ hai cắt tia $By$ tại $N$ sao cho \(\widehat {MON} = 90^\circ \) . Khi đó, diện tích tam giác \(MON\) là
-
A.
\(\dfrac{{{a^2}}}{{2\sin \alpha .\cos \alpha }}\)
-
B.
\(\dfrac{{{a^2}}}{{\sin \alpha .\cos \alpha }}\)
-
C.
\(\dfrac{a}{{2\sin \alpha .\cos \alpha }}\)
-
D.
\(\dfrac{{2{a^2}}}{{\sin \alpha .\cos \alpha }}\)
Tìm giá trị nhỏ nhất của biểu thức \(A = \dfrac{{x + \sqrt x + 4}}{{\sqrt x }}\) với \(x > 0\)
-
A.
\(5\)
-
B.
\(9\)
-
C.
\(4\)
-
D.
\(0\)
Lời giải và đáp án
Cho tam giác $MNP$ vuông tại $M$. Khi đó $\cos \widehat {MNP}$ bằng

-
A.
$\dfrac{{MN}}{{NP}}$
-
B.
$\dfrac{{MP}}{{NP}}$
-
C.
$\dfrac{{MN}}{{MP}}$
-
D.
$\dfrac{{MP}}{{MN}}$
Đáp án : A
Ta có $\cos \widehat {MNP} = \dfrac{{MN}}{{NP}}$
Cho tam giác $ABC$ vuông tại $A$ có $AB = 3cm,{\rm{ }}BC = 5cm.{\rm{ }}AH$ là đường cao. Tính $BH,CH,AC$ và $AH.$
-
A.
\(BH = 2\,cm\) , \(CH = 3,2\,cm\) , \(AC = 4\,cm\), \(AH = 2,4\,cm\)
-
B.
\(BH = 1,8\,cm\), \(CH = 3,2\,cm\), \(AC = 4\,cm\), \(AH = 2,4\,cm\).
-
C.
\(BH = 1,8\,cm\), \(CH = 3,2\,cm\), \(AC = 3\,cm\), \(AH = 2,4\,cm\)
-
D.
\(BH = 1,8\,cm\), \(CH = 3,2\,cm\), \(AC = 4\,cm\), \(AH = 4,2\,cm\)
Đáp án : B
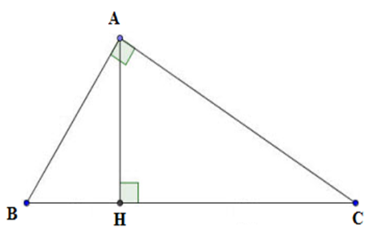
Xét tam giác \(ABC\) vuông tại \(A.\)
+ Theo định lý Pytago ta có \(A{B^2} + A{C^2} = B{C^2} \Leftrightarrow A{C^2} = {5^2} - {3^2} \Rightarrow AC = 4cm\)
+ Theo hệ thức lượng trong tam giác vuông ta có
\(A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{3^2}}}{5} = \dfrac{9}{5} = 1,8cm\)
Mà \(BH + CH = BC \Rightarrow CH = BC - BH = 5 - 1,8 = 3,2\,cm.\)
Lại có \(AH.BC = AB.AC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{3.4}}{5} = 2,4cm\)
Vậy \(BH = 1,8\,cm\), \(CH = 3,2\,cm\), \(AC = 4\,cm\), \(AH = 2,4\,cm\)
Tính \(x\) trong hình vẽ sau:

-
A.
\(x = 14\)
-
B.
\(x = 13\)
-
C.
\(x = 12\)
-
D.
\(x = \sqrt {145} \)
Đáp án : C
Tính \(x\) theo hệ thức lượng \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)\( \Rightarrow AH = \dfrac{{AB.AC}}{{\sqrt {A{B^2} + A{C^2}} }} = \dfrac{{15.20}}{{\sqrt {{{15}^2} + {{20}^2}} }} = 12\)
Vậy \(x = 12\).
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) (như hình vẽ). Hệ thức nào sau đây là sai ?

-
A.
\({b^2} = b'.a\)
-
B.
\(\dfrac{1}{{{h^2}}} = \dfrac{1}{{{c^2}}} + \dfrac{1}{{{b^2}}}\)
-
C.
\(a.h = b'.c'\)
-
D.
\({h^2} = b'.c'\)
Đáp án : C
Nhận thấy \(ah = bc\) nên phương án C là sai.
Cho tam giác \(ABC\) vuông tại \(A,\) chiều cao \(AH\). Chọn câu sai.
-
A.
\(A{H^2} = BH.CH\)
-
B.
\(A{B^2} = BH.BC\)
-
C.
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)
-
D.
\(AH.AB = BC.AC\)
Đáp án : D
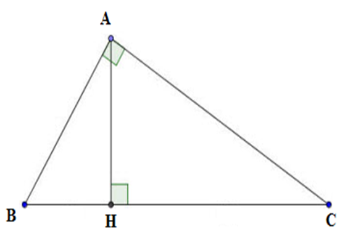
Ta thấy \(AH.BC = AB.AC\) nên D sai.
Khẳng định nào sau đây là sai ?
-
A.
\(a > b \Leftrightarrow \sqrt[3]{a} > \sqrt[3]{b}\)
-
B.
\(a < b \Leftrightarrow \sqrt[3]{a} < \sqrt[3]{b}\)
-
C.
\(a \ge b \Leftrightarrow \sqrt[3]{a} \ge \sqrt[3]{b}\)
-
D.
\(a < b \Leftrightarrow \sqrt[3]{a} > \sqrt[3]{b}\)
Đáp án : D
Với mọi \(a,b\) ta có \(\sqrt[3]{a} > \sqrt[3]{b} \Leftrightarrow a > b;\)\(a \ge b \Leftrightarrow \sqrt[3]{a} \ge \sqrt[3]{b};a < b \Leftrightarrow \sqrt[3]{a} < \sqrt[3]{b}\)
Suy ra A,B,C đúng, D sai.
Khẳng định nào sau đây là đúng ?
-
A.
\(\sqrt {2018 + 2019} = \sqrt {2018} + \sqrt {2019} \)
-
B.
\(\sqrt {2018. 2019} = \dfrac{{\sqrt {2018} }}{{\sqrt {2019} }}\)
-
C.
\(\sqrt {2018} .\sqrt {2019} = \sqrt {2018.2019} \)
-
D.
\(2018. 2019 = \dfrac{{\sqrt {2019} }}{{\sqrt {2018} }}\)
Đáp án : C
Sử dụng công thức khai phương một tích: Với hai số \(a,b\) không âm, ta có \(\sqrt {ab} = \sqrt a .\sqrt b \)
Ta có: \(\sqrt {2018} .\sqrt {2019} = \sqrt {2018.2019} \)
Giá trị của biểu thức \(\sqrt {32} + \sqrt {50} - 3\sqrt 8 - \sqrt {18} \) là
-
A.
$1$
-
B.
$0$
-
C.
$2$
-
D.
$3$
Đáp án : B
-Sử dụng công thức khai phương một tích \(\sqrt {AB} = \sqrt A .\sqrt B ,\,\,\left( {A,B \ge 0} \right)\) đưa biểu thức về các căn thức cùng loại (cùng biểu thức dưới dấu căn).
-Cộng trừ các căn thức
\(\sqrt {32} + \sqrt {50} - 3\sqrt 8 - \sqrt {18} \)\( = \sqrt {16.2} + \sqrt {25.2} - 3\sqrt {4.2} - \sqrt {9.2} \)
\(= 4\sqrt 2 + 5\sqrt 2 - 6\sqrt 2 - 3\sqrt 2 = 0\)
Tìm điều kiện xác định của\(\sqrt {125 - 5x} \).
-
A.
\(x \le 15\)
-
B.
\(x \ge 25\)
-
C.
\(x \le 25\)
-
D.
\(x \ge 0\)
Đáp án : C
Sử dụng điều kiện để \(\sqrt A \) có nghĩa. Ta có \(\sqrt A \) có nghĩa khi \( A \ge 0\).
Ta có: \(\sqrt {125 - 5x} \) có nghĩa khi
\(125 - 5x \ge 0 \\ 5x \le 125 \\ x \le 25\).
Đưa thừa số $\sqrt {81{{\left( {2 - y} \right)}^4}} $ ra ngoài dấu căn ta được ?
-
A.
$9\left( {2 - y} \right)$
-
B.
$81{\left( {2 - y} \right)^2}$
-
C.
$9{\left( {2 - y} \right)^2}$
-
D.
$ - 9{\left( {2 - y} \right)^2}$
Đáp án : C
Sử dụng công thức đưa thừa số ra ngoài dấu căn: Với hai biểu thức $A,B$ mà $B \ge 0$, ta có $\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,{\rm{khi}}\,\,A \ge 0\\ - A\sqrt B \,{\rm{khi}}\,A < 0\end{array} \right.$
Ta có $\sqrt {81{{\left( {2 - y} \right)}^4}} = \sqrt {81.{{\left[ {{{\left( {2 - y} \right)}^2}} \right]}^2}} = \left| {{{\left( {2 - y} \right)}^2}} \right|\sqrt {81} = 9{\left( {2 - y} \right)^2}$
Cạnh bên của tam giác \(ABC\) cân tại \(A\) dài $20cm$ , góc ở đáy là \(50^\circ \) Độ dài cạnh đáy của tam giác cân là (Kết quả làm tròn đến chữ số thập phân thứ nhất).
-
A.
\(25\,cm\)
-
B.
\(25,7\,cm\)
-
C.
\(26\,cm\)
-
D.
\(12,9\,cm\)
Đáp án : B
+ Kẻ đường cao \(AH.\)
+ Tính \(HB\) dựa vào quan hệ giữa cạnh và góc trong tam giác vuông
+ Lập luận dựa vào tính chất tam giác cân để tính cạnh đáy \(BC.\)
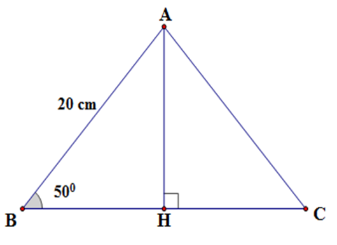
Kẻ \(AH \bot BC\) tại \(H.\) Suy ra \(H\) là trung điểm của \(BC\) (do tam giác \(ABC\) cân tại \(A\) có \(AH\) vừa là đường cao vừa là đường trung tuyến)
Xét tam giác \(AHB\) vuông tại \(H\) có \(\cos \widehat {ABH} = \dfrac{{BH}}{{AB}} \Rightarrow BH = AB.\cos \widehat {ABH}\)\( = 20.\cos 50^\circ \)
Mà \(H\) là trung điểm của \(BC\) nên \(BC = 2BH = 2.2.\cos 50^0\approx 25,7\,cm\)
Vậy \(BC \approx 25,7\,cm.\)
Một cầu trượt trong công viên có độ dốc là ${28^0}$ và có độ cao là $2,1m.$Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ hai).
-
A.
$3,95\,m$
-
B.
$3,8\,m$
-
C.
$4,5\,m$
-
D.
$4,47\,m$
Đáp án : D
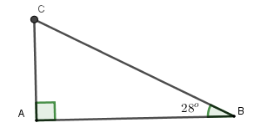
Ta có độ dài của mặt cầu trượt là $AB$; $AC = 2,1\,m$ và $\widehat {ABC} = 28^\circ $
Xét tam giác $ACB$ vuông tại $A$ có
$BC = AB:\sin B = 2,1:\sin 28^\circ \simeq 4,47\,m$
Vậy độ dài của mặt cầu trượt là $4,47\,m.$
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 10\,cm,\widehat C = 30^\circ .\) Tính $AB;BC$
-
A.
$AB = \dfrac{{5\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$
-
B.
$AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{14\sqrt 3 }}{3}$
-
C.
$AB = \dfrac{{10\sqrt 3 }}{3};BC = 20\sqrt 3 $
-
D.
$AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$
Đáp án : D
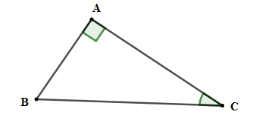
Xét tam giác \(ABC\) vuông tại \(A\) có
$\tan C = \dfrac{{AB}}{{AC}} \Rightarrow AB = AC.\tan C = 10.\tan 30^\circ = \dfrac{{10\sqrt 3 }}{3}$; $\cos C = \dfrac{{AC}}{{BC}} \Rightarrow BC = \dfrac{{AC}}{{\cos C}} = \dfrac{{10}}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{20\sqrt 3 }}{3}$
Vậy $AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$.
Một cột đèn có bóng trên mặt đất dài \(6m.\) Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng \({38^0}.\) Tính chiều cao của cột đèn. (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(4,6\,m\)
-
B.
\(4,69\,m\)
-
C.
\(5,7\,m\)
-
D.
\(6,49\,m\)
Đáp án : B
Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông
Cạnh góc vuông = tích cạnh góc vuông còn lại với tan góc đối.
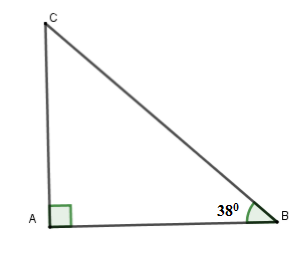
Ta có chiều cao cột đèn là \(AC\); \(AB = 6\,m\) và \(\widehat {ACB} = 38^\circ \)
Xét tam giác \(ACB\) vuông tại \(A\) có
\(AC = AB.\tan B = 6.\tan 38^\circ \approx 4,69\,\,m\)
Vậy cột đèn cao \(4,69\,m\)
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là đúng ?

-
A.
$A{H^2} = AB.AC$
-
B.
$A{H^2} = BH.CH$
-
C.
$A{H^2} = AB.BH$
-
D.
$A{H^2} = CH.BC$
Đáp án : B
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ . Khi đó ta có hệ thức $H{A^2} = HB.HC$
Chọn đáp án đúng.
-
A.
\(\dfrac{4}{{\sqrt 3 + 1}} + \dfrac{1}{{\sqrt 3 - 2}} + \dfrac{6}{{\sqrt 3 - 3}} = - 7 - \sqrt 3 \)
-
B.
\(\dfrac{4}{{\sqrt 3 + 1}} + \dfrac{1}{{\sqrt 3 - 2}} + \dfrac{6}{{\sqrt 3 - 3}} = 7\)
-
C.
\(\dfrac{4}{{\sqrt 3 + 1}} + \dfrac{1}{{\sqrt 3 - 2}} + \dfrac{6}{{\sqrt 3 - 3}} = - 7\)
-
D.
\(\dfrac{4}{{\sqrt 3 + 1}} + \dfrac{1}{{\sqrt 3 - 2}} + \dfrac{6}{{\sqrt 3 - 3}} = 7 + 7\sqrt 3 \)
Đáp án : C
Sử dụng công thức : Với \(A > 0\) và \(A \ne {B^2}\) thì \(\dfrac{C}{{\sqrt A \pm B}} = \dfrac{{C(\sqrt A \mp B)}}{{A - {B^2}}}\)
Ta có \(\dfrac{4}{{\sqrt 3 + 1}} + \dfrac{1}{{\sqrt 3 - 2}} + \dfrac{6}{{\sqrt 3 - 3}}\)\( = \dfrac{{4\left( {\sqrt 3 - 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}} + \dfrac{{1\left( {\sqrt 3 + 2} \right)}}{{\left( {\sqrt 3 + 2} \right)\left( {\sqrt 3 - 2} \right)}} + \dfrac{{6\left( {\sqrt 3 + 3} \right)}}{{\left( {\sqrt 3 + 3} \right)\left( {\sqrt 3 - 3} \right)}}\)
\( = \dfrac{{4\left( {\sqrt 3 - 1} \right)}}{{{{\left( {\sqrt 3 } \right)}^2} - {1^2}}} + \dfrac{{\sqrt 3 + 2}}{{{{\left( {\sqrt 3 } \right)}^2} - {2^2}}} + \dfrac{{6\left( {\sqrt 3 + 3} \right)}}{{{{\left( {\sqrt 3 } \right)}^2} - {3^2}}}\) \( = \dfrac{{4\left( {\sqrt 3 - 1} \right)}}{{3 - 1}} + \dfrac{{\sqrt 3 + 2}}{{3 - 4}} + \dfrac{{6\left( {\sqrt 3 + 3} \right)}}{{3 - 9}}\)
\( = \dfrac{{4\left( {\sqrt 3 - 1} \right)}}{2} + \dfrac{{\sqrt 3 + 2}}{{\left( { - 1} \right)}} + \dfrac{{6\left( {\sqrt 3 + 3} \right)}}{{\left( { - 6} \right)}}\) \( = 2\left( {\sqrt 3 - 1} \right) - \sqrt 3 - 2 - \sqrt 3 - 3 = - 7.\)
Khẳng định nào sau đây là đúng?
-
A.
$\sqrt {{A^2}} = A\,\,\,khi\,\,A < 0$
-
B.
$\sqrt {{A^2}} = - A\,\,\,khi\,\,A \ge 0$
-
C.
$\sqrt A < \sqrt B \,\,\, \Leftrightarrow \,\,0 \le A < B$
-
D.
$A > B \Leftrightarrow \sqrt A < \sqrt B $
Đáp án : C
Sử dụng hằng đẳng thức $\sqrt {{A^2}} = \left| A \right|$ và cách so sánh hai căn bậc hai.
- Với $A,B$ không âm ta có $A < B $ hay $ \sqrt A < \sqrt B $ nên C đúng, D sai.
- Ta có hằng đẳng thức $\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}\,\,\,\,A\,\,\,\,\,{\rm{khi}}\,\,\,A \ge 0\\ - A\,\,\,\,\,\,{\rm{khi}}\,\,\,A < 0\end{array} \right.$ nên A, B sai.
Cho tam giác $MNP$ vuông tại $N$. Hệ thức nào sau đây là đúng ?
-
A.
$MN = MP.\sin P$
-
B.
$MN = MP.\cos P$
-
C.
$MN = MP.\tan P$
-
D.
$MN = MP.\cot P$
Đáp án : A
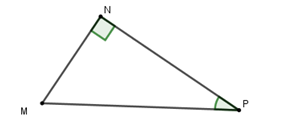
Ta có $\sin P = \dfrac{{MN}}{{MP}} \Rightarrow MN = MP.\sin P$.
Tìm giá trị của \(x\) không âm biết \(5\sqrt {2x} - 125 = 0\).
-
A.
\(x = \dfrac{{25}}{2}\)
-
B.
\(x = 125\)
-
C.
\(x = 25\)
-
D.
\(x = \dfrac{{625}}{2}\)
Đáp án : D
Đưa phương trình chứa căn về dạng \(\sqrt A = B\) và sử dụng cách giải
\(\sqrt A = B \\ \left\{ \begin{array}{l}B \ge 0\\A = {B^2}\end{array} \right.\).
Điều kiện: \(2x \ge 0 \) hay \(x \ge 0\)
Ta có:
\(5\sqrt {2x} - 125 = 0 \\ 5\sqrt {2x} = 125 \\ \sqrt {2x} = 25\) mà \(25 > 0\) nên
\(\sqrt {2x} = 25 \\ 2x = {25^2} \\ 2x = 625 \\ x = \dfrac{{625}}{2}\) (thỏa mãn).
Vậy \(x = \dfrac{{625}}{2}\).
Rút gọn biểu thức \(\dfrac{{{a^2}}}{{11}}.\sqrt {\dfrac{{121}}{{{a^4}{b^{10}}}}} \) với \(ab \ne 0\) ta được:
-
A.
\(\dfrac{1}{{\left| {{b^5}} \right|}}\)
-
B.
\(\dfrac{1}{{{b^5}}}\)
-
C.
\({b^5}\)
-
D.
\(\dfrac{{11}}{{{b^5}}}\)
Đáp án : A
Sử dụng công thức khai phương một tích: Với hai số \(a,b\) không âm, ta có \(\sqrt {ab} = \sqrt a .\sqrt b \)
Sử dụng công thức khai phương một thương: Với số \(a\) không âm và số \(b\) dương, ta có \(\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}\).
Sử dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\)
Ta có: \(\dfrac{{{a^2}}}{{11}}.\sqrt {\dfrac{{121}}{{{a^4}{b^{10}}}}} \)\(\dfrac{{{a^2}}}{{11}}.\dfrac{{\sqrt {121} }}{{\sqrt {{a^4}} .\sqrt {{b^{10}}} }} = \dfrac{{{a^2}}}{{11}}.\dfrac{{\sqrt {{{11}^2}} }}{{\sqrt {{{\left( {{a^2}} \right)}^2}} .\sqrt {{{\left( {{b^5}} \right)}^2}} }} = \dfrac{{{a^2}}}{{11}}.\dfrac{{11}}{{{a^2}.\left| {{b^5}} \right|}} = \dfrac{1}{{\left| {{b^5}} \right|}}\).
Trục căn thức ở mẫu biểu thức \(\dfrac{4}{{3\sqrt x + 2\sqrt y }}\) với \(x \ge 0;y \ge 0;x \ne \dfrac{4}{9}y\) ta được:
-
A.
\(\dfrac{{3\sqrt x - 2\sqrt y }}{{9x - 4y}}\)
-
B.
\(\dfrac{{12\sqrt x - 8\sqrt y }}{{3x + 2y}}\)
-
C.
\(\dfrac{{12\sqrt x + 8\sqrt y }}{{9x + 4y}}\)
-
D.
\(\dfrac{{12\sqrt x - 8\sqrt y }}{{9x - 4y}}\)
Đáp án : D
Sử dụng công thức
Với các biểu thức \(A,B,C\) mà \(A \ge 0,B \ge 0,A \ne B\) ta có:
\(\dfrac{C}{{\sqrt A - \sqrt B }} = \dfrac{{C\left( {\sqrt A + \sqrt B } \right)}}{{A - B}}\); \(\dfrac{C}{{\sqrt A + \sqrt B }} = \dfrac{{C\left( {\sqrt A - \sqrt B } \right)}}{{A - B}}\)
Ta có: \(\dfrac{4}{{3\sqrt x + 2\sqrt y }}\)\( = \dfrac{{4\left( {3\sqrt x - 2\sqrt y } \right)}}{{\left( {3\sqrt x + 2\sqrt y } \right)\left( {3\sqrt x - 2\sqrt y } \right)}} = \dfrac{{4\left( {3\sqrt x - 2\sqrt y } \right)}}{{{{\left( {3\sqrt x } \right)}^2} - {{\left( {2\sqrt y } \right)}^2}}} = \dfrac{{12\sqrt x - 8\sqrt y }}{{9x - 4y}}\)
Rút gọn biểu thức \(2\sqrt {8\sqrt 3 } - 2\sqrt {5\sqrt 3 } - 3\sqrt {20\sqrt 3 } \)
-
A.
\(0\)
-
B.
\(4\sqrt {2\sqrt 3 } - 8\sqrt {5\sqrt 3 } \)
-
C.
\(\dfrac{3}{2}\sqrt 5 \)
-
D.
\(1\)
Đáp án : B
Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\)
\(\begin{array}{l}\,\,\,\,\,2\sqrt {8\sqrt 3 } - 2\sqrt {5\sqrt 3 } - 3\sqrt {20\sqrt 3 } \\ = 2\sqrt {4.2} .\sqrt {\sqrt 3 } - 2\sqrt 5 .\sqrt {\sqrt 3 } - 3\sqrt {4.5} .\sqrt {\sqrt 3 } \\ = 2.2\sqrt 2 \sqrt {\sqrt 3 } - 2\sqrt 5 \sqrt {\sqrt 3 } - 3.2.\sqrt 5 .\sqrt {\sqrt 3 } \\ = 4\sqrt {2\sqrt 3 } - \left( {2 + 3.2} \right)\sqrt 5 \sqrt {\sqrt 3 } \\ = 4\sqrt {2\sqrt 3 } - 8\sqrt {5\sqrt 3 } \end{array}\)
Rút gọn biểu thức \(3\sqrt {8a} + \dfrac{1}{4}\sqrt {\dfrac{{32a}}{{25}}} - \dfrac{a}{{\sqrt 3 }}.\sqrt {\dfrac{3}{{2a}}} - \sqrt {2a} \) với \(a > 0\) ta được:
-
A.
\(\dfrac{{47}}{{10}}\sqrt a \)
-
B.
\(\dfrac{{21}}{5}\sqrt a \)
-
C.
\(\dfrac{{47}}{{10}}\sqrt {2a} \)
-
D.
\(\dfrac{{47}}{5}\sqrt {2a} \)
Đáp án : C
- Khử mẫu biểu thức lấy căn theo công thức \(\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt {AB} }}{B}\,\left( {A \ge 0,B > 0} \right)\)
- Sử dụng công thức khai phương một thương \(\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt A }}{{\sqrt B }}\) với \(A \ge 0,B > 0\) và công thức khai phương một tích \(\sqrt {AB} = \sqrt A .\sqrt B ,\,\,\left( {A,B \ge 0} \right)\)
- Cộng trừ các căn thức bậc hai.
\(3\sqrt {8a} + \dfrac{1}{4}\sqrt {\dfrac{{32a}}{{25}}} - \dfrac{a}{{\sqrt 3 }}.\sqrt {\dfrac{3}{{2a}}} - \sqrt {2a} \) \( = 3\sqrt {4.2a} + \dfrac{1}{4}\dfrac{{\sqrt {16.2a} }}{{\sqrt {25} }} - \dfrac{a}{{\sqrt 3 }}.\dfrac{{\sqrt 3 }}{{\sqrt {2a} }} - \sqrt {2a} \) \( = 3.2\sqrt {2a} + \dfrac{1}{4}.\dfrac{{4\sqrt {2a} }}{5} - \dfrac{a}{{\sqrt 3 }}.\dfrac{{\sqrt 3 .\sqrt {2a} }}{{2a}} - \sqrt {2a} \) \( = 6\sqrt {2a} + \dfrac{1}{5}\sqrt {2a} - \dfrac{1}{2}\sqrt {2a} - \sqrt {2a} \)
\( = \sqrt {2a} .\left( {6 + \dfrac{1}{5} - \dfrac{1}{2} - 1} \right) = \dfrac{{47}}{{10}}\sqrt {2a} \)
Cho biểu thức \(A = \dfrac{{\sqrt x + 1}}{{\sqrt x - 2}}\) với \(x \ge 0;x \ne 4\). Tìm các giá trị của \(x\) biết \(A = \dfrac{{\sqrt x - 1}}{2}\) .
-
A.
\(x = 0;x = 5\)
-
B.
\(x = 0\)
-
C.
\(x = 0;x = 25\)
-
D.
\(x = 5;x = 1\)
Đáp án : C
Cho \(A = \dfrac{{\sqrt x - 1}}{2}\)
Giải phương trình chứa căn bằng cách quy đồng mẫu số, đưa phương trình về dạng chứa căn cơ bản đã biết.
Với \(x \ge 0;x \ne 4\) ta có: \(A = \dfrac{{\sqrt x - 1}}{2} \\ \dfrac{{\sqrt x + 1}}{{\sqrt x - 2}} = \dfrac{{\sqrt x - 1}}{2}\)
\( \Rightarrow 2\left( {\sqrt x + 1} \right) = \left( {\sqrt x - 2} \right)\left( {\sqrt x - 1} \right) \\ 2\sqrt x + 2 = x - 3\sqrt x + 2\)
\( \\ x - 5\sqrt x = 0 \\ \sqrt x \left( {\sqrt x - 5} \right) = 0 \\ \left[ \begin{array}{l}\sqrt x = 0\\\sqrt x = 5\end{array} \right. \\ \left[ \begin{array}{l}x = 0\left( {tm} \right)\\x = 25\left( {tm} \right)\end{array} \right.\)
Vậy giá trị cần tìm là \(x = 0;x = 25\).
Kết luận nào đúng khi nói về nghiệm của phương trình $\sqrt[3]{{3x - 2}} = - 2$
-
A.
Là số nguyên âm
-
B.
Là phân số
-
C.
Là số vô tỉ
-
D.
Là số nguyên dương
Đáp án : A
- Áp dụng $\sqrt[3]{x} = a$ thì $ x = {a^3}$
Ta có $\sqrt[3]{{3x - 2}} = - 2$
$ 3x - 2 = {\left( { - 2} \right)^3} \\ 3x - 2 = - 8 \\ 3x = - 6 \\ x = - 2$
Do đó nghiệm của phương trình là một số nguyên âm.
Thu gọn biểu thức $\sqrt[3]{{{x^3} + 3{x^2} + 3x + 1}} - \sqrt[3]{{8{x^3} + 12{x^2} + 6x + 1}}$ ta được
-
A.
$x$
-
B.
$ - x$
-
C.
$2x$
-
D.
$ - 2x$
Đáp án : B
- Đưa biểu thức dưới dấu căn về hằng đẳng thức ${\left( {a + b} \right)^3} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}$
-Áp dụng $\sqrt[3]{{{a^3}}} = a$
Ta có $\sqrt[3]{{{x^3} + 3{x^2} + 3x + 1}} - \sqrt[3]{{8{x^3} + 12{x^2} + 6x + 1}}$$ = \sqrt[3]{{{{\left( {x + 1} \right)}^3}}} - \sqrt[3]{{{{\left( {2x + 1} \right)}^3}}}$
$= x + 1 - 2x - 1 = - x$.
Giải phương trình \(\sqrt {2{x^2} - 4x + 5} = x - 2\) ta được nghiệm là
-
A.
\(x = 1\)
-
B.
\(x = 3\)
-
C.
\(x = 2\)
-
D.
Phương trình vô nghiệm
Đáp án : D
+ Tìm điều kiện
+ Giải phương trình dạng \(\sqrt A = B\,\left( {B \ge 0} \right) \Leftrightarrow A = {B^2}\)
Điều kiện:
\(x - 2 \ge 0 \Leftrightarrow x \ge 2.\)
Ta có: \(\sqrt {2{x^2} - 4x + 5} = x - 2\)\( \Leftrightarrow 2{x^2} - 4x + 5 = {\left( {x - 2} \right)^2}\)
\( \Leftrightarrow 2{x^2} - 4x + 5 = {x^2} - 4x + 4 \Leftrightarrow {x^2} + 1 = 0\) \( \Leftrightarrow {x^2} = - 1\,\) (vô nghiệm vì \({x^2} \ge 0\,\,\forall x\) )
Vậy phương trình vô nghiệm.
Cho biểu thức $P = 1:\left( {\dfrac{{x + 2}}{{x\sqrt x - 1}} + \dfrac{{\sqrt x + 1}}{{x + \sqrt x + 1}} - \dfrac{{\sqrt x + 1}}{{x - 1}}} \right)$ . Chọn câu đúng.
-
A.
\(P = \dfrac{{x + \sqrt x + 1}}{{\sqrt x }}\)
-
B.
\(P < 3\)
-
C.
\(P > 3\)
-
D.
Cả A, C đều đúng.
Đáp án : D
+ Tìm điều kiện
+ Phân tích mẫu thức thành nhân tử rồi qui đồng mẫu các phân thức
+ Từ đó rút gọn biểu thức
+ Xét hiệu \(P - 3\) rồi so sánh hiệu đó với \(0\) để so sánh \(P\) với \(3.\)
Điều kiện xác định: \(x \ne 1;x > 0\)
\(\begin{array}{l}P = 1:\left( {\dfrac{{x + 2}}{{x\sqrt x - 1}} + \dfrac{{\sqrt x + 1}}{{x + \sqrt x + 1}} - \dfrac{{\sqrt x + 1}}{{x - 1}}} \right)\\ = 1:\left( {\dfrac{{x + 2}}{{\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}} + \dfrac{{\sqrt x + 1}}{{\left( {x + \sqrt x + 1} \right)}} - \dfrac{{\sqrt x + 1}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}} \right)\\ = 1:\dfrac{{\left( {x + 2} \right)\left( {\sqrt x + 1} \right) + {{\left( {\sqrt x + 1} \right)}^2}\left( {\sqrt x - 1} \right) - \left( {\sqrt x + 1} \right)\left( {x + \sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}\end{array}\)
\( = 1:\dfrac{{x\sqrt x + x + 2\sqrt x + 2 + x\sqrt x + x - \sqrt x - 1 - \left( {x\sqrt x + x + \sqrt x + x + \sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}\)
\(\begin{array}{l} = \dfrac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}{{x\sqrt x - \sqrt x }}\\ = \dfrac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\\ = \dfrac{{x + \sqrt x + 1}}{{\sqrt x }}\end{array}\)
Vậy \(P = \dfrac{{x + \sqrt x + 1}}{{\sqrt x }}\) với \(x \ne 1;x > 0\)
+ So sánh \(P\) với \(3.\)
Xét \(P - 3 = \dfrac{{x + \sqrt x + 1}}{{\sqrt x }} - 3 = \dfrac{{x + \sqrt x + 1 - 3\sqrt x }}{{\sqrt x }} = \dfrac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x }}\)
Với \(x \ne 1;x > 0\) ta có: \(\sqrt x > 0\); $\sqrt x \ne 1$ nên \({\left( {\sqrt x - 1} \right)^2} > 0\) suy ra: $P-3 > 0$ hay $P > 3$
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 3cm,\,AC = 4cm,\,\) đường cao \(AH\) và đường trung tuyến \(AM\). Độ dài đoạn thẳng \(HM\) là
-
A.
\(HM = \dfrac{7}{{10}}cm\)
-
B.
\(HM = \dfrac{9}{5}cm\)
-
C.
\(HM = \dfrac{{43}}{{10}}cm\)
-
D.
\(HM = \dfrac{5}{2}cm\)
Đáp án : A
+) Sử dụng hệ thức lượng trong tam giác vuông tính \(BH\).
+) Tính \(HM = BM - BH\).
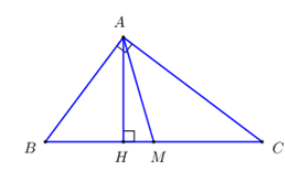
Áp dụng định lí Pytago trong tam giác vuông \(ABC:\,\,BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{3^2} + {4^2}} = 5\,\,\left( {cm} \right)\).
Áp dụng hệ thức lượng trong tam giác vuông \(ABC:\,\,A{B^2} = BC.BH \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{9}{5}\,\,\left( {cm} \right)\).
\(M\) là trung điểm của \(BC \Rightarrow BM = \dfrac{1}{2}BC = \dfrac{5}{2}\,\,\left( {cm} \right)\).
Vậy \( \Rightarrow HM = BM - BH = \dfrac{7}{{10}}\,\,\left( {cm} \right)\)
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) có \(AC = 15\,cm,\,CH = 6\,cm\). Tính tỉ số lượng giác \(\cos B\).
-
A.
\(\cos B = \dfrac{5}{{\sqrt {21} }}\)
-
B.
\(\cos B = \dfrac{{\sqrt {21} }}{5}\)
-
C.
\(\cos B = \dfrac{2}{5}\)
-
D.
\(\cos B = \dfrac{3}{5}\)
Đáp án : B
Bước 1: Tính cạnh cần thiết lại theo định lý Pytago hoặc hệ thức lượng trong tam giác vuông.
Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn. Sử dụng hai góc phụ nhau thì sin góc này bằng cosin góc kia.
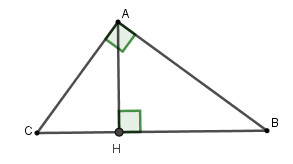
Xét tam giác \(AHC\) vuông tại \(H\), theo định lý Pytago ta có
\(A{H^2} = A{C^2} - C{H^2} = {15^2} - {6^2} = 189 \Rightarrow AH = 3\sqrt {21} \)
\( \Rightarrow \sin C = \dfrac{{AH}}{{AC}} = \dfrac{{3\sqrt {21} }}{{15}} = \dfrac{{\sqrt {21} }}{5}\)
Mà tam giác \(ABC\) vuông tại \(A\) nên \(\widehat B,\widehat C\) là hai góc phụ nhau. Do đó \(\cos B = \sin C = \dfrac{{\sqrt {21} }}{5}.\)
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(CH = 4\,cm,\,BH = 3\,cm.\) Tính tỉ số lượng giác $\cos C$ (làm tròn đến chữ số thập phân thứ $2$ )
-
A.
$\cos C \approx 0,76$
-
B.
$\cos C \approx 0,77$
-
C.
$\cos C \approx 0,75$
-
D.
$\cos C \approx 0,78$
Đáp án : A
Bước 1: Tính cạnh cần thiết lại theo định lý Pytago hoặc hệ thức lượng trong tam giác vuông.
Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn
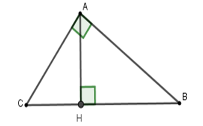
Xét tam giác $ABC$ vuông tại $A$ có $BC = BH + CH = 7\,\,cm$
theo hệ thức lượng trong tam giác vuông ta có $A{C^2} = CH.BC \Rightarrow A{C^2} = 4.7 \Rightarrow AC \approx 5,29\,\,cm$
$ \Rightarrow \cos C = \dfrac{{AC}}{{BC}} = \dfrac{{5,29}}{7} \approx 0,76$.
Cho tam giác \(ABC\) cân tại \(A,\,\,\angle B = {65^0},\) đường cao \(CH = 3,6\). Hãy giải tam giác \(ABC\).
-
A.
\(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 5,6\,\,;\,\,BC = 8,52\)
-
B.
\(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 5,6\,\,;\,\,BC = 4,42\)
-
C.
\(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 4,7\,\,;\,\,BC = 4,24\)
-
D.
\(\angle A = {50^0}\,\,;\,\,\,\angle C = {65^0}\,\,;\,\,AB = AC = 4,7\,\,;\,\,BC = 3,97\)
Đáp án : D
Áp dụng hệ thức về cạnh và góc trong tam giác vuông.
Sử dụng tính chất tam giác cân.
Sử dụng định lý tổng ba góc trong một tam giác.
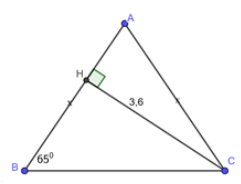
Vì \(\Delta ABC\) là tam giác cân tại \(A\)\( \Rightarrow \angle C = \angle B = {65^0}\)
Ta có \(\angle A + \angle B + \angle C = {180^0}\)(định lý tổng ba góc trong một tam giác)
\( \Rightarrow \angle A = {180^0} - 2\angle C = {180^0} - {2.65^0} = {50^0}\)
Xét \(\Delta ACH\) vuông tại \(H\) ta có:
\(\sin A = \dfrac{{CH}}{{AC}}\) \( \Leftrightarrow \sin {50^0} = \dfrac{{3,6}}{{AC}}\)\( \Rightarrow AC = \dfrac{{3,6}}{{\sin {{50}^0}}} \approx 4,7\)
Vì \(\Delta ABC\) là tam giác cân tại \(A\)\( \Rightarrow AC = AB \approx 4,7\)
Xét \(\Delta BCH\) vuông tại \(H\) ta có:
\(\sin B = \dfrac{{CH}}{{BC}} \Leftrightarrow \sin {65^0} = \dfrac{{3,6}}{{BC}} \)\(\Rightarrow BC = \dfrac{{3,6}}{{\sin {{65}^0}}} \approx 3,97\)
Cho hình thang \(ABCD\) vuông tại \(A\) và \(D;\)\(\angle C = {50^0}\). Biết \(AB = 2;AD = 1,2\). Tính diện tích hình thang \(ABCD.\)
-
A.
\({S_{ABCD}} = 2\,\,\,\left( {đvdt} \right)\)
-
B.
\({S_{ABCD}} = 3\,\,\,\left( {đvdt} \right)\)
-
C.
\({S_{ABCD}} = 4\,\,\,\left( {đvdt} \right)\)
-
D.
\({S_{ABCD}} = \dfrac{5}{2}\,\,\,\left( {đvdt} \right)\)
Đáp án : B
Áp dụng hệ thức về cạnh và góc trong tam giác vuông.
Sử dụng tính chất hình chữ nhật.
Công thức tính diện tích hình thang vuông: \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AD}}{2}.\)
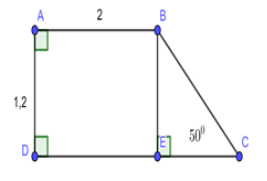
Kẻ \(BE \bot DC,\,\,\,E \in CD.\)
Xét tứ giác \(ABED\) có \(\angle A = \angle D = \angle E = {90^0}\)
\( \Rightarrow ABED\) là hình chữ nhật \( \Rightarrow \left\{ \begin{array}{l}AB = ED = 2\\AD = BE = 1,2\end{array} \right.\)
Xét \(\Delta BCE\) vuông tại \(E\) ta có: \(EC = BE.cot\angle C = 1,2.cot{50^0}\)
\( \Rightarrow DC = DE + EC = 2 + 1,2.\cot {50^0}\)
\( \Rightarrow {S_{ABCD}} = \dfrac{{\left( {AB + CD} \right)AD}}{2}\)\( = \dfrac{{\left( {2 + 2 + 1,2.\cot {{50}^0}} \right).1,2}}{2} \approx 3\,\,\,\,\left( {đvdt} \right).\)
Hai bạn học sinh Mai và Đào đang đứng ở mặt đất bằng phẳng, cách nhau \(150m\) thì nhìn thấy một chiếc diều ( ở vị trí \(C\) giữa hai bạn). Biết góc ''nâng'' để nhìn thấy diều ở vị trí của Mai là \({45^0}\), góc ''nâng'' để nhìn thấy diều ở vị trí của Đào là \({35^0}\) . Hãy tính độ cao của diều lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(86\,m\)
-
B.
\(89\,m\)
-
C.
\(80\,m\)
-
D.
\(88,22\,m\)
Đáp án : D
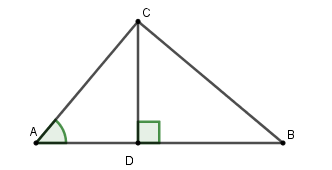
Độ cao của máy bay là \(CD\), độ dài \(AB = 100\,m\). Đào đứng ở \(A\) , Mai đứng ở \(B\) .
Gọi \(AD = x\left( {0 < x < 100} \right) \Rightarrow BD = 150 - x\)
Xét \(\Delta ACD\) vuông tại \(D\) ta có \(CD = AD.\cot A = x.\cot 45^\circ = x\)
Xét \(\Delta ABD\) vuông tại \(D\) ta có \(CD = BD.{\mathop{\rm cotB}\nolimits} = \left( {150 - x} \right).\cot 35^\circ \)
Nên \(x = \left( {150 - x} \right)\cot 35^\circ \Rightarrow x \approx 88,22\) (thoả mãn)
\( \Rightarrow CD = x = 88,22m\)
Vậy độ cao của diều lúc đó so với mặt đất là \(88,22\,m\).
Tính giá trị của \(A =\dfrac{1}{{2\sqrt 1 + 1\sqrt 2 }} + \dfrac{1}{{3\sqrt 2 + 2\sqrt 3 }} + ... + \dfrac{1}{{2018\sqrt {2017} + 2017\sqrt {2018} }}\)
-
A.
\(A=1-\dfrac{2}{\sqrt{2018}}\)
-
B.
\(A=1-\dfrac{1}{\sqrt{2028}}\)
-
C.
\(A=1-\dfrac{1}{\sqrt{2015}}\)
-
D.
\(A=1-\dfrac{1}{\sqrt{2018}}\)
Đáp án : D
Sử dụng: \(\dfrac{1}{{k\sqrt {k - 1} + \left( {k - 1} \right)\sqrt k }} \)\(= \dfrac{1}{{\sqrt {k - 1} }} - \dfrac{1}{{\sqrt k }}\)
Ta có: \(k\sqrt {k - 1} + \left( {k - 1} \right)\sqrt k \, = \sqrt {k\left( {k - 1} \right)} \left( {\sqrt k + \sqrt {k - 1} } \right)\) với \(k \ge 1\).
\(\begin{array}{l} \Rightarrow \dfrac{1}{{k\sqrt {k - 1} + \left( {k - 1} \right)\sqrt k }} \\= \dfrac{1}{{\sqrt {k\left( {k - 1} \right)} \left( {\sqrt k + \sqrt {k - 1} } \right)}} \\= \dfrac{{\left( {\sqrt k - \sqrt {k - 1} } \right)}}{{\sqrt {k\left( {k - 1} \right)} \left( {\sqrt k + \sqrt {k - 1} } \right)\left( {\sqrt k - \sqrt {k - 1} } \right)}}\\ = \dfrac{{\sqrt k - \sqrt {k - 1} }}{{\sqrt {k\left( {k - 1} \right)} }} \\= \dfrac{{\sqrt k - \sqrt {k - 1} }}{{\sqrt k .\sqrt {k - 1} }} \\= \dfrac{1}{{\sqrt {k - 1} }} - \dfrac{1}{{\sqrt k }}\end{array}\)
Thay lại vào A ta được:
\(A = \dfrac{1}{{2\sqrt 1 + 1\sqrt 2 }} + \dfrac{1}{{3\sqrt 2 + 2\sqrt 3 }}\)\( + ... + \dfrac{1}{{2018\sqrt {2017} + 2017\sqrt {2018} }}\)\(= \,\left( {\dfrac{1}{{\sqrt 1 }} - \dfrac{1}{{\sqrt 2 }}} \right) + \left( {\dfrac{1}{{\sqrt 2 }} - \dfrac{1}{{\sqrt 3 }}} \right) \)\(+ ..... + \left( {\dfrac{1}{{\sqrt {2017} }} - \dfrac{1}{{\sqrt {2018} }}} \right)\)\(= 1 - \dfrac{1}{{\sqrt {2018} }}\)
Cho hai tam giác vuông \(OAB\) và \(OCD\) như hình vẽ. Biết \(OB = CD = a\), \(AB = OD = b.\) Tính \(\cos \angle AOC\) theo \(a\) và \(b\).

-
A.
\(\dfrac{{2ab}}{{{a^2} + {b^2}}}\).
-
B.
\(\dfrac{{{b^2} - {a^2}}}{{{a^2} + {b^2}}}\).
-
C.
\(1\).
-
D.
\(\dfrac{{{a^2} - {b^2}}}{{{a^2} + {b^2}}}\).
Đáp án : A
Tách \(\angle AOC = \angle AOB - \angle COD\). Áp dụng công thức cộng lượng giác và Pitago để tính \(\cos \angle AOC\)
Xét \(\Delta OAB\) và \(\Delta COD\) có:
\(\begin{array}{l}\angle OBA = \angle CDO = {90^o}\,\,\,\,\left( {gt} \right)\\OB = CD\,\,\,\left( {gt} \right)\\AB = OD\,\,\,\,\left( {gt} \right)\\ \Rightarrow \Delta OAB = \Delta COD\,\,\,\left( {c - g - c} \right)\end{array}\)
\( \Rightarrow OA = OC\) (2 cạnh tương ứng)
\( \Rightarrow OA.OC = O{A^2} = O{B^2} + A{B^2} = {a^2} + {b^2}\) (Định lý Pytago)
\(\begin{array}{l}\cos \angle AOC = \cos \left( {\angle AOB - \angle COD} \right) = \cos \angle AOB\cos \angle COD + \sin \angle AOB\sin \angle COD\\ = \dfrac{{OB}}{{OA}}.\dfrac{{OD}}{{OC}} + \dfrac{{AB}}{{OA}}.\dfrac{{CD}}{{OC}} = \dfrac{{OB.OD + AB.CD}}{{OA.OC}} = \dfrac{{ab + ab}}{{{a^2} + {b^2}}} = \dfrac{{2ab}}{{{a^2} + {b^2}}}.\end{array}\)
Tính giá trị biểu thức \(A = \dfrac{1}{{1 + \sqrt 3 }} + \dfrac{1}{{\sqrt 3 + \sqrt 5 }} + \dfrac{1}{{\sqrt 5 + \sqrt 7 }} \)\(+ ... + \dfrac{1}{{\sqrt {2019} + \sqrt {2021} }}\)
-
A.
\(1 - \sqrt {2021} \)
-
B.
\(\sqrt {2021} - 1\)
-
C.
\(\dfrac{{\sqrt {2021} - 1}}{2}\)
-
D.
\(\dfrac{{\sqrt {2019} - 1}}{2}\)
Đáp án : C
- Áp dụng: \(\dfrac{1}{{\sqrt a + \sqrt b }} = \dfrac{{\sqrt a - \sqrt b }}{{a - b}}\) với \(a , b>0\)
Ta có:
\(A = \dfrac{1}{{1 + \sqrt 3 }} + \dfrac{1}{{\sqrt 3 + \sqrt 5 }} + \dfrac{1}{{\sqrt 5 + \sqrt 7 }} \)\(+ ... + \dfrac{1}{{\sqrt {2019} + \sqrt {2021} }}\)\(= \dfrac{{\sqrt 3 - 1}}{{\left( {1 + \sqrt 3 } \right)\left( {\sqrt 3 - 1} \right)}} \)\(+ \dfrac{{\sqrt 5 - \sqrt 3 }}{{\left( {\sqrt 3 + \sqrt 5 } \right)\left( {\sqrt 5 - \sqrt 3 } \right)}} \)\(+ ....... + \dfrac{{\sqrt {2021} - \sqrt {2019} }}{{\left( {\sqrt {2019} + \sqrt {2021} } \right)\left( {\sqrt {2021} - \sqrt {2019} } \right)}}\)\( = \dfrac{{\sqrt 3 - 1}}{{3 - 1}} + \dfrac{{\sqrt 5 - \sqrt 3 }}{{5 - 3}} \)\(+ ....... + \dfrac{{\sqrt {2021} - \sqrt {2019} }}{{2021 - 2019}}\)\( = \dfrac{{\sqrt 3 - 1}}{2} + \dfrac{{\sqrt 5 - \sqrt 3 }}{2} \)\(+ ...... + \dfrac{{\sqrt {2021} - \sqrt {2019} }}{2}\)\( = \dfrac{{\sqrt 3 - 1 + \sqrt 5 - \sqrt 3 + ....... + \sqrt {2021} - \sqrt {2019} }}{2}\)\( = \dfrac{{\sqrt {2021} - 1}}{2}\)
Tính diện tích một tam giác vuông có chu vi \(72\,cm\), hiệu giữa đường trung tuyến và đường cao ứng với cạnh huyền bằng \(7\,cm.\)
-
A.
\(100\,c{m^2}\)
-
B.
\(44\,c{m^2}\)
-
C.
\(144\,c{m^2}\)
-
D.
\(24\,c{m^2}\)
Đáp án : C
Đặt \(AM = x\,\left( {x > 0} \right)\) rồi dựa vào hệ thức lượng trong tam giác vuông để tìm ra phương trình ẩn \(x.\)
Giải phương trình ta tìm được \(x.\) Từ đó tính \(AH,BC \Rightarrow {S_{ABC}}.\)
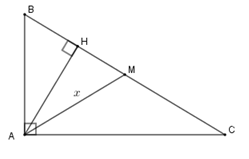
Đặt \(AM = x\,\left( {x > 0;cm} \right) \Rightarrow BC = 2x\,\left( {cm} \right);AH = x - 7\,\left( {cm} \right)\)
Vì chu vi tam giác \(ABC\) là \(72cm\) nên \(AB + AC + BC = 72 \Rightarrow AB + AC = 72 - 2x\,\left( {cm} \right)\)
Theo các hệ thức trong tam giác vuông:
\(A{B^2} + A{C^2} = B{C^2} = 4{x^2}\,\,\left( 1 \right)\) ; \(AB.AC = BC.AH = 2x\left( {x - 7} \right)\,\,\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(A{B^2} + A{C^2} + 2AB.AC = 4{x^2} + 4x\left( {x - 7} \right)\)
\( \Leftrightarrow {\left( {AB + AC} \right)^2} = 8{x^2} - 28x \Leftrightarrow {\left( {72 - 2x} \right)^2} = 8{x^2} - 28x\)
Đưa về phương trình \({x^2} + 65x - 1296 = 0 \Leftrightarrow \left( {x - 16} \right)\left( {x + 81} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 16\,\,\left( N \right)\\x = - 81\,\,\left( L \right)\end{array} \right.\)
Từ đó \(BC = 32\,cm;\,AH = 9\,cm.\) Khi đó \({S_{ABC}} = \dfrac{1}{2}.32.9 = 144\,\,\left( {c{m^2}} \right)\)
Cho đoạn thẳng $AB = 2a$ và trung điểm $O$ của nó. Trên nửa mặt phẳng bờ $AB$ vẽ các tia $Ax,By\;$ vuông góc với $AB.$ Qua \(O\) vẽ một tia cắt tia \(Ax\) tại $M$ sao cho $\widehat {AOM} = \alpha < {90^0}$ . Qua $O$ vẽ tia thứ hai cắt tia $By$ tại $N$ sao cho \(\widehat {MON} = 90^\circ \) . Khi đó, diện tích tam giác \(MON\) là
-
A.
\(\dfrac{{{a^2}}}{{2\sin \alpha .\cos \alpha }}\)
-
B.
\(\dfrac{{{a^2}}}{{\sin \alpha .\cos \alpha }}\)
-
C.
\(\dfrac{a}{{2\sin \alpha .\cos \alpha }}\)
-
D.
\(\dfrac{{2{a^2}}}{{\sin \alpha .\cos \alpha }}\)
Đáp án : A
Áp dụng hệ thức về cạnh và góc trong tam giác vuông
Áp dụng công thức tính diện tích tam giác vuông
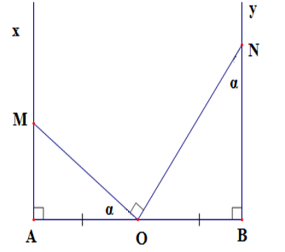
Theo đề bài ta có: \(AB = 2a \Rightarrow OA = OB = a\)
Ta có: \(\widehat {ONB} = \widehat {AOM} = \alpha \) (cùng phụ với \(\widehat {BON}\) )
Xét \(\Delta AOM\) có \(\widehat A = 90^\circ \) Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
\(OA = OM.\cos \alpha \Rightarrow OM = \dfrac{a}{{\cos \alpha }}\) Xét \(\Delta BON\) có \(\widehat B = 90^\circ \) Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
\(OB = ON.\sin \alpha \Rightarrow ON = \dfrac{a}{{\sin \alpha }}\) Vậy diện tích tam giác \(MON\) là: \(\dfrac{1}{2}OM.ON = \dfrac{1}{2}.\dfrac{a}{{\cos \alpha }}.\dfrac{a}{{\sin \alpha }} = \dfrac{{{a^2}}}{{2\sin \alpha .\cos \alpha }}\)
Tìm giá trị nhỏ nhất của biểu thức \(A = \dfrac{{x + \sqrt x + 4}}{{\sqrt x }}\) với \(x > 0\)
-
A.
\(5\)
-
B.
\(9\)
-
C.
\(4\)
-
D.
\(0\)
Đáp án : A
- Chia tử thức cho mẫu thức được \(A = \sqrt x + \dfrac{4}{{\sqrt x }} + 1\)
- Áp dụng bất đẳng thức Cô-si cho hai số dương \(\sqrt x \) và \(\dfrac{4}{{\sqrt x }}\)
Với \(x > 0\) ta có: \(A = \dfrac{{x + \sqrt x + 4}}{{\sqrt x }}\)\( = \dfrac{x}{{\sqrt x }} + \dfrac{{\sqrt x }}{{\sqrt x }} + \dfrac{4}{{\sqrt x }}\)\( = \sqrt x + \dfrac{4}{{\sqrt x }} + 1\)
Áp dụng bất đẳng thức Cô-si cho hai số dương \(\sqrt x \) và \(\dfrac{4}{{\sqrt x }}\) ta được:
\(\sqrt x + \dfrac{4}{{\sqrt x }} \ge 2\sqrt {\sqrt x .\dfrac{4}{{\sqrt x }}} = 2.2 = 4\)\( \Rightarrow \sqrt x + \dfrac{4}{{\sqrt x }} + 1 \ge 5\)
Dấu “=” xảy ra khi \(\sqrt x = \dfrac{4}{{\sqrt x }} \Leftrightarrow x = 4\,\,\,\left( {tm} \right)\)
Vậy GTNN của \(A\) là \(5\) khi \(x = 4\)