Đề kiểm tra 45 phút chương 8: Hình trụ-Hình nón-Hình cầu - Đề số 1
Đề bài
Cho hình cầu có đường kính \(d = 6\,cm\) . Diện tích mặt cầu là
-
A.
\(36\pi \,\left( {c{m^2}} \right)\)
-
B.
\(9\pi \,\left( {c{m^2}} \right)\)
-
C.
\(12\pi \,\left( {c{m^2}} \right)\)
-
D.
\(36\pi \,\left( {cm} \right)\)
Cho hình nón có chiều cao \(h = 10\,cm\) và thể tích \(V = 1000\pi \,\left( {c{m^3}} \right)\) . Tính diện tích toàn phần của hình nón
-
A.
\(100\pi \,\left( {c{m^2}} \right)\)
-
B.
\((300+200\sqrt3)\pi \,\left( {c{m^2}} \right)\)
-
C.
\(300\pi \,\left( {c{m^2}} \right)\)
-
D.
\(250\pi \,\left( {c{m^2}} \right)\)
Cho hình thang vuông $ABDC$ vuông tại $A$ và $B$ , biết cạnh $AB = BC = 3m,AD = 5cm$. Tính diện tích xung quanh hình nón cụt tạo thành khi quay hình thang quanh cạnh $AB$ .
-
A.
$7\pi \,\,\left( {c{m^2}} \right)$
-
B.
$7\pi \sqrt {10} \,\,\left( {c{m^2}} \right)$
-
C.
$7\sqrt {10} \,\,\left( {c{m^2}} \right)$
-
D.
$\pi \sqrt {10} \,\,\left( {c{m^2}} \right)$
Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao \(h = 12cm\) và đường kính đáy là \(d= 8\,cm\) . Tính diện tích các mặt của hộp sữa. Lấy \(\pi \approx 3,14\)
-
A.
\(110\pi \,\left( {c{m^2}} \right)\)
-
B.
\(128\pi \,\left( {c{m^2}} \right)\)
-
C.
\(96\pi \,\left( {c{m^2}} \right)\)
-
D.
\(112\pi \,\left( {c{m^2}} \right)\)
Cho hình trụ có bán kính đáy \(R = 4\,\left( {cm} \right)\) và chiều cao \(h = 5\,\left( {cm} \right)\) . Diện tích xung quanh của hình trụ là
-
A.
\(40\pi \)
-
B.
\(30\pi \)
-
C.
\(20\pi \)
-
D.
\(50\pi \)
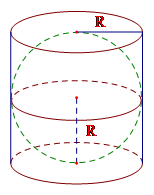
Cho một hình cầu nội tiếp trong hình trụ. Biết rằng đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính của hình cầu. Tính tỉ số giữa t hể tích hình cầu và thể tích hình trụ.
-
A.
\(\dfrac{2}{3}\)
-
B.
\(\dfrac{3}{2}\)
-
C.
\(\dfrac{1}{2}\)
-
D.
\(2\)
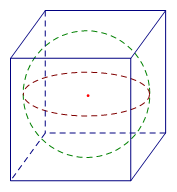
Cho một hình cầu và một hình lập phương ngoại tiếp nó. Tính tỉ số giữa d iện tích mặt cầu và diện tích toàn phần của hình lập phương .
-
A.
\(\dfrac{6}{\pi }\)
-
B.
\(\dfrac{1}{6}\)
-
C.
\(\dfrac{\pi }{6}\)
-
D.
\(\dfrac{1}{3}\)
Tính diện tích xung quanh của một hình trụ có bán kính đáy là $4\,cm$ và chiều cao là \(6\,cm\) .
-
A.
\(48\pi \,\left( {c{m^2}} \right)\)
-
B.
$96\left( {c{m^2}} \right)$
-
C.
\(192\,\left( {c{m^2}} \right)\)
-
D.
\(48 \,\left( {c{m^2}} \right)\)
Nếu ta tăng bán kính đáy và chiều cao của một hình nón lên hai lần thì diện tích xung quanh của hình nón đó
-
A.
Tăng \(4\) lần
-
B.
Giảm \(4\) lần
-
C.
Tăng \(2\) lần
-
D.
Không đổi
Cho mặt cầu có thể tích \(V = 288\pi \,\left( {c{m^3}} \right)\) . Tính đường kính mặt cầu.
-
A.
\(6\,cm\)
-
B.
\(12\,cm\)
-
C.
\(8\,cm\)
-
D.
\(16\,cm\)
Một hình trụ có thể tích \(V\) không đổi. Hỏi bán kính đáy bằng bao nhiêu để diện tích toàn phần của hình trụ đó là nhỏ nhất.
-
A.
\(R = \sqrt[3]{{\dfrac{V}{{2\pi }}}}\)
-
B.
\(R = \sqrt {\dfrac{V}{{2\pi }}} \)
-
C.
\(R = \dfrac{{\sqrt[3]{V}}}{{2\pi }}\)
-
D.
\(R = 3\sqrt[3]{{\dfrac{V}{{2\pi }}}}\)
Cho tam giác \(ABC\) đều cạnh \(a\) , đường trung tuyến \(AM\) . Quay tam giác \(ABC\) quanh cạnh \(AM\) . Tính diện tích toàn phần của hình nón tạo thành.
-
A.
\(\dfrac{{3\pi {a^2}}}{2}\)
-
B.
\(\dfrac{{3\pi {a^2}}}{4}\)
-
C.
\(\dfrac{{5\pi {a^2}}}{2}\)
-
D.
\(\dfrac{{\pi {a^2}}}{2}\)
Cho hình chữ nhật \(ABCD\) có \(AB = 4\,cm;AD = 3\,cm\) . Tính diện tích mặt cầu thu được khi quay nửa đường tròn ngoại tiếp hình chữ nhật \(ABCD\) quanh đường thẳng \(MN\) với \(M\) là trung điểm \(AD\) , \(N\) là trung điểm \(BC\) .
-
A.
\(25\pi \)
-
B.
\(\dfrac{{25\pi }}{8}\)
-
C.
\(25\)
-
D.
\(\dfrac{{25\pi }}{4}\)
Một hình nón có diện tích xung quanh bằng $960\;c{m^2}$ , chu vi đáy bằng $48\,\left( {cm} \right).$ Đường sinh của hình nón đó bằng
-
A.
\(4\pi \,cm\)
-
B.
\(20\,cm\)
-
C.
\(40\pi \,cm\)
-
D.
\(40\,cm\)
Cho một hình trụ, một hình nón và một hình cầu có thể tích bằng nhau. Bán kính đáy của hình trụ, bán kính đáy của hình nón và bán kính của hình cầu đều bằng $R.$ Tính các chiều cao \({h_1}\) của hình trụ và \({h_2}\) của hình nón theo \(R.\)
-
A.
\({h_1} = 4R;{h_2} = \dfrac{4}{3}R\)
-
B.
\({h_1} = \dfrac{4}{3}R;{h_2} = 4R\)
-
C.
\({h_1} = \dfrac{1}{3}R;{h_2} = 4R\)
-
D.
\({h_1} = \dfrac{4}{3}R;{h_2} = \dfrac{1}{3}R\)
Lời giải và đáp án
Cho hình cầu có đường kính \(d = 6\,cm\) . Diện tích mặt cầu là
-
A.
\(36\pi \,\left( {c{m^2}} \right)\)
-
B.
\(9\pi \,\left( {c{m^2}} \right)\)
-
C.
\(12\pi \,\left( {c{m^2}} \right)\)
-
D.
\(36\pi \,\left( {cm} \right)\)
Đáp án : A
Sử dụng công thức diện tích mặt cầu $S = 4\pi {R^2}$
Vì đường kính \(d = 6\,cm\) nên bán kính hình cầu \(R = \dfrac{6}{2} = 3\,\,cm\)
Diện tích mặt cầu $S = 4\pi {R^2} = 4\pi {.3^2} = 36\pi \,\,\left( {c{m^2}} \right)$
Cho hình nón có chiều cao \(h = 10\,cm\) và thể tích \(V = 1000\pi \,\left( {c{m^3}} \right)\) . Tính diện tích toàn phần của hình nón
-
A.
\(100\pi \,\left( {c{m^2}} \right)\)
-
B.
\((300+200\sqrt3)\pi \,\left( {c{m^2}} \right)\)
-
C.
\(300\pi \,\left( {c{m^2}} \right)\)
-
D.
\(250\pi \,\left( {c{m^2}} \right)\)
Đáp án : B
Sử dụng công thức thể tich khối nón \(V = \dfrac{1}{3}\pi {R^2}h\) để tính bán kính đường tròn đáy
Sử dụng công thức liên hệ\({R^2} + {h^2} = {l^2}\) để tìm đường sinh của hình nón
Sử dụng công thức tính diện tích toàn phần của hình nón \({S_{tp}} = \pi Rl + \pi {R^2}\)
Ta có \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {R^2}.10 = 1000\pi \)
nên \({R^2} = 300\) suy ra \( R = 10\sqrt 3 \)
Và \({R^2} + {h^2} = {l^2}\) hay \( {10^2} + {\left( {10\sqrt 3 } \right)^2} = {l^2} \) suy ra \( l = 20\,cm\)
Diện tích toàn phần của hình nón là:
\({S_{tp}} = \pi Rl + \pi {R^2} = \pi .10\sqrt3.20 + \pi.300= (300+200\sqrt3)\pi \,\left( {c{m^2}} \right)\)
Cho hình thang vuông $ABDC$ vuông tại $A$ và $B$ , biết cạnh $AB = BC = 3m,AD = 5cm$. Tính diện tích xung quanh hình nón cụt tạo thành khi quay hình thang quanh cạnh $AB$ .
-
A.
$7\pi \,\,\left( {c{m^2}} \right)$
-
B.
$7\pi \sqrt {10} \,\,\left( {c{m^2}} \right)$
-
C.
$7\sqrt {10} \,\,\left( {c{m^2}} \right)$
-
D.
$\pi \sqrt {10} \,\,\left( {c{m^2}} \right)$
Đáp án : B
Tính đáy \(BD\)và \(CD\) theo định lý Pytago
Sử dụng công thức diện tích xung quanh hình nón cụt ${S_{xq}} = \pi (R + r)l.$
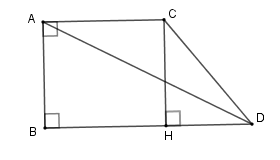
Xét tam giác vuông \(ABD\) ta có \(BD = \sqrt {A{D^2} - A{B^2}} = \sqrt {{5^2} - {3^2}} = 4\,\,\left( {cm} \right)\)
Kẻ $CH \bot BD$ tại \(H\) . Khi đó \(ACHB\) là hình vuông nên\(CH = AB = AC = BH = 3\,cm \Rightarrow HD = 4 - 3 = 1\,cm\)
Xét tam giác vuông \(CHD\) ta có \(C{D^2} = C{H^2} + H{D^2} = {3^2} + {1^2}=10\Rightarrow CD = \sqrt {10} \)
Khi quay hình thang vuông \(ABDC\) quanh cạnh \(AB\) ta được hình nón cụt có bán kính đáy nhỏ \(AC\) , bán kính đáy lớn \(BD\) , đường sinh \(CD\) và chiều cao \(AB\) .
Khi đó diện tích xung quanh hình nón cụt là ${S_{xq}} = \pi (R + r)l = \pi \left( {3 + 4} \right)\sqrt {10} = 7\pi \sqrt {10} \,\,\left( {c{m^2}} \right)$
Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao \(h = 12cm\) và đường kính đáy là \(d= 8\,cm\) . Tính diện tích các mặt của hộp sữa. Lấy \(\pi \approx 3,14\)
-
A.
\(110\pi \,\left( {c{m^2}} \right)\)
-
B.
\(128\pi \,\left( {c{m^2}} \right)\)
-
C.
\(96\pi \,\left( {c{m^2}} \right)\)
-
D.
\(112\pi \,\left( {c{m^2}} \right)\)
Đáp án : D
Sử dụng công thức tính diện tích xung quanh của hình trụ ${S_{xq}} = 2\pi Rh$ và diện tích một đáy ${S_d} = \pi {R^2}.$
Bán kính đường tròn đáy \(R = \dfrac{8}{2} = 4\,cm\) nên diện tích một đáy ${S_d} = \pi {R^2} = 16\pi \,(c{m^2})$
Ta có diện tích xung quanh của hình trụ: ${S_{xq}} = 2\pi Rh = 2\pi .4.12 = 96\pi \,(c{m^2})$
Vì hộp sữa đã mất nắp nên diện tích các mặt của hộp sữa là:
\(96\pi + 16\pi = 112\pi \,\left( {c{m^2}} \right).\)
Cho hình trụ có bán kính đáy \(R = 4\,\left( {cm} \right)\) và chiều cao \(h = 5\,\left( {cm} \right)\) . Diện tích xung quanh của hình trụ là
-
A.
\(40\pi \)
-
B.
\(30\pi \)
-
C.
\(20\pi \)
-
D.
\(50\pi \)
Đáp án : A
Sử dụng công thức tính diện tích xung quanh của hình trụ bán kính \(R\) và chiều cao \(h\)
\({S_{xq}} = 2\pi Rh\)
Diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi Rh = 2\pi .4.5 = 40\pi \,\,\left( {c{m^2}} \right)\)
Cho một hình cầu nội tiếp trong hình trụ. Biết rằng đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính của hình cầu. Tính tỉ số giữa t hể tích hình cầu và thể tích hình trụ.

-
A.
\(\dfrac{2}{3}\)
-
B.
\(\dfrac{3}{2}\)
-
C.
\(\dfrac{1}{2}\)
-
D.
\(2\)
Đáp án : A
Sử dụng công thức thể tích hình cầu $V = \dfrac{4}{3}\pi {R^3}$ và thể tích của khối trụ \(V = \pi {R^2}h\)
Vì đường kính đáy và chiều cao của hình trụ bằng nhau và bằng đường kính hình cầu nên \(h = 2R\) với \(R\) là bán kính hình cầu và cũng là bán kính đáy của hình trụ.
Thể tích hình cầu \({V_{cầu}} = \dfrac{4}{3}\pi {R^3}\) ; thể tích khối trụ ${V_{trụ}} = \pi {R^2}.2R = 2\pi {R^3}$
Tỉ số thể tích hình cầu và thể tích hình trụ là \(\dfrac{{{V_{cầu}}}}{{{V_{trụ}}}} = \dfrac{{\dfrac{4}{3}\pi {R^3}}}{{2\pi {R^3}}} = \dfrac{2}{3}\) .
Cho một hình cầu và một hình lập phương ngoại tiếp nó. Tính tỉ số giữa d iện tích mặt cầu và diện tích toàn phần của hình lập phương .

-
A.
\(\dfrac{6}{\pi }\)
-
B.
\(\dfrac{1}{6}\)
-
C.
\(\dfrac{\pi }{6}\)
-
D.
\(\dfrac{1}{3}\)
Đáp án : C
Sử dụng công thức diện tích mặt cầu $S = 4\pi {R^2}$ và diện tích toàn phần của hình lập phương \({S_{tp}} = 6{a^2}\) với \(a\) là độ dài cạnh của hình lập phương.
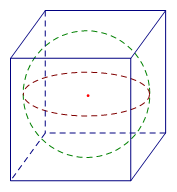
Vì hình cầu nội tiếp hình lập phương nên bán kính hình cầu \(R = \dfrac{a}{2}\) với \(a\) là cạnh hình lập phương.
Khi đó ta có diện tích mặt cầu là:
\(S = 4\pi {R^2} = 4\pi .{\left( {\dfrac{a}{2}} \right)^2} = \pi {a^2}\)
Diện tích toàn phần của hình lập phương là:
\({S_{tp}} = 6{a^2}\)
Tỉ số giữa d iện tích mặt cậu và diện tích toàn phần của hình lập phương là:
\(\dfrac{S}{{{S_{tp}}}} = \dfrac{{\pi {a^2}}}{{6{a^2}}} = \dfrac{\pi }{6}\)
Tính diện tích xung quanh của một hình trụ có bán kính đáy là $4\,cm$ và chiều cao là \(6\,cm\) .
-
A.
\(48\pi \,\left( {c{m^2}} \right)\)
-
B.
$96\left( {c{m^2}} \right)$
-
C.
\(192\,\left( {c{m^2}} \right)\)
-
D.
\(48 \,\left( {c{m^2}} \right)\)
Đáp án : A
Sử dụng công thức tính diện tích xung quanh hình trụ có bán kính đáy $R$ và chiều cao \(h\) là \({S_{xq}} = 2\pi {R}h\)
Diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi {.4}.6 = 48\pi \,\left( {c{m^2}} \right).\)
Nếu ta tăng bán kính đáy và chiều cao của một hình nón lên hai lần thì diện tích xung quanh của hình nón đó
-
A.
Tăng \(4\) lần
-
B.
Giảm \(4\) lần
-
C.
Tăng \(2\) lần
-
D.
Không đổi
Đáp án : A
Sử dụng công thức liên hệ \({R^2} + {h^2} = {l^2}\)
Sử dụng công thức tính diện tích xung quanh của hình nón \({S_{xq}} = \pi Rl\) .
Ta có đường sinh mới là: \({l'^2} = {\left( {2R} \right)^2} + {\left( {2h} \right)^2} = 4\left( {{R^2} + {h^2}} \right) = {\left( {2l} \right)^2} \)
Suy ra \(l' = 2l\)
Khi đó diện tích xung quanh mới là:
\({S'_{xq}} = \pi .\left( {2R} \right).\left( {2l} \right) = 4.\pi Rl = 4{S_{xq}}\) .
Vậy diện tích xung quanh của hình nón tăng \(4\) lần.
Cho mặt cầu có thể tích \(V = 288\pi \,\left( {c{m^3}} \right)\) . Tính đường kính mặt cầu.
-
A.
\(6\,cm\)
-
B.
\(12\,cm\)
-
C.
\(8\,cm\)
-
D.
\(16\,cm\)
Đáp án : B
Sử dụng công thức thể tích khối cầu $V = \dfrac{4}{3}\pi {R^3}$ để tính bán kính, từ đó suy ra đường kính của mặt cầu.
Ta có:
\(V = \dfrac{4}{3}\pi {R^3} = 288\pi \)
\({R^3} = 216\)
\(R = 6\,cm\)
Từ đó đường kính mặt cầu là \(d = 2R = 2.6 = 12\,cm\).
Một hình trụ có thể tích \(V\) không đổi. Hỏi bán kính đáy bằng bao nhiêu để diện tích toàn phần của hình trụ đó là nhỏ nhất.
-
A.
\(R = \sqrt[3]{{\dfrac{V}{{2\pi }}}}\)
-
B.
\(R = \sqrt {\dfrac{V}{{2\pi }}} \)
-
C.
\(R = \dfrac{{\sqrt[3]{V}}}{{2\pi }}\)
-
D.
\(R = 3\sqrt[3]{{\dfrac{V}{{2\pi }}}}\)
Đáp án : A
Sử dụng công thức diện thể tích của hình trụ $V = \pi {R^2}h$ và công thức diện tích toàn phần \({S_{tp}} = 2\pi Rh + 2\pi {R^2}\)
Sử dụng bất đẳng thức Cô-si cho ba số dương \(a,b,\,c\) là \(a + b + c \ge 3\sqrt[3]{{abc}}\)
Dấu “=” xảy ra khi \(a = b = c\)
Gọi bán kính đáy và chiều cao của hình trụ lần lượt là \(R,\,\,h\,\,\left( {R > 0;\,h > 0} \right)\)
Ta có \(V = \pi {R^2}h\) suy ra \(h = \dfrac{V}{{\pi {R^2}}}\)
Diện tích toàn phần của hình trụ là:
\({S_{tp}} = 2\pi Rh + 2\pi {R^2} = 2\pi R.\dfrac{V}{{\pi {R^2}}} + 2\pi {R^2} = \dfrac{{2V}}{R} + 2\pi {R^2}\)
\( = \dfrac{V}{R} + \dfrac{V}{R} + 2\pi {R^2} \ge 3\sqrt[3]{{\dfrac{V}{R}.\dfrac{V}{R}.2\pi {R^2}}} = 3\sqrt[3]{{2\pi {V^2}}}\) (theo bất đẳng thức Cosi)
Dấu “=” xảy ra khi \(\dfrac{V}{R} = 2\pi {R^2}\) suy ra \(R = \sqrt[3]{{\dfrac{V}{{2\pi }}}}\)
Vậy với \(R = \sqrt[3]{{\dfrac{V}{{2\pi }}}}\) thì \({S_{tp}}\) đạt giá trị nhỏ nhất là \(3\sqrt[3]{{2\pi {V^2}}}\).
Cho tam giác \(ABC\) đều cạnh \(a\) , đường trung tuyến \(AM\) . Quay tam giác \(ABC\) quanh cạnh \(AM\) . Tính diện tích toàn phần của hình nón tạo thành.
-
A.
\(\dfrac{{3\pi {a^2}}}{2}\)
-
B.
\(\dfrac{{3\pi {a^2}}}{4}\)
-
C.
\(\dfrac{{5\pi {a^2}}}{2}\)
-
D.
\(\dfrac{{\pi {a^2}}}{2}\)
Đáp án : B
Sử dụng công thức tính diện tích toàn phần của hình nón \({S_{tp}} = \pi Rl + \pi {R^2}\) .
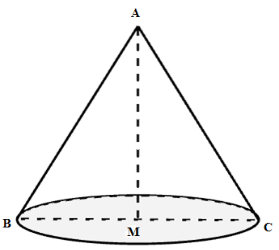
Xét tam giác \(ABC\) đều có \(AM\) vừa là đường trung tuyến, đường cao, đường phân giác.
Nên ta có \(MC = \dfrac{{BC}}{2} = \dfrac{a}{2}\) .
Khi quay tam giác $ABC$ quanh cạnh \(AM\) ta được hình nón đỉnh \(A\) , bán kính đáy là \(MC\) , đường sinh \(AC\) và chiều cao \(AM\) .
Diện tích toàn phần của hình nón là \({S_{tp}} = \pi Rl + \pi {R^2} = \pi .MC.AC + \pi .M{C^2} = \pi .\dfrac{a}{2}.a + \pi .{\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{3\pi {a^2}}}{4}\) .
Cho hình chữ nhật \(ABCD\) có \(AB = 4\,cm;AD = 3\,cm\) . Tính diện tích mặt cầu thu được khi quay nửa đường tròn ngoại tiếp hình chữ nhật \(ABCD\) quanh đường thẳng \(MN\) với \(M\) là trung điểm \(AD\) , \(N\) là trung điểm \(BC\) .
-
A.
\(25\pi \)
-
B.
\(\dfrac{{25\pi }}{8}\)
-
C.
\(25\)
-
D.
\(\dfrac{{25\pi }}{4}\)
Đáp án : A
Công thức diện tích mặt cầu $S = 4\pi {R^2}$
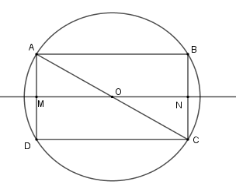
Gọi \(O\) là tâm của hình chữ nhật nên $OA = OB = OC = OD$ nên \(O\) là tâm đường tròn ngoại tiếp hình chữ nhật \(ABCD\) . Khi đó bán kính đường tròn là \(R = OA = \dfrac{{AC}}{2}\)
Áp dụng định lí Pythagore vào tam giác ADC, ta có:
\(A{C^2} = A{D^2} + D{C^2} = {3^2} + {4^2} = 25\)
suy ra \(AC = 5\) (vì \(AB = DC = 4\,cm\) )
Do đó \( R = \dfrac{5}{2}\)
Khi quay nửa đường tròn ngoại tiếp hình chữ nhật \(ABCD\) quay quanh đường thẳng \(MN\) với \(M\) là trung điểm \(AD\) , \(N\) là trung điểm \(BC\) ta được một hình cầu tâm \(O\) bán kính $R = \dfrac{5}{2}$
Diện tích mặt cầu là:
\(S = 4\pi {R^2} = 4.\pi {\left( {\dfrac{5}{2}} \right)^2} = 25\pi \) \(\left( {cm} \right)\) .
Một hình nón có diện tích xung quanh bằng $960\;c{m^2}$ , chu vi đáy bằng $48\,\left( {cm} \right).$ Đường sinh của hình nón đó bằng
-
A.
\(4\pi \,cm\)
-
B.
\(20\,cm\)
-
C.
\(40\pi \,cm\)
-
D.
\(40\,cm\)
Đáp án : D
Sử dụng công thức tính chu vi đường tròn đáy \(C = 2\pi R\) và công thức tính diện tích xung quanh hình nón \({S_{xq}} = \pi Rl\) với \(R\) là bán kính đáy, \(l\) là đường sinh của hình nón.
Gọi \(R\) là bán kính đáy và \(l\) là đường sinh của hình nón.
Vì chu vi đáy là $48\left( {cm} \right) \Rightarrow 2\pi R = 48\, \Rightarrow R = \dfrac{{24}}{\pi }\,cm.$
Diện tích xung quanh \({S_{xq}} = \pi Rl \Leftrightarrow \pi .\dfrac{{24}}{\pi }.l = 960 \Rightarrow l = 40\,cm\)
Cho một hình trụ, một hình nón và một hình cầu có thể tích bằng nhau. Bán kính đáy của hình trụ, bán kính đáy của hình nón và bán kính của hình cầu đều bằng $R.$ Tính các chiều cao \({h_1}\) của hình trụ và \({h_2}\) của hình nón theo \(R.\)
-
A.
\({h_1} = 4R;{h_2} = \dfrac{4}{3}R\)
-
B.
\({h_1} = \dfrac{4}{3}R;{h_2} = 4R\)
-
C.
\({h_1} = \dfrac{1}{3}R;{h_2} = 4R\)
-
D.
\({h_1} = \dfrac{4}{3}R;{h_2} = \dfrac{1}{3}R\)
Đáp án : B
Sử dụng công thức
+ Thể tích hình trụ : $V = \pi {R^2}{h_1}$.
+ Thể tích hình nón : $V = \dfrac{1}{3}\pi {R^2}{h_2}.$
+ Thể tích hình cầu : \(V = \dfrac{4}{3}\pi {R^3}\)
Cho ba thể tích trên bằng nhau rồi giải hệ để tìm ${h_1};{h_2}$
+ Thể tích hình trụ : ${V_1} = \pi {R^2}{h_1}$.
+ Thể tích hình nón : ${V_2} = \dfrac{1}{3}\pi {R^2}{h_2}.$
+ Thể tích hình cầu : \({V_3} = \dfrac{4}{3}\pi {R^3}\)
Ta có ${V_1} = {V_2} = {V_3}$
Nên \(\left\{ \begin{array}{l}\pi {R^2}{h_1} = \dfrac{4}{3}\pi {R^3}\\\dfrac{1}{3}\pi {R^2}{h_2} = \dfrac{4}{3}\pi {R^3}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{h_1} = \dfrac{4}{3}R\\{h_2} = 4R\end{array} \right.\)