Đề kiểm tra 45 phút chương 6: Đường tròn - Đề số 1
Đề bài
Nếu đường thẳng và đường tròn có hai điểm chung thì
-
A.
đường thẳng tiếp xúc với đường tròn
-
B.
đường thẳng cắt đường tròn
-
C.
đường thẳng không cắt đường tròn
-
D.
đáp án khác.
Tâm đối xứng của đường tròn là:
-
A.
Điểm bất kì bên trong đường tròn
-
B.
Điểm bất kì bên ngoài đường tròn
-
C.
Điểm bất kì trên đường tròn
-
D.
Tâm của đường tròn
Cho tam giác $ABC$ có $AC = 3cm,AB = 4cm,BC = 5cm$. Vẽ đường tròn $\left( {C;CA} \right)$. Khẳng định nào sau đây là đúng?
-
A.
Đường thẳng $BC$ cắt đường tròn $\left( {C;CA} \right)$ tại một điểm
-
B.
$AB$ là cát tuyến của đường tròn $\left( {C;CA} \right)$
-
C.
$AB$ là tiếp tuyến của $\left( {C;CA} \right)$
-
D.
$BC$ là tiếp tuyến của $\left( {C;CA} \right)$
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ không đi qua tâm. Biết rằng khoảng cách từ tâm đến hai dây là bằng nhau. Kết luận nào sau đây là đúng ?
-
A.
$AB > CD$
-
B.
$AB = CD$
-
C.
$AB < CD$
-
D.
$AB{\rm{//}}CD$
“Nếu một đường thẳng đi qua một điểm của đường tròn và … thì đường thẳng ấy là một tiếp tuyến của đường tròn”. Cụm từ thích hợp điền vào chỗ trống là
-
A.
song song với bán kính đi qua điểm đó
-
B.
vuông góc với bán kính đi qua điểm đó
-
C.
song song với bán kính đường tròn
-
D.
vuông góc với bán kính bất kì
Cho tam giác $ABC$ có các đường cao $BD,CE$ . Biết rằng bốn điểm $B,E,D,C$ cùng nằm trên một đường tròn. Chỉ rõ tâm và bán kính của đường tròn đó.
-
A.
Tâm là trọng tâm tam giác $ABC$ và bán kính $R = \dfrac{2}{3}AI$ với $I$ là trung điểm của $BC$.
-
B.
Tâm là trung điểm $AB$ và bán kính là $R = \dfrac{{AB}}{2}$
-
C.
Tâm là giao điểm của $BD$ và $EC$ , bán kính là $R = \dfrac{{BD}}{2}$
-
D.
Tâm là trung điểm $BC$ và bán kính là $R = \dfrac{{BC}}{2}$
Cho tam giác \(ABC\) vuông tại \(A\) , có\(AB = 5cm;AC = 12cm\) . Tính bán kính đường tròn ngoại tiếp tam giác \(ABC\) .
-
A.
\(R = 26\)
-
B.
\(R = 13\)
-
C.
\(R = \dfrac{{13}}{2}\)
-
D.
\(R = 6\)
Cho đường tròn \(\left( {O;R} \right)\) có hai dây \(AB,CD\) vuông góc với nhau ở \(M\). Biết\(\,CD = 8\,cm;\,MC = 1\,cm\). Khoảng cách từ tâm \(O\) đến dây \(AB\) là
-
A.
\(4\,cm\)
-
B.
\(5\,cm\)
-
C.
\(3\,cm\)
-
D.
\(2\,cm\)
Cho các đường tròn \(\left( {A;10\,{\rm{cm}}} \right),{\rm{ }}\left( {B;15\,{\rm{cm}}} \right),{\rm{ }}\left( {C;15\,cm} \right)\) tiếp xúc ngoài với nhau đôi một. Hai đường tròn (B) và (C) tiếp xúc với nhau tại \(A'\). Đường tròn \(\left( A \right)\) tiếp xúc với đường tròn \(\left( B \right)\) và \(\left( C \right)\) lần lượt tại \(C'\) và \(B'.\)
Chọn câu đúng nhất.
-
A.
\(AA'\) là tiếp tuyến chung của đường tròn \(\left( B \right)\) và \(\left( C \right).\)
-
B.
\(AA' = 25\,cm\)
-
C.
\(AA' = 15\,cm\)
-
D.
Cả A và B đều đúng
Tính diện tích tam giác \(A'B'C'.\)
-
A.
\(36\,c{m^2}\)
-
B.
\(72\,c{m^2}\)
-
C.
\(144\,c{m^2}\)
-
D.
\(96\,c{m^2}\)
Cho hình vuông \(ABCD.\) Gọi \(M,N\) lần lượt là trung điểm của \(AB,BC\) . Gọi \(E\) là giao điểm của \(CM\) và \(DN\) . So sánh \(AE\) và \(DM.\)
-
A.
\(AM = \dfrac{3}{2}AE\)
-
B.
\(DM < AE\)
-
C.
\(DM = AE\)
-
D.
\(DM > AE\)
Cho tam giác $ABC$ cân tại $A$; đường cao $AH$ và $BK$ cắt nhau tại $I$. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính $AI$.
-
A.
$HK$
-
B.
$IB$
-
C.
$IC$
-
D.
$AC$
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Đường tròn đường kính $BH$ cắt $AB$ tại $D$, đường tròn đường kính $CH$ cắt $AC$ tại $E$ . Chọn khẳng định sai trong các khẳng định sau
-
A.
$DE$ là cát tuyến của đường tròn đường kính $BH$
-
B.
$DE$ là tiếp tuyến của đường tròn đường kính $BH$
-
C.
Tứ giác$AEHD$ là hình chữ nhật
-
D.
$DE \bot DI$ (với $I$ là trung điểm $BH$)
Trên mặt phẳng tọa độ $Oxy$, cho điểm $A\left( {4;5} \right)$. Hãy xác định vị trí tương đối của đường tròn $\left( {A;5} \right)$ và các trục tọa độ.
-
A.
Trục tung cắt đường tròn và trục hoành tiếp xúc với đường tròn.
-
B.
Trục hoành cắt đường tròn và trục tung tiếp xúc với đường tròn
-
C.
Cả hai trục tọa độ đều cắt đường tròn
-
D.
Cả hai trục tọa độ đều tiếp xúc với đường tròn.
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai ?
-
A.
$AC = CB$
-
B.
$\widehat {CBO'} = 90^\circ $
-
C.
$CA,CB$ là hai tiếp tuyến của $\left( {O'} \right)$
-
D.
$CA,CB$ là hai cát tuyến của $\left( {O'} \right)$
Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\)tiếp xúc ngoài tại \(A\). Kẻ các đường kính \(AOB;AO'C\). Gọi \(DE\) là tiếp tuyến chung của hai đường tròn \(\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)\). Gọi \(M\) là giao điểm của \(BD\) và \(CE\). Tính diện tích tứ giác \(ADME\) biết \(\widehat {DOA} = 60^\circ \) và \(OA = 8\,cm\)
-
A.
\(12\sqrt 3 \,\,c{m^2}\)
-
B.
\( \dfrac{64}{3}\sqrt 3 \,\,c{m^2}\)
-
C.
\( \dfrac{32}{3}\sqrt 3 \,\,c{m^2}\)
-
D.
\(36\,\,c{m^2}\)
Cho đường tròn \(\left( {O;R} \right)\) và điểm A nằm ngoài \(\left( O \right)\). Từ A kẻ hai tiếp tuyến AB, AC với \(\left( O \right)\) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với \(\left( O \right)\) (E không trùng với D).
Chọn câu đúng nhất.
-
A.
Bốn điểm A, B, O, C cùng thuộc một đường tròn đường kính AC
-
B.
BC là đường trung trực của OA
-
C.
Cả A, B đều đúng.
-
D.
Cả A, B đều sai
Tỉ số \(\dfrac{{DE}}{{BE}}\) bằng
-
A.
\(\dfrac{{DA}}{{BA}}\)
-
B.
\(\dfrac{{BA}}{{DA}}\)
-
C.
\(\dfrac{{BD}}{{BA}}\)
-
D.
\(\dfrac{{BA}}{{BD}}\)
Số đo góc \(HEC\) là
-
A.
\(60^\circ \)
-
B.
\(80^\circ \)
-
C.
\(45^\circ \)
-
D.
\(90^\circ \)
Cho đường thẳng xy và đường tròn (O; R) không giao nhau. Gọi M là một điểm di động trên xy. Vẽ đường tròn đường kính OM cắt đường tròn (O) tại A và B. Kẻ \(OH \bot xy\) . Chọn câu đúng.
-
A.
Đường thẳng AB luôn đi qua một điểm cố định là \(H.\)
-
B.
Đường thẳng AB luôn đi qua một điểm cố định là trung điểm \(OH\) .
-
C.
Đường thẳng AB luôn đi qua một điểm cố định là giao của \(OH\) và \(AB.\)
-
D.
Đường thẳng AB luôn đi qua một điểm cố định là giao của \(OH\) và \(\left( {O;R} \right).\)
Lời giải và đáp án
Nếu đường thẳng và đường tròn có hai điểm chung thì
-
A.
đường thẳng tiếp xúc với đường tròn
-
B.
đường thẳng cắt đường tròn
-
C.
đường thẳng không cắt đường tròn
-
D.
đáp án khác.
Đáp án : B

Đường thẳng và đường tròn có hai điểm chung thì đường thẳng cắt đường tròn.
Tâm đối xứng của đường tròn là:
-
A.
Điểm bất kì bên trong đường tròn
-
B.
Điểm bất kì bên ngoài đường tròn
-
C.
Điểm bất kì trên đường tròn
-
D.
Tâm của đường tròn
Đáp án : D
Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.
Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn.
Cho tam giác $ABC$ có $AC = 3cm,AB = 4cm,BC = 5cm$. Vẽ đường tròn $\left( {C;CA} \right)$. Khẳng định nào sau đây là đúng?
-
A.
Đường thẳng $BC$ cắt đường tròn $\left( {C;CA} \right)$ tại một điểm
-
B.
$AB$ là cát tuyến của đường tròn $\left( {C;CA} \right)$
-
C.
$AB$ là tiếp tuyến của $\left( {C;CA} \right)$
-
D.
$BC$ là tiếp tuyến của $\left( {C;CA} \right)$
Đáp án : C
Sử dụng cách chứng minh tiếp tuyến
Để chứng minh đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm là $M$ ta chứng minh $OM \bot d$ tại $M$ và $M \in \left( O \right)$.
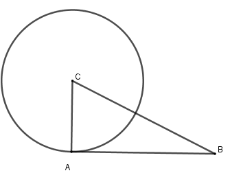
+) Xét tam giác $ABC$ có \(B{C^2} = {5^2} = 25;A{B^2} + A{C^2} = {4^2} + {3^2} = 25; \Rightarrow B{C^2} = A{B^2} + A{C^2}\)
\( \Rightarrow \Delta ABC\) vuông tại A (định lý Pytago đảo)
\( \Rightarrow AB \bot AC\) mà $A \in \left( {C;CA} \right)$ nên $AB$ là tiếp tuyến của $\left( {C;CA} \right)$
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ không đi qua tâm. Biết rằng khoảng cách từ tâm đến hai dây là bằng nhau. Kết luận nào sau đây là đúng ?
-
A.
$AB > CD$
-
B.
$AB = CD$
-
C.
$AB < CD$
-
D.
$AB{\rm{//}}CD$
Đáp án : B
- Trong một đường tròn: Hai dây cách đều tâm thì bằng nhau.
“Nếu một đường thẳng đi qua một điểm của đường tròn và … thì đường thẳng ấy là một tiếp tuyến của đường tròn”. Cụm từ thích hợp điền vào chỗ trống là
-
A.
song song với bán kính đi qua điểm đó
-
B.
vuông góc với bán kính đi qua điểm đó
-
C.
song song với bán kính đường tròn
-
D.
vuông góc với bán kính bất kì
Đáp án : B
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Cho tam giác $ABC$ có các đường cao $BD,CE$ . Biết rằng bốn điểm $B,E,D,C$ cùng nằm trên một đường tròn. Chỉ rõ tâm và bán kính của đường tròn đó.
-
A.
Tâm là trọng tâm tam giác $ABC$ và bán kính $R = \dfrac{2}{3}AI$ với $I$ là trung điểm của $BC$.
-
B.
Tâm là trung điểm $AB$ và bán kính là $R = \dfrac{{AB}}{2}$
-
C.
Tâm là giao điểm của $BD$ và $EC$ , bán kính là $R = \dfrac{{BD}}{2}$
-
D.
Tâm là trung điểm $BC$ và bán kính là $R = \dfrac{{BC}}{2}$
Đáp án : D
Sử dụng: Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
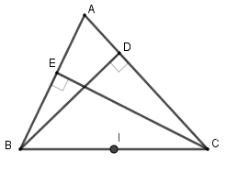
Gọi $I$ là trung điểm của $BC$.
Xét tam giác $BEC$ vuông tại $E$ có $EI = IB = IC = \dfrac{{BC}}{2}$ (vì $EI$ là đường trung tuyến ứng với cạnh huyền)
Xét tam giác $BDC$ vuông tại $D$ có $DI = IB = IC = \dfrac{{BC}}{2}$ (vì $DI$ là đường trung tuyến ứng với cạnh huyền)
Từ đó ta có $ID = IE = IB = IC = \dfrac{{BC}}{2}$ nên $I$ là tâm đường tròn ngoại tiếp tứ giác $DEBC$ và bán kính $R = \dfrac{{BC}}{2}$.
Cho tam giác \(ABC\) vuông tại \(A\) , có\(AB = 5cm;AC = 12cm\) . Tính bán kính đường tròn ngoại tiếp tam giác \(ABC\) .
-
A.
\(R = 26\)
-
B.
\(R = 13\)
-
C.
\(R = \dfrac{{13}}{2}\)
-
D.
\(R = 6\)
Đáp án : C
Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
Sử dụng định lý Pytago để tính toán
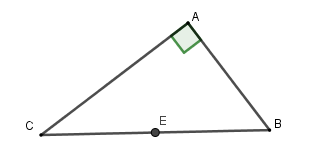
Vì tam giác \(ABC\) vuông tại\(A\) nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền \(BC\), bán kính là \(R = \dfrac{{BC}}{2}\).
Theo định lý Pytago ta có \(BC = \sqrt {A{C^2} + A{B^2}} = 13\) nên bán kính \(R = \dfrac{{13}}{2}\).
Cho đường tròn \(\left( {O;R} \right)\) có hai dây \(AB,CD\) vuông góc với nhau ở \(M\). Biết\(\,CD = 8\,cm;\,MC = 1\,cm\). Khoảng cách từ tâm \(O\) đến dây \(AB\) là
-
A.
\(4\,cm\)
-
B.
\(5\,cm\)
-
C.
\(3\,cm\)
-
D.
\(2\,cm\)
Đáp án : C
Kẻ các đường vuông góc từ tâm đến dây.
Sử dụng mối liên hệ giữa dây và đường kính và tính chất hình chữ nhật để suy ra khoảng cách.
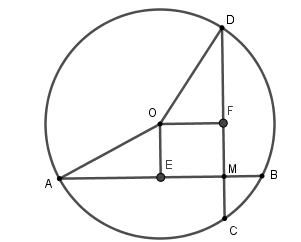
Xét đường tròn tâm \(\left( O \right)\),
Kẻ \(OE \bot AB\) tại \(E\) suy ra \(E\) là trung điểm của \(AB\), kẻ \(OF \bot CD\) tại \(F\) suy ra \(F\) là trung điểm của \(CD\),
Xét tứ giác \(OEMF\) có \(\widehat E = \widehat F = \widehat M = 90^\circ \) nên \(OEIF\) là hình chữ nhật, suy ra \(FM = OE\).
Ta có \(CD = 8\,cm \Rightarrow FC = 4\,cm\) mà \(MC = 1\,cm \Rightarrow FM = FC - MC = 4 - 1 = 3\,cm\) nên \(OE = FM = \,3cm\)
Vậy khoảng cách từ tâm \(O\) đến dây \(AB\) là \(3\,cm\)
Cho các đường tròn \(\left( {A;10\,{\rm{cm}}} \right),{\rm{ }}\left( {B;15\,{\rm{cm}}} \right),{\rm{ }}\left( {C;15\,cm} \right)\) tiếp xúc ngoài với nhau đôi một. Hai đường tròn (B) và (C) tiếp xúc với nhau tại \(A'\). Đường tròn \(\left( A \right)\) tiếp xúc với đường tròn \(\left( B \right)\) và \(\left( C \right)\) lần lượt tại \(C'\) và \(B'.\)
Chọn câu đúng nhất.
-
A.
\(AA'\) là tiếp tuyến chung của đường tròn \(\left( B \right)\) và \(\left( C \right).\)
-
B.
\(AA' = 25\,cm\)
-
C.
\(AA' = 15\,cm\)
-
D.
Cả A và B đều đúng
Đáp án: A
+ Sử dụng cách chứng minh tiếp tuyến: Đường thẳng \(d\) là tiếp tuyến của \(\left( O \right)\) tại \(A\) nếu \(d \bot OA\) tại \(A.\)
+ Sử dụng định lý Pytago để tính \(AA'\)
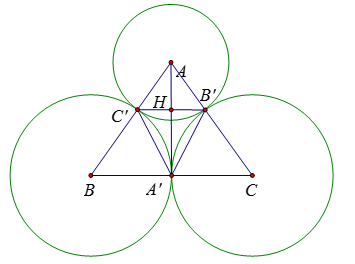
+) Theo tính chất đoạn nối tâm của hai đường tròn tiếp xúc ngoài ta có:
\(AB = BC' + C'A = 25\,cm;{\rm{ }}AC = AB' + B'C = 25\,cm;\) \({\rm{ }}BC = BA' + A'C = 30cm\) và \(A'\) là trung điểm của \(BC\) (vì \(A'B = A'C = 15cm\))
\(\Delta ABC\) cân tại \(A\) có \(AA'\) là đường trung tuyến nên cũng là đường cao
\( \Rightarrow AA' \bot BC\)
\( \Rightarrow AA'\) là tiếp tuyến chung của hai đường tròn (B) và (C)
Xét tam giác \(AA'C\) vuông tại \(A'\) có:
\(\;A'{A^2}\; = {\rm{ }}A{C^2}\; - {\rm{ }}A'{C^2}\; = {\rm{ }}{25^2} - {\rm{ }}{15^2}\; = 400\)\( \Rightarrow A'A{\rm{ }} = {\rm{ }}20\,cm\)
Tính diện tích tam giác \(A'B'C'.\)
-
A.
\(36\,c{m^2}\)
-
B.
\(72\,c{m^2}\)
-
C.
\(144\,c{m^2}\)
-
D.
\(96\,c{m^2}\)
Đáp án: B
+ Sử dụng định lý Ta-lét
+ Sử dụng công thức tính diện tích tam giác bằng nửa tích đường cao và cạnh đáy tương ứng
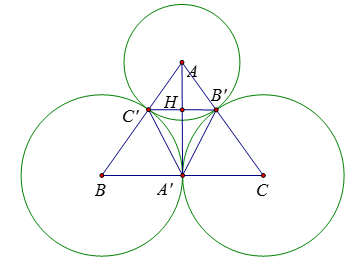
Ta có: \(\dfrac{{AC'}}{{AB}} = \dfrac{{AB'}}{{AC}} = \dfrac{{10}}{{25}} = \dfrac{2}{5}\)
\( \Rightarrow B'C'{\rm{ }}//{\rm{ }}BC\) do đó \(B'C' \bot AA'\)
Lại có: \(\dfrac{{B'C'}}{{BC}} = \dfrac{{AC'}}{{AB}} \Rightarrow \dfrac{{B'C'}}{{30}} = \dfrac{2}{5} \Leftrightarrow B'C' = 12\,cm\)
Xét \(\Delta ABA'\) có \(B'C'{\rm{ }}//{\rm{ }}BC\) nên theo định lý Ta-let ta có \(\dfrac{{AH}}{{A'A}} = \dfrac{{BC'}}{{BA}} \Rightarrow \dfrac{{AH}}{{20}} = \dfrac{{15}}{{25}} \Rightarrow AH = 12\,cm\) (do theo câu trước thì \(AA' = 20\,cm\) )
Diện tích tam giác \(A'B'C'\) là: \(S = \dfrac{1}{2}B'C'.AH = \dfrac{1}{2}.12.12 = 72\,\left( {c{m^2}} \right)\)
Cho hình vuông \(ABCD.\) Gọi \(M,N\) lần lượt là trung điểm của \(AB,BC\) . Gọi \(E\) là giao điểm của \(CM\) và \(DN\) . So sánh \(AE\) và \(DM.\)
-
A.
\(AM = \dfrac{3}{2}AE\)
-
B.
\(DM < AE\)
-
C.
\(DM = AE\)
-
D.
\(DM > AE\)
Đáp án : D
Bước 1: Đưa các điểm đã cho về các đỉnh của tam giác vuông.
Bước 2: Tìm đường tròn đi qua bốn đỉnh \(A,D,E,M\).
Bước 3: Sử dụng liên hệ giữa dây và đường kính.
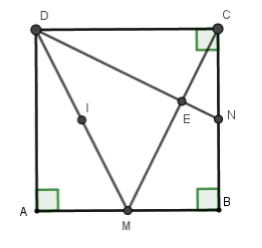
+) Ta có \(\widehat {CDN} = \widehat {ECN}\) (vì cùng phụ với \(\widehat {CNE}\)) nên \(\widehat {CNE} + \widehat {ECN} = \widehat {CNE} + \widehat {CDN} = 90^\circ \) suy ra \(\widehat {CEN} = 90^\circ \Rightarrow CM \bot DN\)
+) Gọi \(I\) là trung điểm của \(DM\).
Xét tam giác vuông \(ADM\) ta có \(AI = ID = IM = \dfrac{{DM}}{2}\). Xét tam giác vuông \(DEM\) ta có \(EI = ID = IM = \dfrac{{DM}}{2}\)
Nên \(EI = ID = IM = IA = \dfrac{{DM}}{2}\)
Do đó bốn điểm \(A,D,E,M\) cùng thuộc đường tròn tâm \(I\) bán kính \(R = \dfrac{{DM}}{2}\).
Xét \(\left( {I;\dfrac{{DM}}{2}} \right)\) có \(DM\) là đường kính và \(AE\) là dây không đi qua tâm nên \(DM > AE\).
Cho tam giác $ABC$ cân tại $A$; đường cao $AH$ và $BK$ cắt nhau tại $I$. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính $AI$.
-
A.
$HK$
-
B.
$IB$
-
C.
$IC$
-
D.
$AC$
Đáp án : A
Sử dụng cách chứng minh tiếp tuyến
Để chứng minh đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm là $M$ ta chứng minh $OM \bot d$ tại $M$ và $M \in \left( O \right)$.
Gọi $O$ là trung điểm $AI$. Xét tam giác vuông $AIK$ có $OK = OI = OA \Rightarrow K \in \left( {O;\dfrac{{AI}}{2}} \right)$ (*)
Ta đi chứng minh $OK \bot KH$ tại $K$.
Xét tam giác $OKA$ cân tại $O$ ta có $\widehat {OKA} = \widehat {OAK}$ $\left( 1 \right)$
Vì tam giác $ABC$ cân tại $A$ có đường cao $AH$ nên $H$ là trung điểm của$BC$ . Xét tam giác vuông $BKC$ có $HK = HB = HC = \dfrac{{BC}}{2}$
Suy ra tam giác $KHB$ cân tại $H$ nên $\widehat {HKB} = \widehat {HBK}$$\left( 2 \right)$
Mà $\widehat {HBK} = \widehat {KAH}$ (cùng phụ với $\widehat {ACB}$) $\left( 3 \right)$
Từ $\left( 1 \right);\left( 2 \right);\left( 3 \right)$ suy ra $\widehat {HKB} = \widehat {AKO}$ mà $\widehat {AKO} + \widehat {OKI} = 90^\circ \Rightarrow \widehat {HKB} + \widehat {OKI} = 90^\circ \Rightarrow \widehat {OKH} = 90^\circ $ hay $OK \bot KH$ tại $K$ (**)
Từ (*) và (**) thì $HK$ là tiếp tuyến của đường tròn đường kính $AI$.
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Đường tròn đường kính $BH$ cắt $AB$ tại $D$, đường tròn đường kính $CH$ cắt $AC$ tại $E$ . Chọn khẳng định sai trong các khẳng định sau
-
A.
$DE$ là cát tuyến của đường tròn đường kính $BH$
-
B.
$DE$ là tiếp tuyến của đường tròn đường kính $BH$
-
C.
Tứ giác$AEHD$ là hình chữ nhật
-
D.
$DE \bot DI$ (với $I$ là trung điểm $BH$)
Đáp án : A
Sử dụng dấu hiệu nhận biết các hình đặc biệt và cách chứng minh một đường thẳng là tiếp tuyến của đường tròn.
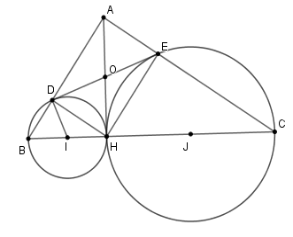
Gọi $I$, $J$ lần lượt là trung điểm của $BH$ và $CH.$
Để chứng minh $DE$ là tiếp tuyến của đường tròn tâm $I$ đường kính $BH$ ta chứng minh
\(ID \bot DE\) hay $\widehat {ODI} = {90^o}$
Vì $D,E$ lần lượt thuộc đường tròn đường kính $BH$ và $HC$ nên ta có: $\widehat {BDH} = \widehat {CEH} = {90^0}$
Suy ra tứ giác $ADHE$ là hình chữ nhật.
Gọi $O$ là giao điểm của $AH$ và$DE$, khi đó ta có $OD = OH = OE = OA$ .
Suy ra $\Delta ODH$ cân tại $O \Rightarrow \widehat {ODH} = \widehat {OHD}$
Ta cũng có $\Delta IDH$ cân tại $I$$ \Rightarrow \widehat {IDH} = \widehat {IHD}$
Từ đó $ \Rightarrow \widehat {IDH} + \widehat {HDO} = \widehat {IHD} + \widehat {DHO} \Rightarrow \widehat {IDO} = 90^\circ $$ \Rightarrow ID \bot DE$
Ta có \(ID \bot DE,D \in \left( I \right)\) nên $DE$ là tiếp tuyến của đường tròn đường kính $BH$.
Từ chứng minh trên suy ra các phương án B,C,D đúng.
Trên mặt phẳng tọa độ $Oxy$, cho điểm $A\left( {4;5} \right)$. Hãy xác định vị trí tương đối của đường tròn $\left( {A;5} \right)$ và các trục tọa độ.
-
A.
Trục tung cắt đường tròn và trục hoành tiếp xúc với đường tròn.
-
B.
Trục hoành cắt đường tròn và trục tung tiếp xúc với đường tròn
-
C.
Cả hai trục tọa độ đều cắt đường tròn
-
D.
Cả hai trục tọa độ đều tiếp xúc với đường tròn.
Đáp án : A
Bước 1: Xác định khoảng cách từ tâm $A$ đến các trục tọa độ.
Bước 2: Sử dụng vị trí tương đối giữa đường thẳng và đường tròn.
Vì $A\left( {4;5} \right)$ nên khoảng cách từ $A$ đến trục hoành là ${d_1} = \left| {{y_A}} \right| = 5$, khoảng cách từ $A$ đến trục tung là ${d_2} = \left| {{x_A}} \right| = 4$
Nhận thấy ${d_2} = R\left( { = 5} \right)$ nên trục hoành tiếp xúc với đường tròn $\left( {A;5} \right)$.
Và ${d_2} = 4 < 5 = R$ nên trục tung cắt đường tròn $\left( {A;5} \right)$.
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai ?
-
A.
$AC = CB$
-
B.
$\widehat {CBO'} = 90^\circ $
-
C.
$CA,CB$ là hai tiếp tuyến của $\left( {O'} \right)$
-
D.
$CA,CB$ là hai cát tuyến của $\left( {O'} \right)$
Đáp án : D
Sử dụng cách chứng minh một đường thẳng là tiếp tuyến của đường tròn.
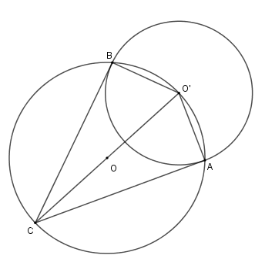
Xét đường tròn $\left( O \right)$ có $O'C$ là đường kính, suy ra $\widehat {CBO'} = \widehat {CAO'} = 90^\circ $ hay $CB \bot O'B$ tại $B$ và $AC \bot AO'$ tại $A$.
Do đó $AB,BC$ là hai tiếp tuyến của $\left( {O'} \right)$ nên $AC = CB$ (tính chất hai tiếp tuyến cắt nhau)
Nên A, B, C đúng.
Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\)tiếp xúc ngoài tại \(A\). Kẻ các đường kính \(AOB;AO'C\). Gọi \(DE\) là tiếp tuyến chung của hai đường tròn \(\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)\). Gọi \(M\) là giao điểm của \(BD\) và \(CE\). Tính diện tích tứ giác \(ADME\) biết \(\widehat {DOA} = 60^\circ \) và \(OA = 8\,cm\)
-
A.
\(12\sqrt 3 \,\,c{m^2}\)
-
B.
\( \dfrac{64}{3}\sqrt 3 \,\,c{m^2}\)
-
C.
\( \dfrac{32}{3}\sqrt 3 \,\,c{m^2}\)
-
D.
\(36\,\,c{m^2}\)
Đáp án : B
Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và hệ thức lượng trong tam giác vuông.
Diện tích hình chữ nhật bằng tích chiều dài và chiều rộng.
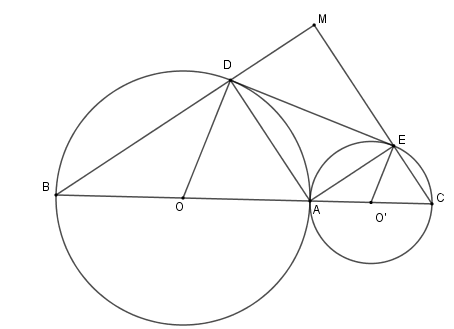
Xét \(\left( O \right)\) có \(OD = OA \Rightarrow \Delta OAD\) cân tại \(O \Rightarrow \widehat {ODA} = \widehat {OAD}\)
Xét \(\left( {O'} \right)\) có \(O'E = O'A \Rightarrow \Delta O'EB\) cân tại \(O' \Rightarrow \widehat {O'EA} = \widehat {O'AE}\)
Mà \(\widehat O + \widehat {O'} = 360^\circ - \widehat {O'ED} - \widehat {ODE} = 180^\circ \)
\( \Leftrightarrow 180^\circ - \widehat {ODA} - \widehat {OAD} + 180^\circ - \widehat {O'EA} - \widehat {O'AE} = 180^\circ \Leftrightarrow 2\left( {\widehat {OAD} + \widehat {O'AE}} \right) = 180^\circ \)
\( \Rightarrow \widehat {OAD} + \widehat {O'AE} = 90^\circ \)\( \Rightarrow \widehat {DAE} = 90^\circ \Rightarrow \Delta ADE\) vuông tại \(A\).
Mà \(\widehat {BDA} = 90^\circ \) ( vì tam giác \(BAD\) có cạnh \(AB\) là đường kính của \(\left( O \right)\)và \(D \in \left( O \right)\) ) nên \(BD \bot AD \Rightarrow \widehat {MDA} = 90^\circ \)
Tương tự ta có \(\widehat {MEA} = 90^\circ \) .\(\)\(\)
Nên tứ giác \(DMEA\) là hình chữ nhật.
Xét tam giác \(OAD\) cân tại \(O\) có \(\widehat {DOA} = 60^\circ \) nên \(\Delta DOA\) đều, suy ra \(OA = AD = 8\,cm\) và \(\widehat {ODA} = 60^\circ \)
\( \Rightarrow \widehat {ADE} = 30^\circ \). Xét tam giác \(ADE\) ta có \(EA = AD.\tan \widehat {EDA} = 8.\tan 30^\circ = \dfrac{8}{3}\sqrt 3 \)
\({S_{DMEA}} = AD.AE = 8.\dfrac{8}{3}\sqrt 3 = \dfrac{64}{3}\sqrt 3 \,\,c{m^2}\).
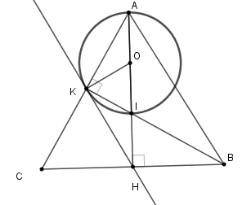
Cho đường tròn \(\left( {O;R} \right)\) và điểm A nằm ngoài \(\left( O \right)\). Từ A kẻ hai tiếp tuyến AB, AC với \(\left( O \right)\) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với \(\left( O \right)\) (E không trùng với D).
Chọn câu đúng nhất.
-
A.
Bốn điểm A, B, O, C cùng thuộc một đường tròn đường kính AC
-
B.
BC là đường trung trực của OA
-
C.
Cả A, B đều đúng.
-
D.
Cả A, B đều sai
Đáp án: D
+ Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền
+ Áp dụng tính chất hai tiếp tuyến cắt nhau và tính chất của tam giác cân để chứng minh
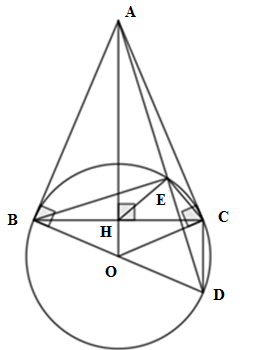
* Ta có AB, AC là hai tiếp tuyến của \(\left( O \right)\)\( \Rightarrow \angle OBA = \angle OCA = {90^o}\)
\( \Rightarrow \) B, C cùng thuộc đường tròn đường kính OA
\( \Rightarrow \) A, B, O, C cùng thuộc một đường tròn đường kính OA. Do đó A sai.
* Ta có AB, AC là hai tiếp tuyến của \(\left( O \right)\) cắt nhau tại A
\( \Rightarrow \) \(AB = AC\) và AO là phân giác \(\angle BAC\) (tính chất 2 tiếp tuyến cắt nhau)
\( \Rightarrow \Delta ABC\) là tam giác cân tại A
\( \Rightarrow \) AO vừa là phân giác \(\angle BAC\) vừa là đường trung trực của BC (tính chất tam giác cân) nên B sai.
Tỉ số \(\dfrac{{DE}}{{BE}}\) bằng
-
A.
\(\dfrac{{DA}}{{BA}}\)
-
B.
\(\dfrac{{BA}}{{DA}}\)
-
C.
\(\dfrac{{BD}}{{BA}}\)
-
D.
\(\dfrac{{BA}}{{BD}}\)
Đáp án: C
Sử dụng tam giác đồng dạng theo trường hợp góc – góc
Chứng minh \(\Delta BED\) và \(\Delta ABD\) là hai tam giác đồng dạng từ đó suy ra hệ thức đúng.
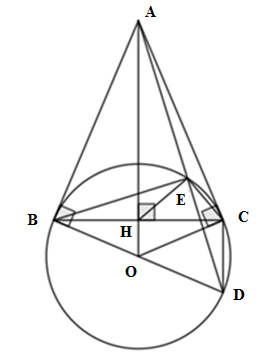
Ta có D đối xứng với B qua O \( \Rightarrow \) BD là đường kính của \(\left( O \right)\) mà \(E \in \left( O \right)\)
\( \Rightarrow \) \(\angle BED = {90^o}\)
Xét \(\Delta BED\) và \(\Delta ABD\) có: \(\angle BED = \angle ABD = {90^o}\), \(\angle D\) chung
\( \Rightarrow \Delta BED \backsim \Delta ABD\left( {g - g} \right) \Rightarrow \dfrac{{DE}}{{BE}} = \dfrac{{BD}}{{BA}}.\)
Số đo góc \(HEC\) là
-
A.
\(60^\circ \)
-
B.
\(80^\circ \)
-
C.
\(45^\circ \)
-
D.
\(90^\circ \)
Đáp án: D
Sử dụng các cặp tam giác đồng dạng để tính số đo góc.
+ Chứng minh \(\Delta BCD \backsim \Delta AHB\)
+ Chứng minh \(\Delta BHE \backsim \Delta DCE\)
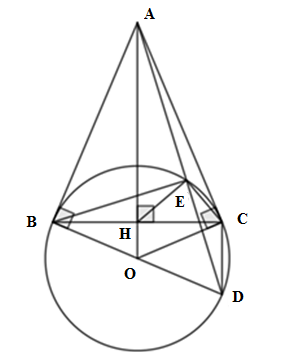
\(\angle BCD = {90^o}\) (góc nội tiếp chắn nửa đường tròn)
\(\angle AHB = {90^o}\) (AO là trung trực của BC)
Xét \(\Delta BCD\) và \(\Delta AHB\) có: \(\angle BCD = \angle AHB = {90^o},\;\angle BDC = \angle ABH\) (BA là tiếp tuyến của \(\left( O \right)\) tại B)
\( \Rightarrow \Delta BCD \backsim \Delta AHB\;\left( {g - g} \right) \)\(\Rightarrow \dfrac{{BD}}{{BA}} = \dfrac{{CD}}{{BH}}\) mà theo câu trước \(\dfrac{{DE}}{{BE}} = \dfrac{{BD}}{{BA}}\) \( \Rightarrow \dfrac{{DE}}{{BE}} = \dfrac{{CD}}{{BH}}\)
Xét \(\Delta BHE\) và \(\Delta DCE\) có \(\dfrac{{DE}}{{BE}} = \dfrac{{CD}}{{BH}}\)\( \Rightarrow \Delta BHE \backsim \Delta DCE \Rightarrow \angle BEH = \angle DEC\) (2 góc tương ứng)
\( \Rightarrow \angle BEH + \angle HED = \angle DEC + \angle HED \)\(\Rightarrow \angle BED = \angle HEC\)
Mà \(\angle BED = {90^o}\) (chứng minh trên)
Vậy \(\angle HEC = {90^o}\)
Cho đường thẳng xy và đường tròn (O; R) không giao nhau. Gọi M là một điểm di động trên xy. Vẽ đường tròn đường kính OM cắt đường tròn (O) tại A và B. Kẻ \(OH \bot xy\) . Chọn câu đúng.
-
A.
Đường thẳng AB luôn đi qua một điểm cố định là \(H.\)
-
B.
Đường thẳng AB luôn đi qua một điểm cố định là trung điểm \(OH\) .
-
C.
Đường thẳng AB luôn đi qua một điểm cố định là giao của \(OH\) và \(AB.\)
-
D.
Đường thẳng AB luôn đi qua một điểm cố định là giao của \(OH\) và \(\left( {O;R} \right).\)
Đáp án : C
+ Sử dụng tam giác đồng dạng
+ Sử dụng hệ thức lượng trong tam giác vuông để chỉ ra các điểm và đoạn thẳng cố định.
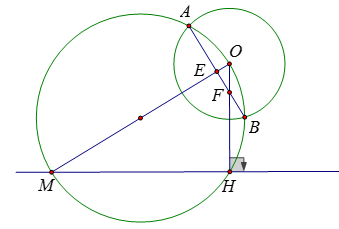
Vì \(OH \bot xy,\) nên \(H\) là một điểm cố định và \(OH\) không đổi
Gọi giao điểm của \(AB\) và \(OM\) là \(E;\) giao điểm của \(AB\) với \(OH\) là \(F.\)
Vì \(\left( {O;R} \right)\) và đường tròn đường kính \(OM\) cắt nhau tại \(A;B\) nên \(AB \bot OM\)
Lại có điểm A nằm trên đường tròn đường kính OM nên \(\widehat {OAM} = 90^\circ \)
Xét \(\Delta OEF\) và \(\Delta OHM\) có \(\widehat O\) chung và \(\widehat {OEF} = \widehat {OHM} = 90^\circ \) nên \(\Delta OEF \backsim \Delta OHM\left( {g - g} \right)\)
Suy ra \(\dfrac{{OE}}{{OH}} = \dfrac{{OF}}{{OM}} \Rightarrow OE.OM = OF.OH\)
Xét \(\Delta MAO\) vuông tại \(A\) có \(AE\) là đường cao nên theo hệ thức lượng trong tam giác vuông ta có
\(\begin{array}{*{20}{l}}{OM.OE = O{A^2}\; = {R^2}}\\{\; \Rightarrow OF.OH = {R^2}\; \Rightarrow OF = \dfrac{{{R^2}}}{{OH}}}\end{array}\)
Do \(OH\) không đổi nên \(OF\) cũng không đổi
Vậy \(F\) là một điểm cố định hay \(AB\) luôn đi qua một điểm cố định là giao của \(AB\) và \(OH.\)