Đề kiểm tra 45 phút chương 2: Hàm số bậc nhất - Đề số 1 — Không quảng cáo

Đồ thị hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ là một đường thẳng

Trường hợp 1: Nếu \(b = 0\) ta có hàm số \(y = ax\). Đồ thị của \(y = ax\) là đường thẳng đi qua gốc tọa độ \(O(0;0)\) và điểm \(A(1;a).\)

Trường hợp 2: Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right).\)

Sử dụng vị trí tương đối giữa hai đường thẳng

Cho hai đường thẳng $d:y = ax + b\,\,\left( {a \ne 0} \right)$ và $d':y = a'x + b'\,\,\left( {a' \ne 0} \right)$.

+) $d{\rm{//}}d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.$

+) \(d\)cắt$d'$\( \Leftrightarrow a \ne a'\).

+) \(d \equiv d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b = b'\end{array} \right.\).

+) \(d \bot d' \Leftrightarrow a.a' =  - 1\).

Ta thấy $d:y = x + 3$ có $a = 1$ và $d':y =  - 2x$ có $a' =  - 2$$ \Rightarrow a \ne a'\left( {1 \ne  - 2} \right)$ nên $d$ cắt $d'$.

Cho đường thẳng \(d\) có phương trình \(y = ax + b\,\left( {a \ne 0} \right)\) .

Gọi \(\alpha \) là góc tạo bởi tia \(Ox\) và \(d.\) Ta có: $a = \tan \alpha $

Bước 1: Thay tọa độ điểm $A$ vào phương trình đường thẳng $d$ để tìm $m$ và đưa phương trình về dạng $y = ax + b$ .

Bước 2: Sử dụng  lý thuyết về hệ số góc của đường thẳng.

Đường thẳng $d$ có phương trình \(y = ax + b\,\left( {a \ne 0} \right)\) có $a$ là hệ số góc.

Thay tọa độ điểm $A$ vào phương trình đường thẳng $d$ ta được $\left( {m + 2} \right).\left( { - 1} \right) - 5 = 2 \Leftrightarrow -m-2=7\Leftrightarrow m = -9$

Suy ra $d:y = -7x - 5$

Hệ số góc của đường thẳng $d$ là $k = -7$ .

Cho hàm số $y = f\left( x \right)$ xác định trên tập $D$. Khi đó : - Hàm số đồng biến trên $D \Leftrightarrow \forall {x_1},{x_2} \in D:{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)$. - Hàm số nghịch biến trên $D \Leftrightarrow \forall {x_1},{x_2} \in D:{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)$

Đồ thị hàm số \(y = ax + b(a \ne 0)\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi và chỉ khi \({y_0} = a{x_0} + b\)

Thay tọa độ từng điểm vào hàm số ta được

+) Với $A\left( {\dfrac{{ - 5}}{3};0} \right)$. Thay $x =  - \dfrac{5}{3};y = 0$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( { - \dfrac{5}{3} - 1} \right) + \dfrac{4}{3} = 0 \Leftrightarrow \dfrac{{ - 20}}{3} = 0$ (Vô lý)

+) Với $B\left( {1;\dfrac{3}{4}} \right)$. Thay $x = 1;y = \dfrac{3}{4}$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( {1 - 1} \right) + \dfrac{4}{3} = \dfrac{3}{4} \Leftrightarrow \dfrac{4}{3} = \dfrac{3}{4}$ (Vô lý)

+) Với $D\left( {4;\dfrac{4}{3}} \right)$. Thay $x = 4;y = \dfrac{4}{3}$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( {4 - 1} \right) + \dfrac{4}{3} = \dfrac{4}{3} \Leftrightarrow \dfrac{{31}}{3} = \dfrac{4}{3}$ (Vô lý)

+)Với $C\left( { \dfrac{2}{3};\dfrac{1}{3}} \right)$. Thay $x =  \dfrac{2}{3};y = \dfrac{1}{3}$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( { \dfrac{2}{3} - 1} \right) + \dfrac{4}{3} = \dfrac{1}{3} \Leftrightarrow \dfrac{1}{3} = \dfrac{1}{3}$ (luôn đúng)

$ \Rightarrow C$ thuộc đồ thị hàm số $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$

Sử dụng cách tính giá  trị hàm số tại một điểm

Để tính giá trị ${y_0}$ của hàm số $y = f\left( x \right)$ tại điểm ${x_0}$ ta thay $x = {x_0}$ vào $f\left( x \right)$, ta được ${y_0} = f\left( {{x_0}} \right)$.

Thay $x = 3$ vào hàm số ta được $f\left( 3 \right) = {3^3} - 3.3 - 2 = 16$$ \Rightarrow 2.f\left( 3 \right) = 2.16 = 32$ .

Sử dụng cách tính giá  trị hàm số tại một điểm

Để tính giá trị ${y_0}$ của hàm số $y = f\left( x \right)$ tại điểm ${x_0}$ ta thay $x = {x_0}$ vào $f\left( x \right)$, ta được ${y_0} = f\left( {{x_0}} \right)$.

So sánh các giá trị tìm được

Thay $x =  - 2$ vào hàm số $f\left( x \right) =  - 2{x^3}$ ta được $f\left( { - 2} \right) =  - 2.{\left( { - 2} \right)^3} = 16$ .

Thay $x =  - 1$ vào hàm số $h\left( x \right) = 10 - 3x$ ta được $h\left( { - 1} \right) = 10 - 3\left( { - 1} \right) = 13$

Nên $f\left( { - 2} \right) > h\left( { - 1} \right)$ .

Điểm \(M\left( {{x_0};{y_0}} \right)\) thuộc đồ thị hàm số \(y = f\left( x \right)\) khi \({y_0} = f\left( {{x_0}} \right)\)

Lần lượt thay tọa độ các điểm \(M,O,P,Q;A\) vào hàm số \(f\left( x \right) = 3x\) ta được

+) Với \(M\left( {1;1} \right)\), thay \(x = 1;y = 1\) ta được \(1 = 3.1 \Leftrightarrow 1 = 3\) (Vô lý) nên \(M \notin \left( C \right)\).

+) Với \(O\left( {0;0} \right)\), thay \(x = 0;y = 0\) ta được \(0 = 3.0 \Leftrightarrow 0 = 0\) (luôn đúng) nên \(O \in \left( C \right)\)

+) Với \(P\left( { - 1; - 3} \right)\), thay \(x = -1;y =  - 3\) ta được \( - 3 = 3.\left( { - 1} \right) \Leftrightarrow  - 3 =  - 3\) (luôn đúng) nên \(P \in \left( C \right)\).

+) Với \(Q\left( {3;9} \right)\), thay \(x = 3;y = 9\) ta được \(9 = 3.3 \Leftrightarrow 9 = 9\) (luôn đúng) nên \(Q \in \left( C \right)\).

+) Với \(A\left( { - 2;6} \right)\), thay \(x =  - 2;y = 6\) ta được \(6 = \left( { - 2} \right).3 \Leftrightarrow 6 =  - 6\) (vô lý) nên \(A \notin \left( C \right)\).

Vậy có ba điểm thuộc đồ thị \(\left( C \right)\) trong số các điểm đã cho.

Bước 1: Tìm tập xác định \(D\) của hàm số.

Bước 2: Giả sử \({x_1} < {x_2}\) và \({x_1},{x_2} \in D\). Xét hiệu \(H = f\left( {{x_1}} \right) - f\left( {{x_2}} \right)\).

+ Nếu \(H < 0\) với \({x_1},{x_2}\) bất kỳ thì hàm số đồng biến.

+ Nếu \(H > 0\) với \({x_1},{x_2}\) bất kỳ thì hàm số nghịch biến.

TXĐ: \(D = \mathbb{R}\)

Giả sử \({x_1} < {x_2}\) và \({x_1},{x_2} \in \mathbb{R}\) . Ta có \(f\left( {{x_1}} \right) = \dfrac{1}{2}{x_1} + 3;f\left( {{x_2}} \right) = \dfrac{1}{2}{x_2} + 3\).

Xét hiệu \(H = f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \dfrac{1}{2}{x_1} + 3 - \left( {\dfrac{1}{2}{x_2} + 3} \right)\)\( = \dfrac{1}{2}{x_1} + 3 - \dfrac{1}{2}{x_2} - 3 = \dfrac{1}{2}\left( {{x_1} - {x_2}} \right) < 0\) (vì \({x_1} < {x_2}\))

Vậy \(y = \dfrac{1}{2}x + 3\) là hàm số đồng biến.

Tìm tọa độ giao điểm của hai đường thẳng theo các bước

Bước 1. Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.

Bước 2. Thay hoành độ giao điểm vừa tìm được vào một trong hai phương trình đường thẳng ta tìm được tung độ giao điểm.

Giao điểm của đường thẳng $d$ và trục tung có hoành độ $x = 0$. Thay $x = 0$ vào phương trình $y = 3x - \dfrac{1}{2}$ ta được $y = 3.0 - \dfrac{1}{2} =  - \dfrac{1}{2}$.

Vậy tọa độ giao điểm cần tìm là $D\left( {0; - \dfrac{1}{2}} \right)$

Để hai đường thẳng ${d_1}:y = ax + b$ và ${d_2}:y = a'x + b'$ cắt nhau tại một điểm trên trục tung thì $\left\{ \begin{array}{l}a \ne a'\\b = b'\end{array} \right.$

Để hai đồ thị hàm số \(y =  - 2x + m + 2\) và \(y = 5x + 5 - 2m\) cắt nhau tại một điểm trên trục tung thì

$\left\{ \begin{array}{l} - 2 \ne 5\\m + 2 = 5 - 2m\end{array} \right.$$ \Leftrightarrow 3m = 3 \Leftrightarrow m = 1$.

Để $M\left( {{x_0};{y_0}} \right)$ là giao của hai đường thẳng ${d_1}$ và ${d_2}$ ta thay tọa độ điểm $M$ vào từng phương trình đường thẳng để tìm $m$.

+) Nhận thấy $M \in {d_2}$.

+) Ta thay tọa độ điểm $M$ vào phương trình ${d_1}$ được phương trình $ - 1 = 2.m + 1 \Leftrightarrow m =  - 1$

Vậy $m =  - 1$.

Để hai đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm có tung độ $y = {y_0}$.

Bước 1. Thay $y = {y_0}$ vào phương trình đường thẳng đã biết để tìm ${x_0}$.

Bước 2. Thay $x = {x_0}$; $y = {y_0}$ vào phương trình đường thẳng còn lại để tìm $m$.

Thay $y = 4$ vào phương trình đường thẳng ${d_2}$ ta được $x + 1 = 4 \Leftrightarrow x = 3$.

Suy ra tọa độ giao điểm của ${d_1}$ và ${d_2}$ là $\left( {3;4} \right)$.

Thay $x = 3;y = 4$ vào phương trình đường thẳng ${d_1}$ ta được $\left( {m + 1} \right).3 - 1 = 4 \Leftrightarrow m + 1 = \dfrac{5}{3} \Leftrightarrow m = \dfrac{2}{3}$.

Vậy $m = \dfrac{2}{3}$.

+) Tìm điều kiện để hàm số $y=ax+b$ là hàm số bậc nhất là $a\ne 0$

+) Sử dụng vị trí tương đối giữa hai đường thẳng:

Cho hai đường thẳng $d:y = ax + b\,\,\left( {a \ne 0} \right)$ và $d':y = a'x + b'\,\,\left( {a' \ne 0} \right)$.

+) $d{\rm{//}}d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.$

+) \(d\) cắt $d'$\( \Leftrightarrow a \ne a'\).

+) \(d \equiv d' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b = b'\end{array} \right.\).

+) \(d \bot d' \Leftrightarrow a.a' =  - 1\).

+) Ta thấy $d:y = \left( {m + 2} \right)x - m$ có $a = m + 2$ và $d':y =  - 2x - 2m + 1$ có $a' =  - 2$ .

+) Để $y = \left( {m + 2} \right)x - m$ là hàm số bậc nhất thì $m + 2 \ne 0 \Leftrightarrow m \ne  - 2$

+) Để \(d\) cắt $d'$\( \Leftrightarrow a \ne a'\)

$ \Leftrightarrow m + 2 \ne  - 2 \Leftrightarrow m \ne  - 4$

Vậy $m \ne \left\{ { - 2; - 4} \right\}$.

Tìm tọa độ giao điểm của đường thẳng và các trục tọa độ

Sử dụng công thức tính diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông

Giải phương trình chứa dấu giá trị tuyệt đối để tìm \(m\)

\(\begin{array}{l}d \cap Oy = \left\{ B \right\}\\x_B = 0 \Rightarrow y_B =  - 1\\ \Rightarrow B(0; - 1) \Rightarrow OB = | - 1| = 1\\d \cap {\rm{Ox}} = \left\{ A \right\}\\y_A = 0 \Leftrightarrow (k - 2)x_A - 1 = 0 \Leftrightarrow x_A = \dfrac{1}{{k - 2}}(k \ne 2)\\ \Rightarrow A\left( {\dfrac{1}{{k - 2}};0} \right) \Rightarrow OA = \left| {\dfrac{1}{{k - 2}}} \right|\end{array}\)

\(\begin{array}{l}{S_{\Delta AOB}} = \dfrac{1}{2}OA.OB = 1 \Leftrightarrow \dfrac{1}{2}.1.\left| {\dfrac{1}{{k - 2}}} \right| = 1\\ \Leftrightarrow |k - 2| = \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}k = \dfrac{5}{2}\\k = \dfrac{3}{2}\end{array} \right.(tmdk)\end{array}\)

Bước 1: Gọi phương trình đường thẳng cần tìm là \(y = ax + b\,\,\left( {a \ne 0} \right)\)

Bước 2:  Tìm hệ số \(a\) theo mối quan hệ vuông góc.

Bước 3: Thay tọa độ điểm \(M\) vào phương trình đường thẳng ta tìm được \(b\).

Gọi phương trình đường thẳng \(d\) cần tìm là \(y = ax + b\,\,\left( {a \ne 0} \right)\)

Vì \(d\)\( \bot \)\(d'\) nên \(a.\dfrac{1}{5} =  - 1 \Leftrightarrow a =  - 5\left( {TM} \right)\)\( \Rightarrow d:y =  - 5x + b\)

Thay tọa độ điểm \(M\) vào phương trình đường thẳng \(d\) ta được \( - 5.\left( { - 4} \right) + b = 2 \Leftrightarrow b =  - 18\)

Vậy phương trình đường thẳng \(d:y =  - 5x - 18\).

Bước 1: Gọi phương trình đường thẳng cần tìm là \(y = ax + b\,\,\)\(\left( {a \ne 0} \right)\)

Bước 2:  Thay tọa độ hai điểm \(A,B\) vào phương trình đường thẳng \(d\) để tìm hệ số \(a,b\).

Gọi phương trình đường thẳng cần tìm là \(y = ax + b\,\,\)\(\left( {a \ne 0} \right)\)

Thay tọa độ điểm \(A\) vào phương trình đường thẳng \(d\) ta được \(3a + b = 3\)\( \Rightarrow b = 3 - 3a\)

Thay tọa độ điểm \(B\) vào phương trình đường thẳng \(d\) ta được \( - 1.a + b = 4\)\( \Rightarrow b = 4 + a\)

Suy ra \(3 - 3a = 4 + a \Leftrightarrow 4a =  - 1 \Leftrightarrow a =  - \dfrac{1}{4}\)\( \Rightarrow b = 4 + a = 4 + \left( { - \dfrac{1}{4}} \right) = \dfrac{{15}}{4} \Rightarrow y = \dfrac{{ - 1}}{4}x + \dfrac{{15}}{4}\).

Vậy \(d:y =  - \dfrac{1}{4}x + \dfrac{{15}}{4}\).

Gọi phương trình đường thẳng $d:y = ax + b$ $(a \ne 0)$

Xác định hệ số $a$ dựa vào góc tạo bởi đường thẳng $d$với đường thẳng cho trước tìm $b$ dựa vào giao điểm với trục tung.

Gọi phương trình đường thẳng $d:y = ax + b$ $(a \ne 0)$

Vì góc tạo bởi đường thẳng $d$ và đường thẳng $y = 1$ là $120^\circ $ nên góc tạo bởi đường thẳng $d$ và trục $Ox$ cũng  là $120^\circ $ (do đường thẳng $y = 1$ song song với trục $Ox$) nên $a = \tan 120^\circ  =  - \sqrt 3 $

$ \Rightarrow y =  - \sqrt 3 x + b$

Vì đường thẳng $d$ cắt trục tung tại điểm có tung độ $ - 2$ nên $ b =  - 2$.

Từ đó $d:y =  - \sqrt 3 x - 2$.

+ Sử dụng điều kiện vuông góc của hai đường thẳng để tìm $m$ .

+ Sau đó sử dụng  lý thuyết về hệ số góc để tìm hệ số góc của đường thẳng $d'$

Đường thẳng  có phương trình \(y = ax + b\,\left( {a \ne 0} \right)\) có $a$ là hệ số góc.

Ta có $d':x - 2y - 6 = 0$$ \Leftrightarrow y = \dfrac{1}{2}x - 3$

Vì $d \bot d' \Rightarrow \left( {3 - m} \right).\dfrac{1}{2} =  - 1 \Leftrightarrow 3 - m =  - 2 \Leftrightarrow m = 5$

$ \Rightarrow d:y =  - 2x + 2$ có hệ số góc $k =  - 2$

+) Thay tọa độ điểm $A$ vào phương trình đường thẳng $d$ để tìm $m$.

+) Sử dụng cách tìm hệ số góc : đường thẳng $d:y = ax + b$$\left( {a \ne 0} \right)$ có hệ số góc $a$.

Thay tọa độ điểm $A$ vào phương trình đường thẳng $d$ ta có $2\left( {m + 1} \right).3 - 5m - 8 =  - 5 \Leftrightarrow m =  - 3$

Khi đó $y =  - 4x + 7$

Đường thẳng $y =  - 4x + 7$ có hệ số góc $k =  - 4$.

Bước 1: Viết phương trình đường thẳng $d$

Bước 2: Xác định hệ số góc: đường thẳng $d$ có phương trình \(y = ax + b\,\left( {a \ne 0} \right)\) có $a$ là hệ số góc.

Gọi phương trình đường thẳng $d$ cần tìm là $y = ax + b\,$

Vì $d$ đi qua $A\left( {1;1} \right)$ nên $a + b = 1 \Rightarrow b = 1 - a$

Thay tọa độ điểm $B$ vào phương trình  ta được $ - a + b = 2$$ \Rightarrow b = a + 2$

Nên ta có $1 - a = a + 2 \Leftrightarrow a =  - \dfrac{1}{2}$$ \Rightarrow b = 1 - \left( { - \dfrac{1}{2}} \right) = \dfrac{3}{2} \Rightarrow y =  - \dfrac{1}{2}x + \dfrac{3}{2}$

Hệ số góc của $d$ là $k =  - \dfrac{1}{2}$ .

- Lập bảng giá trị để xác định 2 điểm thuộc đường thẳng.

- Xác định giao điểm 2 đường thẳng đã cho

- Tính độ dài các đoạn thẳng cần thiết

- Dựng đường cao của tam giác được tạo thành

- Tính diện tích các tam giác phụ được tạo thành

- Tính diện tích tam giác theo yêu cầu đề bài

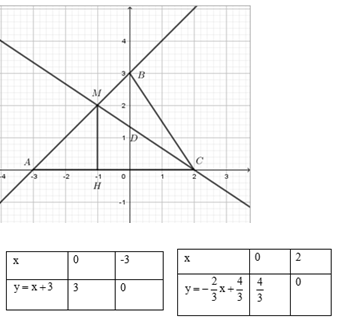
Xét phương trình hoành độ giao điểm:

$x + 3 =  - \dfrac{2}{3}x + \dfrac{4}{3} \Leftrightarrow 3x + 9 =  - 2x + 4 \Leftrightarrow 5x =  - 5 \Leftrightarrow x =  - 1 \Rightarrow y = 2$

Do đó giao điểm của $2$ đường thẳng đã cho là $M\left( { - 1;2} \right)$

$\begin{array}{l}d \cap Ox = A( - 3;0) \Rightarrow OA = 3\\d' \cap Ox = C(2;0) \Rightarrow OC = 2\\d \cap Oy = B(0;3) \Rightarrow OB = 3\\d' \cap Oy = D\left( {0;\dfrac{4}{3}} \right)\\ \Rightarrow AC = OA + OC = 3 + 2 = 5\\{S_{\Delta ABC}} = \dfrac{1}{2}AC.OB = \dfrac{1}{2}.5.3 = \dfrac{{15}}{2}(dvdt)\end{array}$

Gọi $H$ là hình chiếu của $M$ trên $Ox$

$\begin{array}{l} \Rightarrow MH = |{y_M}| = 2\\{S_{\Delta AMC}} = \dfrac{1}{2}MH.AC = \dfrac{1}{2}.2.5 = 5(dvdt)\\{S_{\Delta BMC}} = {S_{\Delta ABC}} - {S_{\Delta AMC}} = \dfrac{{15}}{2} - 5 = \dfrac{5}{2}(dvdt)\end{array}$

- Điều kiện để 2 đường thẳng cắt nhau

- Tìm tọa độ giao điểm 2 đường thẳng

- Tìm nghiệm nguyên

Ta có: $d \cap d' \Leftrightarrow m \ne 2$.

Xét phương trình hoành độ giao điểm của $d$ và $d'$ : $mx - 2 = 2x + 1 \Leftrightarrow (m - 2)x = 3 \Leftrightarrow x = \dfrac{3}{{m - 2}}$

Ta có $x = \dfrac{3}{{m - 2}} \in Z \Leftrightarrow m - 2 \in U(3) = \left\{ { \pm 1; \pm 3} \right\}$

Ta có bảng sau:

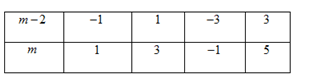
Vậy $m \in \left\{ { - 1;1;3;5} \right\}$.

\(M\left( {{x_0};{y_0}} \right)\) là điểm cố định mà d luôn đi qua\( \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d,\forall m \Leftrightarrow m.A + B = 0,\forall m \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\)

Giải hệ phương trình tìm nghiệm.

Gọi \(M\left( {{x_0};{y_0}} \right)\) là điểm cố định mà d luôn đi qua.

\(\begin{array}{l} \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d\begin{array}{*{20}{c}}{}&{}\end{array}\forall k\\ \Leftrightarrow {y_0} = \dfrac{{\sqrt k  + 1}}{{\sqrt 3  - 1}}{x_0} + \sqrt k  + \sqrt 3 \begin{array}{*{20}{c}}{}&{}\end{array}\forall k\\ \Leftrightarrow \sqrt k {x_0} + {x_0} + \sqrt {3k}  - \sqrt k  - \sqrt 3  + 3 - \sqrt 3 {y_0} + {y_0} = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall k\\ \Leftrightarrow \sqrt k ({x_0} + \sqrt 3  - 1) + {x_0} + 3 - \sqrt 3  + (1 - \sqrt 3 ){y_0} = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall k\\ \Leftrightarrow \left\{ \begin{array}{l}{x_0} + \sqrt 3  - 1 = 0\\{x_0} + (1 - \sqrt 3 ){y_0} + 3 - \sqrt 3  = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1 - \sqrt 3 \\(1 - \sqrt 3 ) + (1 - \sqrt 3 ){y_0} + 3 - \sqrt 3  = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1 - \sqrt 3 \\(1 - \sqrt 3 ){y_0} + 4 - 2\sqrt 3  = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1 - \sqrt 3 \\(1 - \sqrt 3 ){y_0} + {(1 - \sqrt 3 )^2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1 - \sqrt 3 \\{y_0} =  - 1 + \sqrt 3 \end{array} \right.\end{array}\)

\( \Rightarrow M\left( {1 - \sqrt 3 ;\sqrt 3  - 1} \right)\)là điểm cố định mà d luôn đi qua.