Đề kiểm tra 15 phút chương 6: Đường tròn - Đề số 2 — Không quảng cáo

Sử dụng  cách chứng minh tiếp tuyến

Để chứng minh đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm là $M$ ta chứng minh $OM \bot d$ tại $M$ và $M \in \left( O \right)$.

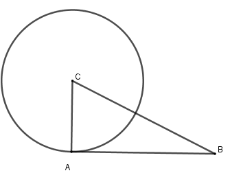
+) Xét tam giác $ABC$ có \(B{C^2} = {5^2} = 25;A{B^2} + A{C^2} = {4^2} + {3^2} = 25; \Rightarrow B{C^2} = A{B^2} + A{C^2}\)

\( \Rightarrow \Delta ABC\) vuông tại A (định lý Pytago đảo)

\( \Rightarrow AB \bot AC\) mà $A \in \left( {C;CA} \right)$ nên $AB$ là tiếp tuyến của $\left( {C;CA} \right)$

Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với phần kéo dàicủa hai cạnh còn lại gọi là đường tròn bàng tiếp tam giác.

Với một tam giác có ba đường tròn bàng tiếp.

Nếu một đường thẳng  đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.

Đường thẳng và đường tròn có nhiều nhất hai điểm chung.

Sử dụng bảng vị trí tương đối của đường thẳng và đường tròn

+) Vì \(d > R\left( {5\,cm < 3\,cm} \right)\) nên đường thẳng không cắt đường tròn hay (1) điền là: Không cắt nhau.

+) Vì đường thẳng tiếp xúc với đường tròn nên \(d = R = 9\,cm\) hay (2) điền là \(9\,cm\)

Sử dụng  cách chứng minh tiếp tuyến

Để chứng minh đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm là $M$ ta chứng minh $OM \bot d$ tại $M$ và $M \in \left( O \right)$.

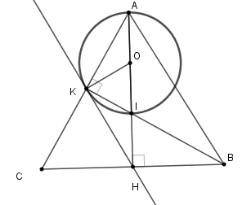
Gọi $O$ là trung điểm $AI$. Xét tam giác vuông $AIK$ có $OK = OI = OA \Rightarrow K \in \left( {O;\dfrac{{AI}}{2}} \right)$ (*)

Ta đi chứng minh $OK \bot KH$ tại $K$.

Xét tam giác $OKA$ cân tại $O$ ta có $\widehat {OKA} = \widehat {OAK}$ $\left( 1 \right)$

Vì tam giác $ABC$ cân tại $A$ có đường cao $AH$ nên $H$ là trung điểm của$BC$ . Xét tam giác vuông $BKC$ có $HK = HB = HC = \dfrac{{BC}}{2}$

Suy ra tam giác $KHB$ cân tại $H$ nên $\widehat {HKB} = \widehat {HBK}$$\left( 2 \right)$

Mà $\widehat {HBK} = \widehat {KAH}$ (cùng phụ với $\widehat {ACB}$) $\left( 3 \right)$

Từ $\left( 1 \right);\left( 2 \right);\left( 3 \right)$ suy ra $\widehat {HKB} = \widehat {AKO}$ mà $\widehat {AKO} + \widehat {OKI} = 90^\circ  \Rightarrow \widehat {HKB} + \widehat {OKI} = 90^\circ  \Rightarrow \widehat {OKH} = 90^\circ $ hay $OK \bot KH$ tại $K$ (**)

Từ (*) và (**) thì $HK$ là tiếp tuyến của đường tròn đường kính $AI$.

Xác định xem tâm đường tròn cách đường thẳng cho trước một khoảng bằng bao nhiêu rồi sử dụng tính chất tia phân giác của một góc để xác định tập hợp điểm.

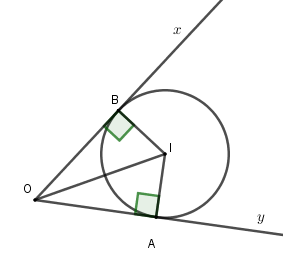
Kẻ $IA \bot Oy;IB \bot Ox$ tại $A,B$.

Vì $\left( I \right)$ tiếp xúc với cả $Ox;Oy$ nên $IA = IB$ suy ra $I$ thuộc tia phân giác của góc $\widehat {xOy}$ ($I \ne O$)

(tính chất tia phân giác của một góc)

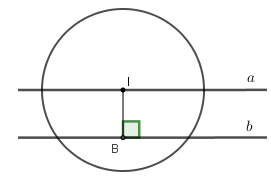
Vì hai đường thẳng song song \(a,b\) cách nhau một khoảng là \(3\,cm\) mà \(I \in a\) nên khoảng cách từ tâm \(I\) đến đường thẳng \(b\) là \(d = 3\,cm\).

Suy ra \(d < R\left( {3\,cm < 3,5\,cm} \right)\) nên đường tròn \(\left( {I;3,5cm} \right)\) và đường thẳng \(b\) cắt nhau.

Sử dụng cách chứng minh một đường thẳng là tiếp tuyến của đường tròn.

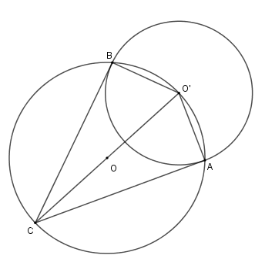
Xét đường tròn $\left( O \right)$ có $O'C$ là đường kính, suy ra $\widehat {CBO'} = \widehat {CAO'} = 90^\circ $ hay $CB \bot O'B$ tại $B$ và $AC \bot AO'$ tại $A$.

Do đó $AB,BC$ là hai tiếp tuyến của $\left( {O'} \right)$ nên $AC = CB$ (tính chất hai tiếp tuyến cắt nhau)

Nên A, B, C đúng.

Sử dụng tính chất hai tiếp tuyến cắt nhau và công thức chu vi tam giác

Sử dụng tỉ số lượng giác của góc nhọn

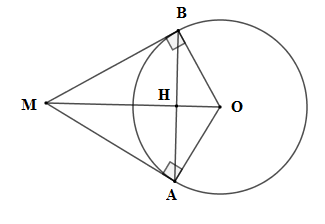
Xét \(\left( O \right)\) có \(MA = MB\) (tính chất hai tiếp tuyến cắt nhau) mà \(\widehat {AMB} = 60^\circ \) nên \(\Delta MAB\) đều suy ra chu vi \(\Delta MAB\) là \(MA + MB + AB = 3AB = 24 \)\(\Rightarrow AB = 8cm = MA = MB\)

Lại có \(\widehat {AMO} = \dfrac{1}{2}\widehat {AMB} = 30^\circ \) (tính chất 2 tiếp tuyến cắt nhau)

Xét tam giác vuông \(MAO\) có \(\tan \widehat {AMO} = \dfrac{{OA}}{{MA}} \Rightarrow OA = MA.\tan 30^\circ  = \dfrac {8}{\sqrt 3}\,cm\)