Đề kiểm tra 15 phút chương 7: Góc với đường tròn - Đề số 1
Đề bài
Góc tạo bởi tiếp tuyến và dây cung có số đo bằng
-
A.
\(90^\circ \)
-
B.
Số đo góc ở tâm chắn cung đó
-
C.
Nửa số đo của góc nội tiếp chắn cung đó
-
D.
Nửa số đo của cung bị chắn
Chọn khẳng định đúng. Trong một đường tròn, số đo cung nhỏ bằng
-
A.
Số đo cung lớn
-
B.
Số đo của góc ở tâm chắn cung đó
-
C.
Số đo của góc ở tâm chắn cung lớn
-
D.
Số đo của cung nửa đường tròn
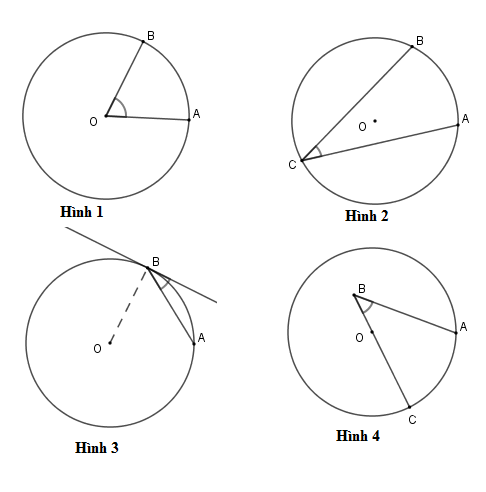
Hình nào dưới đây biểu diễn góc nội tiếp?
-
A.
Hình \(1\)
-
B.
Hình \(2\)
-
C.
Hình $3$
-
D.
Hình \(4\)
Chọn khẳng định đúng.
-
A.
Trong một đường tròn, đường kính đi qua trung điểm của một dây ( không đi qua tâm ) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
-
B.
Trong một đường tròn, đường kính đi qua trung điểm của một dây thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
-
C.
Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì song song với dây căng cung ấy
-
D.
Trong một đường tròn, hai đường kính luôn vuông góc với nhau
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng ?
-
A.
$AD > BC$
-
B.
Số đo cung $AD$ bằng số đo cung $BC$
-
C.
$AD < BC$
-
D.
$\widehat {AOD} > \widehat {COB}$
Cho tam giác $ABC$ có ba đỉnh thuộc đường tròn tâm $(O)$, đường cao $AH$, đường kính $AD.$ Khi đó tích $AB.AC$ bằng
-
A.
\(AH.HD\)
-
B.
$AH.AD$
-
C.
\(AH.HB\)
-
D.
$A{H^2}$
Cho đường tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$. Khi đó \(A{B^2}\) bằng
-
A.
\(AD.AE\)
-
B.
\(AD.AC\)
-
C.
\(AE.BE\)
-
D.
\(AD.BD\)
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) . Kẻ tiếp tuyến \(xAy\) với \(\left( O \right)\) . Từ \(B\) kẻ \(BM{\rm{//}}xy\left( {M \in AC} \right)\) . Khi đó tích $AM.AC$ bằng
-
A.
\(A{B^2}\)
-
B.
\(B{C^2}\)
-
C.
\(A{C^2}\)
-
D.
\(A{M^2}\)
Lời giải và đáp án
Góc tạo bởi tiếp tuyến và dây cung có số đo bằng
-
A.
\(90^\circ \)
-
B.
Số đo góc ở tâm chắn cung đó
-
C.
Nửa số đo của góc nội tiếp chắn cung đó
-
D.
Nửa số đo của cung bị chắn
Đáp án : D
Góc tạo bởi tiếp tuyến và dây cung có số đo bằng nửa số đo cung bị chắn
Chọn khẳng định đúng. Trong một đường tròn, số đo cung nhỏ bằng
-
A.
Số đo cung lớn
-
B.
Số đo của góc ở tâm chắn cung đó
-
C.
Số đo của góc ở tâm chắn cung lớn
-
D.
Số đo của cung nửa đường tròn
Đáp án : B
Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Hình nào dưới đây biểu diễn góc nội tiếp?

-
A.
Hình \(1\)
-
B.
Hình \(2\)
-
C.
Hình $3$
-
D.
Hình \(4\)
Đáp án : B
Sử dụng định nghĩa góc nội tiếp:
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
Hình \(1\) góc \(\widehat {BOA}\) là góc ở tâm .
Hình \(3\) có \(1\) cạnh không phải là dây của đường tròn.
Hình \(4\) đỉnh $B$ không nằm trên đường tròn.
Hình \(2\) góc \(\widehat {BCA}\) là góc nội tiếp chắn cung \(AB\)
Chọn khẳng định đúng.
-
A.
Trong một đường tròn, đường kính đi qua trung điểm của một dây ( không đi qua tâm ) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
-
B.
Trong một đường tròn, đường kính đi qua trung điểm của một dây thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
-
C.
Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì song song với dây căng cung ấy
-
D.
Trong một đường tròn, hai đường kính luôn vuông góc với nhau
Đáp án : A
+) Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.
+) Trong một đường tròn, đường kính đi qua trung điểm của một dây ( không đi qua tâm ) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
+) Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng ?
-
A.
$AD > BC$
-
B.
Số đo cung $AD$ bằng số đo cung $BC$
-
C.
$AD < BC$
-
D.
$\widehat {AOD} > \widehat {COB}$
Đáp án : B
Sử dụng liên hệ giữa dây và đường kính để so sánh các góc ở tâm từ đó so sánh các cung và dây cung.
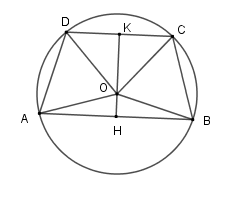
Kẻ $KH \bot CD$ và $KH \bot AB$ lần lượt tại $K$ và $H$.
Suy ra $OK$ vừa là đường cao, vừa là đường phân giác của $\widehat {DOC}$ $ \Rightarrow \widehat {DOK} = \widehat {COK}$
Và $OH$ vừa là đường cao, vừa là đường phân giác của $\widehat {AOB}$ $ \Rightarrow \widehat {AOH} = \widehat {BOH}$
Do đó $\widehat {AOH} + \widehat {DOK} = \widehat {BOH} + \widehat {COK} \Rightarrow \widehat {AOD} = \widehat {COB}$
Nên số đo cung $AD$ bằng số đo cung $BC$, từ đó $AD = BC$.
Phương án A, C, D sai, B đúng.
Cho tam giác $ABC$ có ba đỉnh thuộc đường tròn tâm $(O)$, đường cao $AH$, đường kính $AD.$ Khi đó tích $AB.AC$ bằng
-
A.
\(AH.HD\)
-
B.
$AH.AD$
-
C.
\(AH.HB\)
-
D.
$A{H^2}$
Đáp án : B
Sử dụng tính chất góc nội tiếp để chứng minh các góc bằng nhau để chứng minh hai tam giác đồng dạng.
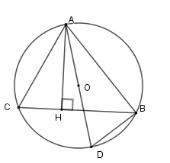
Xét \(\left( O \right)\) có \(\widehat {ACB} = \widehat {ADB}\) (hai góc nội tiếp cùng chắn cung \(AB\) ); \(\widehat {ABD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Nên \(\Delta ACH \backsim \Delta ADB\left( {g - g} \right)\)
Suy ra $\dfrac{{AC}}{{AD}} = \dfrac{{AH}}{{AB}} $
Do đó $AH.AD = AC.AB$.
Cho đường tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$. Khi đó \(A{B^2}\) bằng
-
A.
\(AD.AE\)
-
B.
\(AD.AC\)
-
C.
\(AE.BE\)
-
D.
\(AD.BD\)
Đáp án : A
Sử dụng hệ quả của góc nội tiếp để chứng minh các góc bằng nhau và suy ra tam giác đồng dạng
Từ đó có hệ thức cần chứng minh.
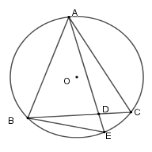
Xét \(\left( O \right)\) có \(\widehat {AEB} = \widehat {ABC}\) (hai góc nội tiếp chắn hai cung bằng nhau \(AB = AC\) )
Xét \(\Delta ABD\) và \(\Delta AEB\) có \(\widehat A\) chung và \(\widehat {AEB} = \widehat {ABC}\) (cmt) nên \(\Delta ABD\backsim\Delta AEB\left( {g - g} \right) \Rightarrow \dfrac{{AB}}{{AE}} = \dfrac{{AD}}{{AB}} \Rightarrow A{B^2} = AE.AD\)
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) . Kẻ tiếp tuyến \(xAy\) với \(\left( O \right)\) . Từ \(B\) kẻ \(BM{\rm{//}}xy\left( {M \in AC} \right)\) . Khi đó tích $AM.AC$ bằng
-
A.
\(A{B^2}\)
-
B.
\(B{C^2}\)
-
C.
\(A{C^2}\)
-
D.
\(A{M^2}\)
Đáp án : A
Sử dụng hệ quả về góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau
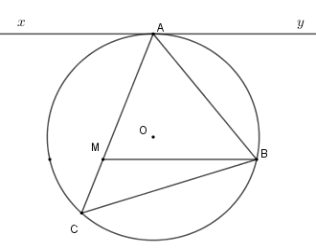
Ta có \(\widehat {yAB} = \widehat {ACB}\) (hệ quả) mà \(\widehat {yAB} = \widehat {ABM}\) (so le trong) nên \(\widehat {ACB} = \widehat {ABM} \Rightarrow \Delta AMB\backsim\Delta ABC\left( {g - g} \right)\)
\(\dfrac{{AM}}{{AB}} = \dfrac{{AB}}{{AC}} \Rightarrow AM.AC = A{B^2}\) .