Đề kiểm tra 15 phút chương 8: Hình trụ - Hình nón - Hình cầu - Đề số 1 — Không quảng cáo

Sử dụng công thức tính diện tích toàn phần của hình trụ ${S_{tp}} = {S_{xq}} + {S_{2d}} = 2\pi Rh + 2\pi {R^2}$ để tính bán kính đáy

Diện tích toàn phần của hình trụ là:

${S_{tp}} = {S_{xq}} + {S_{2d}} = 2\pi Rh + 2\pi {R^2} = 564\pi $

Suy ra \(16\pi h + 2\pi {.8^2} = 564\pi\)

Do đó \(h = 27,25\,(cm)\)

Sử dụng diện tích đáy ${S_{_d}} = \pi {R^2}$ để tính bán kính \(R\) .

Sử dụng công thức tính diện tích xung quanh của hình trụ ${S_{xq}} = 2\pi Rh$

Bán kính \(R\) của đường tròn đáy là \(\pi {R^2} = 25\pi \) suy ra \( R = 5\,cm\)

Diện tích xung quanh của hình trụ là:

\({S_{xq}} = 2\pi Rh = 2\pi .5.10 = 100\pi \left( {c{m^2}} \right)\)

Vì trục lăn \(12\) vòng nên diện tích tạo trên sân phẳng là \(12.100\pi  = 1200\pi \,\left( {c{m^2}} \right)\)

Sử dụng công thức liên hệ \({R^2} + {h^2} = {l^2}\) để tính đường sinh

Sử dụng công thức tính diện tích xung quanh của hình nón \({S_{xq}} = \pi Rl\)

Vì \({R^2} + {h^2} = {l^2}\) hay \({3^2} + {4^2} = {l^2}\)

nên \({l^2} = 25\) suy ra \(l = 5\,cm\)

Diện tích xung quanh của hình trụ là:

\({S_{xq}} = \pi Rl = \pi .3.5 = 15\pi \,\,\left( {c{m^2}} \right)\)

Sử dụng công thức tính diện tích xung quanh của hình nón \({S_{xq}} = \pi Rl\) để tính đường sinh.

Sử dụng công thức liên hệ \({R^2} + {h^2} = {l^2}\) để tìm chiều cao hình nón

Sử dụng công thức thể tich khối nón \(V = \dfrac{1}{3}\pi {R^2}h.\)

Bán kính đường tròn đáy là:

\(R = \dfrac{d}{2} = \dfrac{{10}}{2} = 5\,cm\)

Diện tích xung quanh là:

\({S_{xq}} = \pi Rl = \pi .5.l = 65\pi  \)

Suy ra \(l = 13\,cm\)

Ta có \({R^2} + {h^2} = {l^2}\)

\({5^2} + {h^2} = {13^2}\)

\({h^2} = 144\)

Suy ra \( h = 12\,cm\)

Thể tích khối nón là:

\(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {.5^2}.12 \)

\(= 100\pi \,\left( {c{m^3}} \right)\)

Sử dụng công thức tính chu vi đường tròn \(C = 2\pi R\) để tính bán kính đáy

Sử dụng công thức tính thể tích hình trụ bán kính \(R\) và chiều cao \(h\): \(V = \pi {R^2}h\)

Ta có chu vi đáy \(C = 2\pi R = 8\pi\) suy ra \(R = 4\)

Thể tích hình trụ là \(V = \pi {R^2}h = \pi {.4^2}.10 = 160\pi \) (đvtt).

Sử dụng công thức liên hệ \({R^2} + {h^2} = {l^2}\)

Sử dụng công thức tính diện tích xung quanh của hình nón \({S_{xq}} = \pi Rl\) .

Ta có đường sinh mới là: \({l'^2} = {\left( {2R} \right)^2} + {\left( {2h} \right)^2} = 4\left( {{R^2} + {h^2}} \right) = {\left( {2l} \right)^2} \)

Suy ra \(l' = 2l\)

Khi đó diện tích xung quanh mới là:

\({S'_{xq}} = \pi .\left( {2R} \right).\left( {2l} \right) = 4.\pi Rl = 4{S_{xq}}\) .

Vậy diện tích xung quanh của hình nón tăng \(4\) lần.

Sử dụng công thức diện tích xung quanh của hình trụ ${S_{xq}} = 2\pi Rh$ và công thức diện tích toàn phần \({S_{tp}} = 2\pi Rh + 2\pi {R^2}\)

Từ giả thiết ta cóL

\(2\pi Rh + 2\pi {R^2} = 2.2.\pi Rh\)

\(Rh = {R^2}\)

\(R = h\) . Vậy chiều cao của hình trụ là $3\,cm$ .

Sử dụng công thức tính diện tích toàn phần của hình nón \({S_{tp}} = \pi Rl + \pi {R^2}\) .

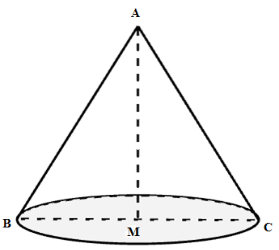
Xét tam giác \(ABC\) đều có \(AM\) vừa là đường trung tuyến, đường cao, đường phân giác.

Nên ta có \(MC = \dfrac{{BC}}{2} = \dfrac{a}{2}\) .

Khi quay tam giác $ABC$ quanh cạnh \(AM\) ta được hình nón đỉnh \(A\) , bán kính đáy là \(MC\) , đường sinh \(AC\) và chiều cao \(AM\) .

Diện tích toàn phần của hình nón là \({S_{tp}} = \pi Rl + \pi {R^2} = \pi .MC.AC + \pi .M{C^2} = \pi .\dfrac{a}{2}.a + \pi .{\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{3\pi {a^2}}}{4}\) .