Đề kiểm tra 15 phút chương 6: Đường tròn - Đề số 1 — Không quảng cáo

Sử dụng nhận xét: “ Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp” từ đó suy ra bán kính của đường tròn ngoại tiếp.

Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp. Do đó bán kính đường tròn ngoại tiếp tam giác vuông bằng nửa cạnh huyền.

Đường tròn là hình có trục đối xứng. Bất kỳ đường kính nào cũng là trục đối xứng của đường tròn

Nên đường tròn có vô số trục đối xứng.

Trong các dây của đường tròn, dây lớn nhất là đường kính.

- Trong một đường tròn:  Dây nào gần tâm hơn thì dây đó lớn hơn.

Từ đề bài ta thấy dây $CD$ gần tâm hơn dây $AB$ nên $CD > AB.$

Sử dụng kiến thức “Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy”, sau đó dùng định lý Pytago vào tam giác vuông thích hợp.

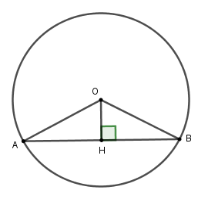
Kẻ $OH \bot AB$ tại $H$ suy ra $H$ là trung điểm của $AB$.

Xét tam giác $OHB$ vuông tại $H$ có $OH = 3;OB = 5$. Theo định lý Pytago ta có $HB = \sqrt {O{B^2} - O{H^2}}  = \sqrt {{5^2} - {3^2}}  = 4$

Mà $H$ là trung điểm của $AB$ nên $AB = 2HB = 8\,cm$

Vậy $AB = 8\,cm$.

+ Tính khoảng cách theo công thức $AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}}$ với $A\left( {{x_A};{y_A}} \right);B\left( {{x_B};{y_B}} \right)$

+ Sử dụng vị trí tương đối  giữa điểm và đường tròn

Cho điểm $M$  và đường tròn $\left( {O;R} \right)$ ta so sánh khoảng cách $OM$ với bán kính R để xác định vị trí tương đối theo bảng sau:

Ta có $OA = \sqrt {{{\left( { - 1 - 0} \right)}^2} + {{\left( { - 1 - 0} \right)}^2}}  = \sqrt 2  < 2 = R$ nên $A$ nằm trong đường tròn tâm $O$ bán kính $R = 2$.

Kẻ các đường vuông góc từ tâm đến dây.

Sử dụng mối liên hệ giữa dây và đường kính và tính chất hình chữ nhật để suy ra khoảng cách.

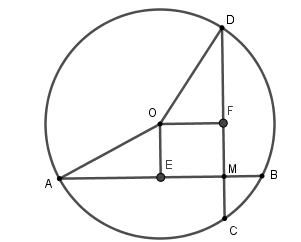
Xét đường tròn tâm $\left( O \right)$,

Kẻ $OE \bot AB$ tại $E$ suy ra $E$ là trung điểm của $AB$, kẻ $OF \bot CD$ tại $F$ suy ra $F$ là trung điểm của $CD$,

Xét tứ giác $OEMF$ có $\widehat E = \widehat F = \widehat M = 90^\circ$ nên $OEIF$ là hình chữ nhật, suy ra $FM = OE$.

Ta có $CD = 8\,cm \Rightarrow FC = 4\,cm$ mà $MC = 1\,cm \Rightarrow FM = FC - MC = 4 - 1 = 3\,cm$ nên $OE = FM = \,3cm$

Vậy khoảng cách từ tâm $O$ đến dây $AB$ là $3\,cm$

Sử dụng kiến  thức “Hai dây bằng nhau thì cách đều tâm”  và tính chất hình vuông

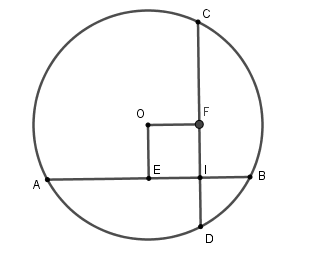
Xét đường tròn tâm $\left( O \right)$,

Kẻ $OE \bot AB$ tại $E$ suy ra $E$ là trung điểm của $AB$, kẻ $OF \bot CD$ tại $F$.

Vì dây $AB = CD$ nên $OE = OF$ (hai dây bằng nhau cách đều tâm)

Xét tứ giác $OEIF$ có $\widehat E = \widehat F = \widehat I = 90^\circ$ nên $OEIF$ là hình chữ nhật và $OE = OF$ nên $OEIF$ là hình vuông$\Rightarrow OE = OF = EI$

Mà $AB = IA + IB = 9\,cm$ $\Rightarrow EB = 4,5\,cm \Rightarrow EI = EB - IB = 1,5\,cm$ nên $OE = OF = 1,5\,cm$

Vậy tổng khoảng cách từ tâm đến hai dây $AB,CD$ là $1,5 + 1,5 = 3\,cm$.

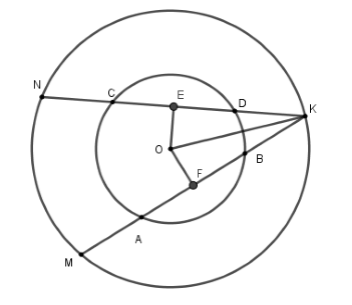
Xét đường tròn $\left( {O;OB} \right)$

Kẻ $OE \bot CD;OF \bot AB$ tại $E,F$ mà $CD = AB \Rightarrow OE = OF$ (hai dây bằng nhau thì cách đều tâm)

Xét đường tròn $\left( {O;OK} \right)$ có $OE \bot KN;OF \bot KM$ tại $E,F$ mà $OE = OF \Rightarrow KN = KM$( liên hệ giữa dây và khoảng cách từ tâm đến dây)

Kẻ các đường vuông góc từ tâm đến dây. Sử dụng mối liên hệ giữa dây và đường kính và tính chất hình chữ nhật để suy ra khoảng cách.

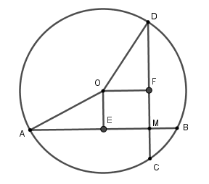
Lấy $E$; $F$ lần lượt là trung điểm của hai dây $AB$ và $CD$. Khi đó

$OE \bot AB;\,OF \bot AC$ lại có $\widehat {FME} = 90^\circ$ nên $OEMF$ là hình chữ nhật. Suy ra $OE=MF=CF-MC=4 \,\ cm.$

Xét đường tròn tâm $\left( O \right)$,

Có $OE = \,4\,cm$, $E$ là trung điểm của $AB$ nên $AE = \dfrac{{14}}{2} = 7cm$

Áp dụng định lý Pytago cho tam giác vuông $OEA$ ta có $OA = \sqrt {A{E^2} + O{E^2}}  = \sqrt {65}$ nên $R = \sqrt {65}$

Lại có $OD = \sqrt {65} \,\ cm ;FD = 6 \,\ cm$ nên áp dụng định lý Pytago cho tam giác vuông $OFD$ ta có

$OF = \sqrt {O{D^2} - F{D^2}}  = \sqrt {29} \,\ cm$. Do đó khoảng cách từ tâm đến dây $CD$ là $\sqrt {29}$$cm$ .