Đề kiểm tra 15 phút chương 5: Hệ thức lượng trong tam giác vuông - Đề số 1
Đề bài
Không dùng bảng số và máy tính, hãy so sánh \(\sin 20^\circ \) và \(\sin 70^\circ \)
-
A.
$\sin 20^\circ < \sin 70^\circ $
-
B.
$\sin 20^\circ > \sin 70^\circ $
-
C.
$\sin 20^\circ = \sin 70^\circ $
-
D.
$\sin 20^\circ \ge \sin 70^\circ $
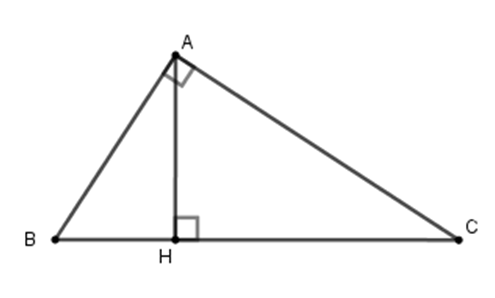
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là sai?
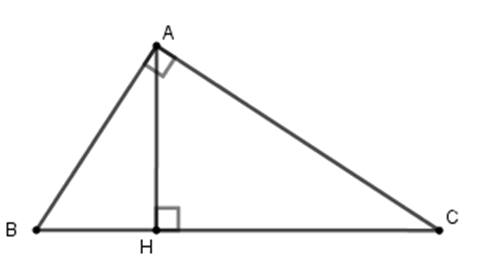
-
A.
$A{B^2} = BH.BC$
-
B.
$A{C^2} = CH.BC$
-
C.
$AB.AC = AH.BC$
-
D.
$A{H^2} = \dfrac{{A{B^2} + A{C^2}}}{{A{B^2}.A{C^2}}}$
Cho tam giác $ABC$ vuông tại $A$ có \(BC = 8\,cm,\,\,AC = 6cm.\) Tính tỉ số lượng giác $\tan C$ (làm tròn đến chữ số thập phân thứ $2$ ).
-
A.
$\tan C \approx 0,87$
-
B.
$\tan C \approx 0,86$
-
C.
$\tan C \approx 0,88$
-
D.
$\tan C \approx 0,89$
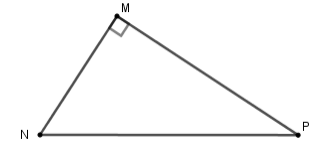
Cho tam giác \(MNP\) vuông tại \(M\). Khi đó \(\tan \widehat {MNP}\) bằng
-
A.
\(\dfrac{{MN}}{{NP}}\)
-
B.
\(\dfrac{{MP}}{{NP}}\)
-
C.
\(\dfrac{{MN}}{{MP}}\)
-
D.
\(\dfrac{{MP}}{{MN}}\)
Tính $x$ trong hình vẽ sau (làm tròn đến chữ số thập phân thứ hai)
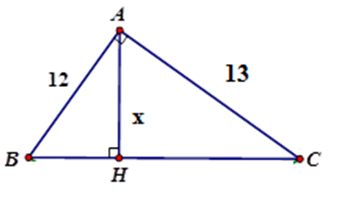
-
A.
$x \approx 8,81$
-
B.
$x \approx 8,82$
-
C.
$x \approx 8,83$
-
D.
$x \approx 8,80$
Cho tam giác $ABC$ vuông tại $A$ , $AH \bot BC$ ( $H$ thuộc $BC$ ). Cho biết $AB:AC = 3:4$ và $BC = 15cm.$ Tính độ dài đoạn thẳng $BH$ .
-
A.
$BH = 5,4$
-
B.
$BH = 4,4$
-
C.
$BH = 5,2$
-
D.
$BH = 5$
Tính $x,y$ trong hình vẽ sau:
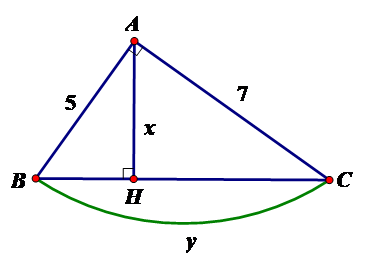
-
A.
$x = \dfrac{{35\sqrt {74} }}{{74}};y = \sqrt {74} $
-
B.
$y = \dfrac{{35\sqrt {74} }}{{74}};x= \sqrt {74} $
-
C.
$x = 4;y = 6$
-
D.
$x = 2,8;y = 7,2$
Tính $x,y$ trong hình vẽ sau:
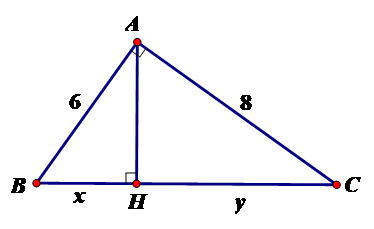
-
A.
$x = 3,6;y = 6,4$
-
B.
$y = 3,6;x = 6,4$
-
C.
$x = 4;y = 6$
-
D.
$x = 2,8;y = 7,2$
Tính giá trị biểu thức $B = \tan 1^\circ .\tan 2^\circ .\tan 3^\circ .....\tan88^\circ .\tan89^\circ $
-
A.
$B = 44$
-
B.
$B = 1$
-
C.
$B = 45$
-
D.
$B = 2$
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(AB = 13\,cm,\,BH = 0,5\,dm\) Tính tỉ số lượng giác $\sin C$ (làm tròn đến chữ số thập phân thứ $2$ )
-
A.
$\sin C \approx 0,35$
-
B.
$\sin C \approx 0,37$
-
C.
$\sin C \approx 0,39$
-
D.
$\sin C \approx 0,38$
Lời giải và đáp án
Không dùng bảng số và máy tính, hãy so sánh \(\sin 20^\circ \) và \(\sin 70^\circ \)
-
A.
$\sin 20^\circ < \sin 70^\circ $
-
B.
$\sin 20^\circ > \sin 70^\circ $
-
C.
$\sin 20^\circ = \sin 70^\circ $
-
D.
$\sin 20^\circ \ge \sin 70^\circ $
Đáp án : A
Sử dụng nhận xét : Với góc nhọn \(\alpha ,\,\beta ,\) ta có: $\sin \alpha < \sin \beta \Leftrightarrow \alpha < \beta $
Vì $20^\circ < 70^\circ \Leftrightarrow \sin 20^\circ < \sin 70^\circ $.
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là sai?

-
A.
$A{B^2} = BH.BC$
-
B.
$A{C^2} = CH.BC$
-
C.
$AB.AC = AH.BC$
-
D.
$A{H^2} = \dfrac{{A{B^2} + A{C^2}}}{{A{B^2}.A{C^2}}}$
Đáp án : D
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ . Khi đó ta có các hệ thức
$A{C^2} = CH.BC$ ; $A{B^2} = BH.BC$ ; $AB.AC = BC.AH$ và $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
Nhận thấy phương án D: $A{H^2} = \dfrac{{A{B^2} + A{C^2}}}{{A{B^2}.A{C^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$ là sai.
Cho tam giác $ABC$ vuông tại $A$ có \(BC = 8\,cm,\,\,AC = 6cm.\) Tính tỉ số lượng giác $\tan C$ (làm tròn đến chữ số thập phân thứ $2$ ).
-
A.
$\tan C \approx 0,87$
-
B.
$\tan C \approx 0,86$
-
C.
$\tan C \approx 0,88$
-
D.
$\tan C \approx 0,89$
Đáp án : C
Bước 1: Tính cạnh còn lại theo định lý Pytago
Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn
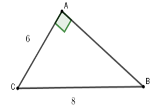
Theo định lý Py-ta-go ta có: $B{C^2} = A{C^2} + A{B^2} \Rightarrow AB = \sqrt {{8^2} - {6^2}} \approx 5,29$
Xét tam giác $ABC$ vuông tại $C$ có $\tan C = \dfrac{{AB}}{{AC}} \approx \dfrac{{5,29}}{6} \approx 0,88.$

Cho tam giác \(MNP\) vuông tại \(M\). Khi đó \(\tan \widehat {MNP}\) bằng
-
A.
\(\dfrac{{MN}}{{NP}}\)
-
B.
\(\dfrac{{MP}}{{NP}}\)
-
C.
\(\dfrac{{MN}}{{MP}}\)
-
D.
\(\dfrac{{MP}}{{MN}}\)
Đáp án : D
Ta có \(\tan \widehat {MNP} = \dfrac{{MP}}{{MN}}\)
Tính $x$ trong hình vẽ sau (làm tròn đến chữ số thập phân thứ hai)

-
A.
$x \approx 8,81$
-
B.
$x \approx 8,82$
-
C.
$x \approx 8,83$
-
D.
$x \approx 8,80$
Đáp án : B
Tính $x$ theo hệ thức lượng $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
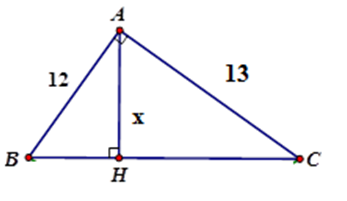
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông $ABC$ ta có:
$\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
\( \Leftrightarrow \dfrac{1}{{A{H^2}}} = \dfrac{{A{B^2} + A{C^2}}}{{A{B^2}.A{C^2}}} \)\(\Leftrightarrow A{H^2} = \dfrac{{A{B^2}.A{C^2}}}{{A{B^2} + A{C^2} }}\)
$ \Rightarrow AH = \dfrac{{AB.AC}}{{\sqrt {A{B^2} + A{C^2}} }} = \dfrac{{12.13}}{{\sqrt {{{12}^2} + {{13}^2}} }} \approx 8,82$
Vậy $x \approx 8,82$ .
Cho tam giác $ABC$ vuông tại $A$ , $AH \bot BC$ ( $H$ thuộc $BC$ ). Cho biết $AB:AC = 3:4$ và $BC = 15cm.$ Tính độ dài đoạn thẳng $BH$ .
-
A.
$BH = 5,4$
-
B.
$BH = 4,4$
-
C.
$BH = 5,2$
-
D.
$BH = 5$
Đáp án : A
Bước 1: Sử dụng tính chất dãy tỉ số bằng nhau để tìm $AB,AC$ . $\left( {\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a + c}}{{b + d}}} \right)$
Bước 2: Tính $BH$ theo hệ thức $A{B^2} = BH.BC$
Ta có $AB:AC = 3:4$$ \Leftrightarrow \dfrac{{AB}}{3} = \dfrac{{AC}}{4} \Rightarrow \dfrac{{A{B^2}}}{9} = \dfrac{{A{C^2}}}{{16}} $$= \dfrac{{A{B^2} + A{C^2}}}{{9+16}}= \dfrac{{A{B^2} + A{C^2}}}{{25}}$ $=\dfrac{{B{C^2}}}{{25}}$$= \dfrac{{225}}{{25}} = 9$
(Vì theo định lý Pytago ta có $A{B^2} + A{C^2} = B{C^2} \Leftrightarrow A{B^2} + A{C^2} = 225$ )
Nên $\dfrac{{A{B^2}}}{9} = 9 \Rightarrow AB = 9$ ; $\dfrac{{A{C^2}}}{{16}} = 9 \Rightarrow AC = 12$
Theo hệ thức lượng trong tam giác vuông $ABC$ ta có $A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{81}}{{15}} = 5,4$
Vậy $BH = 5,4$ .
Tính $x,y$ trong hình vẽ sau:

-
A.
$x = \dfrac{{35\sqrt {74} }}{{74}};y = \sqrt {74} $
-
B.
$y = \dfrac{{35\sqrt {74} }}{{74}};x= \sqrt {74} $
-
C.
$x = 4;y = 6$
-
D.
$x = 2,8;y = 7,2$
Đáp án : A
Bước 1: Tính $BC$ theo định lý Pytago
Bước 2: Tính $x,y$ theo hệ thức lượng $AH.BC = AB.AC$
Theo định lý Pytago ta có $B{C^2} = A{B^2} + A{C^2} \Leftrightarrow B{C^2} = 74 \Leftrightarrow BC = \sqrt {74} $
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$AH.BC = AB.AC \Leftrightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{5.7}}{{\sqrt {74} }} = \dfrac{{35\sqrt {74} }}{{74}}$
Vậy $x = \dfrac{{35\sqrt {74} }}{{74}};y = \sqrt {74} $
Tính $x,y$ trong hình vẽ sau:

-
A.
$x = 3,6;y = 6,4$
-
B.
$y = 3,6;x = 6,4$
-
C.
$x = 4;y = 6$
-
D.
$x = 2,8;y = 7,2$
Đáp án : A
Bước 1: Tính $BC$ theo định lý Pytago
Bước 2: Tính $x,y$ theo hệ thức lượng $A{B^2} = BH.BC;A{C^2} = CH.BC$
Theo định lý Pytago ta có $B{C^2} = A{B^2} + A{C^2} \Leftrightarrow B{C^2} = 100 \Leftrightarrow BC = 10$
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} $
$= \dfrac{{{6^2}}}{10} = 3,6$ hay $x = 3,6$
$ \Rightarrow CH = BC - BH $$= 10 - 3,6 = 6,4.$
hay $y = 6,4$ .
Vậy $x = 3,6;y = 6,4.$
Tính giá trị biểu thức $B = \tan 1^\circ .\tan 2^\circ .\tan 3^\circ .....\tan88^\circ .\tan89^\circ $
-
A.
$B = 44$
-
B.
$B = 1$
-
C.
$B = 45$
-
D.
$B = 2$
Đáp án : B
Bước 1 : Đưa các tỉ số lượng giác về cùng một góc hoặc cùng loại (sử dụng tính chất "Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia")
Bước 2 : Sử dụng đẳng thức lượng giác $\tan \alpha .\cot\alpha = 1$.
Ta có $\tan 89^\circ = \cot1^\circ ;\tan 88^\circ = \cot2^\circ ;..;\tan 46^\circ = \cot44^\circ $ và $\tan \alpha .\cot\alpha = 1$
Nên $B = \left( {\tan 1^\circ .\tan 89^\circ } \right).\left( {\tan 2^\circ .\tan 88^\circ } \right)....\left( {\tan 46^\circ .\tan 44^\circ } \right).\tan 45^\circ $
$ = \left( {\tan 1^\circ .\cot 1^\circ } \right).\left( {\tan 2^\circ .\cot 2^\circ } \right).\left( {\tan 3^\circ .\cot 3^\circ } \right)....\left( {\tan 44^\circ .\cot 44^\circ } \right).\tan 45^\circ $
$ = 1.1.1....1.1 = 1$
Vậy $B = 1$.
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(AB = 13\,cm,\,BH = 0,5\,dm\) Tính tỉ số lượng giác $\sin C$ (làm tròn đến chữ số thập phân thứ $2$ )
-
A.
$\sin C \approx 0,35$
-
B.
$\sin C \approx 0,37$
-
C.
$\sin C \approx 0,39$
-
D.
$\sin C \approx 0,38$
Đáp án : D
Bước 1: Tính cạnh cần thiết lại theo định lý Pytago hoặc hệ thức lượng trong tam giác vuông.
Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn
Đổi $0,5\,dm = 5\,cm$
Xét tam giác $ABC$ vuông tại $A$,
theo hệ thức lượng trong tam giác vuông ta có
$A{B^2} = BH.BC \Rightarrow BC = \dfrac{{A{B^2}}}{{BH}} = \dfrac{{{{13}^2}}}{5} = 33,8\,\,cm$
$ \Rightarrow \sin C = \dfrac{{AB}}{{BC}}$
$= \dfrac{{13}}{{33,8}} \approx 0,38$