Đề kiểm tra 15 phút chương 7: Góc với đường tròn - Đề số 2
Đề bài
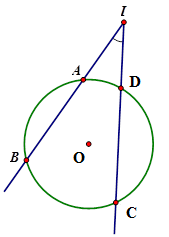
Cho hình vẽ dưới đây, góc \(BIC\) có số đo bằng
-
A.
$\dfrac{1}{2}$(sđ \(\overparen{BC} + \) sđ \(\overparen{AD}\) )
-
B.
$\dfrac{1}{2}$(sđ \(\overparen{BC} - \) sđ \(\overparen{AD}\) )
-
C.
$\dfrac{1}{2}$(sđ \(\overparen{AB} + \) sđ \(\overparen{CD}\) )
-
D.
$\dfrac{1}{2}$(sđ \(\overparen{AB} - \) sđ \(\overparen{CD}\) )
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) và \(C\) là điểm trên cung nhỏ \(AB\) (cung \(CB\) nhỏ hơn cung \(CA\) ). Tiếp tuyến tại \(C\) của nửa đường tròn cắt đường thẳng \(AB\) tại \(D\) . Biết tam giác \(ADC\) cân tại \(C\) . Tính góc \(ADC\) .
-
A.
$40^\circ $
-
B.
$45^\circ $
-
C.
$60^\circ $
-
D.
$30^\circ $
Cho \(\Delta ABC\) cân tại \(A\) có \(\widehat {BAC} = {120^0}.\) Trên nửa mặt phẳng bờ \(BC\) không chứa đỉnh \(A\), lấy \(D\) sao cho \(BCD\) là tam giác đều. Khi đó
-
A.
\(\Delta ACD\) cân
-
B.
\(ABDC\) nội tiếp
-
C.
\(ABDC\) là hình thang
-
D.
\(ABDC\) là hình vuông
Đường tròn ngoại tiếp đa giác là đường tròn
-
A.
Tiếp xúc với tất cả các cạnh của đa giác đó
-
B.
Đi qua tất cả các đỉnh của đa giác đó
-
C.
Cắt tất cả các cạnh của đa giác đó
-
D.
Đi qua tâm của đa giác đó
Tính cạnh của hình vuông nội tiếp \(\left( {O;R} \right)\)
-
A.
\(\dfrac{R}{{\sqrt 2 }}\)
-
B.
\(2R\)
-
C.
\(\sqrt 2 R\)
-
D.
\(2\sqrt 2 R\)
Trên \(\left( O \right)\) lấy bốn điểm \(A,B,C,D\) theo thứ tự sao cho cung \(AB = \) cung \(BC = \) cung \(CD\) . Gọi \(I\) là giao điểm của \(BD\) và \(AC\) , biết \(\widehat {BIC} = 70^\circ \) . Tính \(\widehat {ABD}\) .
-
A.
$20^\circ $
-
B.
$15^\circ $
-
C.
$35^\circ $
-
D.
$30^\circ $
Cho \(\Delta ABC\) vuông ở $A$ . Trên cạnh $AC$ lấy điểm $M$ và vẽ đường tròn đường kính $MC$ . Kẻ $BM$ cắt đường tròn tại $D$ . Đường thẳng $DA$ cắt đường tròn tại $S$ . Chọn đáp án sai trong các đáp án sau:
-
A.
Tứ giác $ABCD$ nội tiếp.
-
B.
\(\widehat {ABD} = \widehat {ACD}\)
-
C.
$CA$ là phân giác của \(\widehat {SCB}.\)
-
D.
Tứ giác $ABCS$ nội tiếp.
Cho tam giác $ABC$ vuông tại $A$ và điểm $D$ nằm giữa $A$ và $B$ . Đường tròn đường kính $BD$ cắt $BC$ tại $E$. Các đường thẳng $CD$ , $AE$ lần lượt cắt đường tròn tại các điểm thứ hai là $F$ và $G$. Khi đó, kết luận không đúng là:
-
A.
$\Delta ABC\backsim\Delta EBD$.
-
B.
Tứ giác $ADEC$ là tứ giác nội tiếp.
-
C.
Tứ giác $AFBC$ không là tứ giác nội tiếp.
-
D.
Các đường thẳng $AC,DE$ và $BF$ đồng quy.
Lời giải và đáp án
Cho hình vẽ dưới đây, góc \(BIC\) có số đo bằng

-
A.
$\dfrac{1}{2}$(sđ \(\overparen{BC} + \) sđ \(\overparen{AD}\) )
-
B.
$\dfrac{1}{2}$(sđ \(\overparen{BC} - \) sđ \(\overparen{AD}\) )
-
C.
$\dfrac{1}{2}$(sđ \(\overparen{AB} + \) sđ \(\overparen{CD}\) )
-
D.
$\dfrac{1}{2}$(sđ \(\overparen{AB} - \) sđ \(\overparen{CD}\) )
Đáp án : B
Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
\(\widehat {BIC} = \)$\dfrac{1}{2}$(sđ \(\overparen{BC} - \) sđ \(\overparen{AD}\) )
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) và \(C\) là điểm trên cung nhỏ \(AB\) (cung \(CB\) nhỏ hơn cung \(CA\) ). Tiếp tuyến tại \(C\) của nửa đường tròn cắt đường thẳng \(AB\) tại \(D\) . Biết tam giác \(ADC\) cân tại \(C\) . Tính góc \(ADC\) .
-
A.
$40^\circ $
-
B.
$45^\circ $
-
C.
$60^\circ $
-
D.
$30^\circ $
Đáp án : D
Sử dụng góc nội tiếp và góc có đỉnh bên ngoài đường tròn
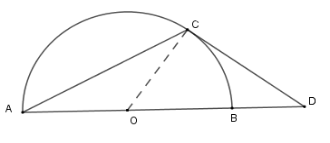
Xét nửa \(\left( O \right)\) có \(\widehat {BAC} = \dfrac{1}{2}\) sđ \(\overparen{BC}\) (góc nội tiếp chắn cung BC) và \(\widehat {CDA} = \dfrac{1}{2}\) (sđ \(\overparen{AC} - \) sđ \(\overparen{BC}\) ) (góc có đỉnh bên ngoài đường tròn)
Mà \(\Delta ADC\) cân tại \(C\) nên \(\widehat {DAC} = \widehat {CDA} \Leftrightarrow \) sđ \(\overparen{BC} = \) sđ \(\overparen{AC} - \) sđ \(\overparen{BC}\)
Suy ra sđ \(\overparen{AC} = 2\). sđ \(\overparen{BC}\)
Mà sđ \(\overparen{AC} + \) sđ \(\overparen{BC} = 180^\circ \) nên sđ \(\overparen{AC} = 120^\circ \) ; sđ\(\overparen{BC}= 60^\circ \)
Do đó $\widehat {ADC} = 30^\circ $.
Cho \(\Delta ABC\) cân tại \(A\) có \(\widehat {BAC} = {120^0}.\) Trên nửa mặt phẳng bờ \(BC\) không chứa đỉnh \(A\), lấy \(D\) sao cho \(BCD\) là tam giác đều. Khi đó
-
A.
\(\Delta ACD\) cân
-
B.
\(ABDC\) nội tiếp
-
C.
\(ABDC\) là hình thang
-
D.
\(ABDC\) là hình vuông
Đáp án : B
Chứng minh tam giác ABD và tam giác ACD là hai tam giác vuông nội tiếp đường tròn đường kính AD nên là tứ giác nội tiếp.
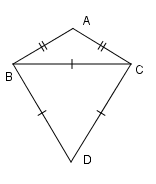
Ta có $\Delta BCD$ là tam giác đều nên \(\widehat {DCB} = {60^0}\,\,\left( 1 \right).\)
Mặt khác \(\Delta ABC\) là tam giác cân tại \(A\) có $\widehat {BAC} = {120^0}$. Áp dụng định lí tổng ba góc trong một tam giác bằng \({180^0}\) nên \(\widehat {ACB} = \widehat {ABC}\) và \(\widehat {ACB} + \widehat {ABC} + \widehat {BAC} = {180^0}\) nên \(\widehat {ACB} = {30^0}\,\,\,\,\left( 2 \right)\) .
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có \(\widehat {ACD} = \widehat {DCB} + \widehat {BCA} = {60^0} + {30^0} = {90^0}\).
Tam giác ACD có \(\widehat {ACD} = {90^0}\) nên nội tiếp đường tròn đường kính AD. (3)
Chứng minh tương tự ta có \(\widehat {ABD} = {90^0}\).
Tam giác ABD có \(\widehat {ABD} = {90^0}\) nên nội tiếp đường tròn đường kính AD. (4)
Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) suy ra tứ giác \(ABDC\) là tứ giác nội tiếp (vì bốn đỉnh A, B, C, D cùng thuộc đường tròn đường kính AD).
Đường tròn ngoại tiếp đa giác là đường tròn
-
A.
Tiếp xúc với tất cả các cạnh của đa giác đó
-
B.
Đi qua tất cả các đỉnh của đa giác đó
-
C.
Cắt tất cả các cạnh của đa giác đó
-
D.
Đi qua tâm của đa giác đó
Đáp án : B
Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác .
Tính cạnh của hình vuông nội tiếp \(\left( {O;R} \right)\)
-
A.
\(\dfrac{R}{{\sqrt 2 }}\)
-
B.
\(2R\)
-
C.
\(\sqrt 2 R\)
-
D.
\(2\sqrt 2 R\)
Đáp án : C
+ Sử dụng tính chất hình vuông để tìm bán kính đường tròn
+ Sử dụng định lý Pythagore để tìm cạnh của hình vuông
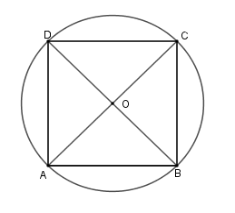
Gọi \(ABCD\) là hình vuông cạnh \(a\) nội tiếp đường tròn \(\left( O \right)\) suy ra $O$ là giao điểm hai đường chéo \(AC\) và \(BD\)
Từ đó \(R = OA = \dfrac{{AC}}{2}\) suy ra \(AC = 2R\)
Áp dụng định lý Pythagore vào tam giác ABC ta có \(A{B^2} + B{C^2} = A{C^2} \) suy ra \(A{C^2} = {a^2} + {a^2} = 2{a^2}\)
Do đó \( AC = a\sqrt 2 = 2R\), suy ra \(a = \sqrt 2 R\).
Trên \(\left( O \right)\) lấy bốn điểm \(A,B,C,D\) theo thứ tự sao cho cung \(AB = \) cung \(BC = \) cung \(CD\) . Gọi \(I\) là giao điểm của \(BD\) và \(AC\) , biết \(\widehat {BIC} = 70^\circ \) . Tính \(\widehat {ABD}\) .
-
A.
$20^\circ $
-
B.
$15^\circ $
-
C.
$35^\circ $
-
D.
$30^\circ $
Đáp án : B
Sử dụng góc nội tiếp và góc có đỉnh bên trong đường tròn
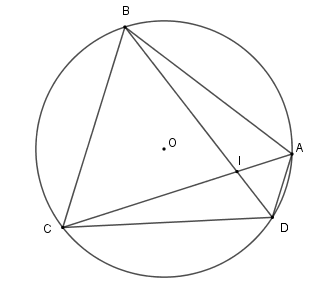
Vì cung \(AB = \) cung \(BC = \) cung \(CD\) nên gọi số đo mỗi cung là $a$ độ. Ta có số đo cung \(AD\) là \(360^\circ - 3a\)
Vì \(\widehat {BIC}\) là góc có đỉnh bên trong đường tròn nên
$\widehat {BIC} = \dfrac{{a + 360^\circ - 3a}}{2} = 70^\circ \Rightarrow a = 110^\circ \Rightarrow $ số đo cung \(AD\) là $360^\circ - 3.110^\circ = 30^\circ $
\(\widehat {ABD}\) là góc nội tiếp chắn cung \(AD\) nên \(\widehat {ABD} = \dfrac{{30^\circ }}{2} = 15^\circ \) .
Cho \(\Delta ABC\) vuông ở $A$ . Trên cạnh $AC$ lấy điểm $M$ và vẽ đường tròn đường kính $MC$ . Kẻ $BM$ cắt đường tròn tại $D$ . Đường thẳng $DA$ cắt đường tròn tại $S$ . Chọn đáp án sai trong các đáp án sau:
-
A.
Tứ giác $ABCD$ nội tiếp.
-
B.
\(\widehat {ABD} = \widehat {ACD}\)
-
C.
$CA$ là phân giác của \(\widehat {SCB}.\)
-
D.
Tứ giác $ABCS$ nội tiếp.
Đáp án : D
Góc nội tiếp chắn nửa đường tròn là góc vuông.
Dấu hiệu nhận biết tứ giác nội tiếp:
+) Tứ giác có tổng hai góc đối diện bằng \({180^0}.\)
+) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\)
+) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác.
+) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.
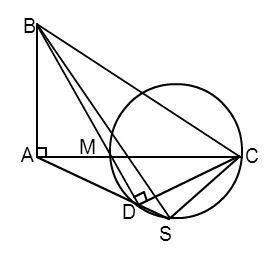
+) Ta có: \(\widehat {MDC}\) là góc nội tiếp chắn nửa đường tròn đường kính $MC$ \( \Rightarrow \widehat {MDC} = {90^0}\) (tính chất góc nội tiếp).
Xét tứ giác $ABCD$ ta có:
Góc $BAC$ và góc $BDC$ cùng nhìn đoạn $BC$ dưới góc \({90^0}.\)
\( \Rightarrow \) $ABCD$ là tứ giác nội tiếp (dhnb) \( \Rightarrow \) phương án A đúng.
+) Xét tứ giác $ABCD$ nội tiếp ta có\(\widehat {ABD} = \widehat {ACD}\) (cùng nhìn đoạn $AD$ )\( \Rightarrow \) phương án B đúng.
+) Xét đường tròn đường kính $MC$ ta có $4$ điểm $M,C,D,S$ cùng thuộc đường tròn.
\( \Rightarrow \) Tứ giác $MCSD$ là tứ giác nội tiếp.
\( \Rightarrow \widehat {ADM} = \widehat {SCM}\) (góc ngoài tại $1$ đỉnh bằng góc trong tại đỉnh đối diện). $\left( 1 \right)$
Vì tứ giác $ABCD$ nội tiếp (cmt) \( \Rightarrow \widehat {ACB} = \widehat {ADB}\) (cùng nhìn đoạn$AB$ ) $\left( 2 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)$ \( \Rightarrow \widehat {BCA} = \widehat {ACS}\;\;\;\left( { = \widehat {ADB}} \right).\)
Hay $CA$ là phân giác của \(\widehat {SCB} \Rightarrow \) phương án C đúng.
+) Giả sử tứ giác $ABCS$ là tứ giác nội tiếp \( \Rightarrow \widehat {ASB} = \widehat {BCA}\) (hai góc cùng nhìn đoạn $AB$ ).
Mà \(\widehat {ACB} = \widehat {BDA};\;\;\;\widehat {BAD} \ne \widehat {BSA}\) (xét trong đường tròn đường kính $CM$ )
\( \Rightarrow \widehat {ASB} \ne \widehat {BCA} \Rightarrow \) tứ giác $ABCS$ không là tứ giác nội tiếp \( \Rightarrow \)phương án D sai.
Cho tam giác $ABC$ vuông tại $A$ và điểm $D$ nằm giữa $A$ và $B$ . Đường tròn đường kính $BD$ cắt $BC$ tại $E$. Các đường thẳng $CD$ , $AE$ lần lượt cắt đường tròn tại các điểm thứ hai là $F$ và $G$. Khi đó, kết luận không đúng là:
-
A.
$\Delta ABC\backsim\Delta EBD$.
-
B.
Tứ giác $ADEC$ là tứ giác nội tiếp.
-
C.
Tứ giác $AFBC$ không là tứ giác nội tiếp.
-
D.
Các đường thẳng $AC,DE$ và $BF$ đồng quy.
Đáp án : C
Góc nội tiếp chắn nửa đường tròn là góc vuông.
Tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn.
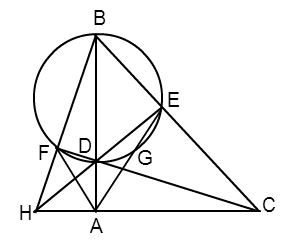
+) Xét đường tròn đường kính $BD$ có góc $BED$ là góc nội tiếp chắn nửa đường tròn nên \( \widehat {BED} = {90^0}.\)
Xét \(\Delta ABC\) và \(\Delta BED\) ta có: \(\widehat {DBE}\;\;chung\) và \(\widehat {BAC} = \widehat {BED} = {90^0}\) suy ra $\Delta ABC\backsim\Delta EBD\;\left( {g - g} \right)$
Vậy A đúng.
+) Do tam giác ADC vuông tại A (\(\widehat {DAC} = 90^0\)) và tam giác DEC vuông tại E (\(\widehat {DEC} = 90^0\)) nên tam giác ADC và tam giác DEC nội tiếp đường tròn đường kính DC.
Do đó tứ giác $ADEC$ là tứ giác nội tiếp. Vậy B đúng.
+) Chứng minh tương tự ta được tứ giác $AFBC$ là tứ giác nội tiếp. Vậy C sai.
+) Gọi giao điểm của $BF$ và $AC$ là $H$ .
Xét tam giác $BHC$ có hai đường cao $CF$ và $BA$ cắt nhau tại $D$. Do đó $D$ là trực tâm của tam giác $BHC$
Mà $DE = \bot AB$ nên $DE$ là đường cao của tam giác $BHC$ hay $H,E,D$ thẳng hàng.
Suy ra $DE,AC$ và $BF$ đồng quy tại $H$ suy ra D đúng.