Đề kiểm tra 45 phút chương 5: Hệ thức lượng trong tam giác vuông - Đề số 1
Đề bài
Cho $\alpha $ và $\beta $ là hai góc nhọn bất kỳ thỏa mãn $\alpha + \beta = 90^\circ $. Khẳng định nào sau đây là đúng ?
-
A.
$\tan \alpha = \sin \beta $
-
B.
$\tan \alpha = \cot \beta $
-
C.
$\tan \alpha = \cos \alpha $
-
D.
$\tan \alpha = \tan \beta $
Cho tam giác \(ABC\) vuông tại \(A,\) chiều cao \(AH\). Chọn câu sai.
-
A.
\(A{H^2} = BH.CH\)
-
B.
\(A{B^2} = BH.BC\)
-
C.
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)
-
D.
\(AH.AB = BC.AC\)
“Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng …” . Cụm từ thích hợp điền vào chỗ trống là
-
A.
Tích hai cạnh góc vuông
-
B.
Tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền
-
C.
Tích cạnh huyền và 1 cạnh góc vuông
-
D.
Tổng nghịch đảo các bình phương của hai cạnh góc vuông
Giải tam giác vuông $ABC,$ biết $\widehat A = 90^\circ \;$ và $BC = 50cm;\widehat B = {48^o}$ (làm tròn đến chữ số thập phân thứ nhất)
-
A.
\(AC = 37,2\,cm;\,AB = 33,4\,cm;\,\widehat C = 32^\circ \)
-
B.
\(AC = 37,2\,cm;\,AB = 33,5\,cm;\,\widehat C = 45^\circ \)
-
C.
\(AB = 37,2\,cm;\,AC = 33,5\,cm;\,\widehat C = 42^\circ \)
-
D.
\(AC = 37,2\,cm;\,AB = 33,5\,cm;\,\widehat C = 42^\circ \)
Cho tam giác $ABC$ vuông tại $A$ có $AB = 21\,cm$; $\widehat C = 40^\circ $ , phân giác \(BD\) (\(D\) thuộc \(AC\) ). Độ dài phân giác $BD$ là (Kết quả làm tròn đến chữ số thập phân thứ nhất)
-
A.
\(21,3\,cm\)
-
B.
\(24\,cm\)
-
C.
\(22,3\,cm\)
-
D.
\(23,2\,cm\)
Cho tam giác $ABC$ vuông tại $A$ có \(BC = 8\,cm,\,\,AC = 6cm.\) Tính tỉ số lượng giác $\tan C$ (làm tròn đến chữ số thập phân thứ $2$ ).
-
A.
$\tan C \approx 0,87$
-
B.
$\tan C \approx 0,86$
-
C.
$\tan C \approx 0,88$
-
D.
$\tan C \approx 0,89$
Một cầu trượt trong công viên có độ dốc là ${28^0}$ và có độ cao là $2,1m.$Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ hai).
-
A.
$3,95\,m$
-
B.
$3,8\,m$
-
C.
$4,5\,m$
-
D.
$4,47\,m$
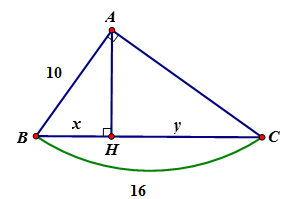
Tính \(x,y\) trong hình vẽ sau:
-
A.
\(x = 6,5;y = 9,5\)
-
B.
\(x = 6,25;y = 9,75\)
-
C.
\(x = 9,25;y = 6,75\)
-
D.
\(x = 6;y = 10\)
Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 1\,cm,\,\,BC = 2\,cm.\) Tính các tỉ số lượng giác \(\sin B;\cos B\)
-
A.
\(\sin B = \dfrac{1}{{\sqrt 3 }};\cos B = \dfrac{{2\sqrt 3 }}{3}\)
-
B.
\(\sin B = \dfrac{{\sqrt 5 }}{5};\cos B = \dfrac{{2\sqrt 5 }}{5}\)
-
C.
\(\sin B = \dfrac{1}{2};\cos B = \dfrac{2}{{\sqrt 5 }}\)
-
D.
\(\sin B = \dfrac{{2\sqrt 5 }}{5};\cos B = \dfrac{{\sqrt 5 }}{5}\)
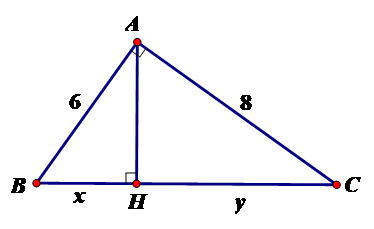
Tính $x,y$ trong hình vẽ sau:
-
A.
$x = 3,6;y = 6,4$
-
B.
$y = 3,6;x = 6,4$
-
C.
$x = 4;y = 6$
-
D.
$x = 2,8;y = 7,2$
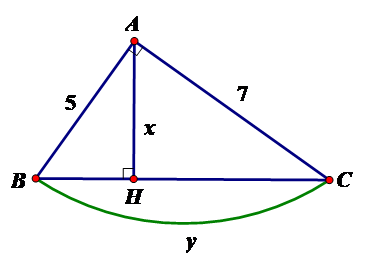
Tính $x,y$ trong hình vẽ sau:
-
A.
$x = \dfrac{{35\sqrt {74} }}{{74}};y = \sqrt {74} $
-
B.
$y = \dfrac{{35\sqrt {74} }}{{74}};x= \sqrt {74} $
-
C.
$x = 4;y = 6$
-
D.
$x = 2,8;y = 7,2$
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 9\,cm,\,\,\tan C = \dfrac{5}{4}\) . Tính độ dài các đoạn thẳng \(AC\) và \(BC\) . (làm tròn đến chữ số thập phân thứ \(2\) )
-
A.
\(AC = 11,53;BC = 7,2.\)
-
B.
\(AC = 7;BC \approx 11,53.\)
-
C.
\(AC = 5,2;BC \approx 11.\)
-
D.
\(AC = 7,2;BC \approx 11,53.\)
Cho tam giác $ABC$ có $\widehat B = {60^0},\widehat C = {50^0},AC = 3,5cm.$ Diện tích tam giác $ABC$ gần nhất với giá trị nào dưới đây?
-
A.
$4$
-
B.
$5$
-
C.
$7$
-
D.
$8$
Cho tam giác \(ABC\) có \(AB = 16,AC = 14\) và \(\widehat B = {60^0}\). Tính $BC$
-
A.
$BC = 10$
-
B.
$BC = 11$
-
C.
$BC = 9$
-
D.
$BC = 12$
Nhà bạn Vũ có một chiếc thang dài \(3,5\,m\). Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn” là \({62^0}\) (tức là đảm bảo thang không bị đổ khi sử dụng). (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(1,65\,m\)
-
B.
\(1,64\,\,m\)
-
C.
\(1,68\,m\)
-
D.
\(1,69\,m\)
Một cây tre cau \(8m\) bị gió bão làm gãy ngang thân, ngọn cây chạm đất cách gốc \(3,5m\) . Hỏi điểm gãy cách gốc bao nhiêu? (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(3,32\,m\)
-
B.
\(3,23\,m\)
-
C.
\(4\,m\)
-
D.
\(3\,m\)
Cho \(\Delta ABC\) vuông tại \(A.\) Biết $\dfrac{{AB}}{{AC}} = \dfrac{5}{7}$. Đường cao $AH = 15cm.$ Tính ${\rm{ }}HC.$
-
A.
\(\dfrac{{15\sqrt {74} }}{7}\)
-
B.
\(3\sqrt {74} \,cm\)
-
C.
\(22\,cm\)
-
D.
\(21\,cm\)
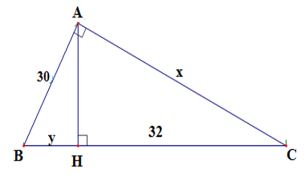
Tìm \(x;y\) trong hình vẽ sau:
-
A.
\(x = 30;y = 28\)
-
B.
\(x = 2\sqrt {481} ;y = \dfrac{{225}}{8}.\)
-
C.
\(x = 18;y = 40.\)
-
D.
\(x = 40;y = 18.\)
Cho đoạn thẳng $AB = 2a$ và trung điểm $O$ của nó. Trên nửa mặt phẳng bờ $AB$ vẽ các tia $Ax,By\;$ vuông góc với $AB.$ Qua \(O\) vẽ một tia cắt tia \(Ax\) tại $M$ sao cho $\widehat {AOM} = \alpha < {90^0}$ . Qua $O$ vẽ tia thứ hai cắt tia $By$ tại $N$ sao cho \(\widehat {MON} = 90^\circ \) . Khi đó, diện tích tam giác \(MON\) là
-
A.
\(\dfrac{{{a^2}}}{{2\sin \alpha .\cos \alpha }}\)
-
B.
\(\dfrac{{{a^2}}}{{\sin \alpha .\cos \alpha }}\)
-
C.
\(\dfrac{a}{{2\sin \alpha .\cos \alpha }}\)
-
D.
\(\dfrac{{2{a^2}}}{{\sin \alpha .\cos \alpha }}\)
Cho tam giác $ABC$ vuông tại $A$. Tính \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\).
-
A.
\(0\)
-
B.
\(1\)
-
C.
\( - 1\)
-
D.
\(2\)
Lời giải và đáp án
Cho $\alpha $ và $\beta $ là hai góc nhọn bất kỳ thỏa mãn $\alpha + \beta = 90^\circ $. Khẳng định nào sau đây là đúng ?
-
A.
$\tan \alpha = \sin \beta $
-
B.
$\tan \alpha = \cot \beta $
-
C.
$\tan \alpha = \cos \alpha $
-
D.
$\tan \alpha = \tan \beta $
Đáp án : B
Với hai góc \(\alpha ,\beta \) mà \(\alpha + \beta = {90^0}\).
Ta có: \(\sin \alpha = \cos \beta ;\cos \alpha = \sin \beta ;\)
\(\tan \alpha = \cot \beta ;\cot \alpha = \tan \beta \).
Cho tam giác \(ABC\) vuông tại \(A,\) chiều cao \(AH\). Chọn câu sai.
-
A.
\(A{H^2} = BH.CH\)
-
B.
\(A{B^2} = BH.BC\)
-
C.
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)
-
D.
\(AH.AB = BC.AC\)
Đáp án : D
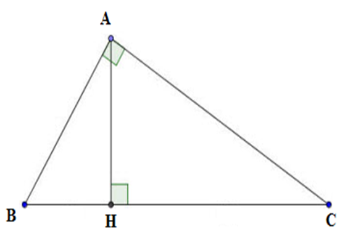
Ta thấy \(AH.BC = AB.AC\) nên D sai.
“Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng …” . Cụm từ thích hợp điền vào chỗ trống là
-
A.
Tích hai cạnh góc vuông
-
B.
Tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền
-
C.
Tích cạnh huyền và 1 cạnh góc vuông
-
D.
Tổng nghịch đảo các bình phương của hai cạnh góc vuông
Đáp án : B
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có hệ thức \(H{A^2} = HB.HC\)
Hay “Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng Tích hai hình chiếu của hai cạnh gọc vuông trên cạnh huyền”
Giải tam giác vuông $ABC,$ biết $\widehat A = 90^\circ \;$ và $BC = 50cm;\widehat B = {48^o}$ (làm tròn đến chữ số thập phân thứ nhất)
-
A.
\(AC = 37,2\,cm;\,AB = 33,4\,cm;\,\widehat C = 32^\circ \)
-
B.
\(AC = 37,2\,cm;\,AB = 33,5\,cm;\,\widehat C = 45^\circ \)
-
C.
\(AB = 37,2\,cm;\,AC = 33,5\,cm;\,\widehat C = 42^\circ \)
-
D.
\(AC = 37,2\,cm;\,AB = 33,5\,cm;\,\widehat C = 42^\circ \)
Đáp án : D
Giải tam giác vuông là tìm tất cả các cạnh và góc của tam giác vuông đó
Sử dụng các tỉ số lượng giác, định lý về góc trong tam giác, hệ thức liên hệ giữa cạnh và góc trong tam giác vuông.
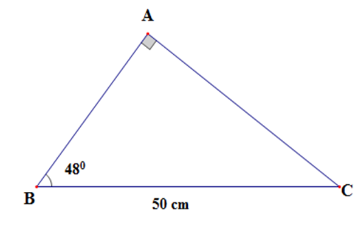
Xét $\Delta ABC$ có: $\widehat A = {90^o}$ $\widehat B + \widehat C = 90^\circ \Rightarrow \widehat C = 90^\circ - \widehat B = {90^o} - {48^o} = {42^o}$ ($\widehat C$ và $\widehat B$ là hai góc phụ nhau) Áp dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông ta có:
\(AC = BC.\sin B = 50.\sin 48^\circ \approx 37,2cm\)
\(AB = BC.\cos B = 50.\cos 48^\circ \approx 33,5cm\)
Vậy \(AC = 37,2\,cm;\,AB = 33,5\,cm;\,\widehat C = 42^\circ \) .
Cho tam giác $ABC$ vuông tại $A$ có $AB = 21\,cm$; $\widehat C = 40^\circ $ , phân giác \(BD\) (\(D\) thuộc \(AC\) ). Độ dài phân giác $BD$ là (Kết quả làm tròn đến chữ số thập phân thứ nhất)
-
A.
\(21,3\,cm\)
-
B.
\(24\,cm\)
-
C.
\(22,3\,cm\)
-
D.
\(23,2\,cm\)
Đáp án : D
+ Tính góc \(ABC\) từ đó suy ra góc \(ABD\)
+ Sử dụng hệ thức về cạnh và góc trong tam giác vuông \(ABD\) để tính \(BD.\)
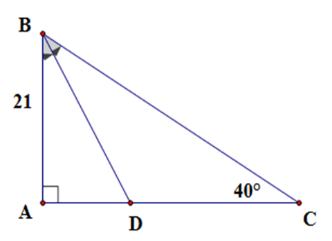
Xét tam giác \(ABC\) vuông tại \(A\) có \(\widehat {ABC} + \widehat C = 90^\circ \Rightarrow \widehat {ABC} = 50^\circ \)
Mà \(BD\) là phân giác góc \(ABC\) nên \(\widehat {ABD} = \dfrac{1}{2}\widehat {ABC} = 25^\circ \)
Xét tam giác \(ABD\) vuông tại \(A\) ta có \(BD = \dfrac{{AB}}{{\cos \widehat {ABD}}} = \dfrac{{21}}{{\cos 25^\circ }} \approx 23,2\,cm\)
Cho tam giác $ABC$ vuông tại $A$ có \(BC = 8\,cm,\,\,AC = 6cm.\) Tính tỉ số lượng giác $\tan C$ (làm tròn đến chữ số thập phân thứ $2$ ).
-
A.
$\tan C \approx 0,87$
-
B.
$\tan C \approx 0,86$
-
C.
$\tan C \approx 0,88$
-
D.
$\tan C \approx 0,89$
Đáp án : C
Bước 1: Tính cạnh còn lại theo định lý Pytago
Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn
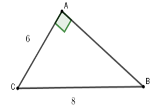
Theo định lý Py-ta-go ta có: $B{C^2} = A{C^2} + A{B^2} \Rightarrow AB = \sqrt {{8^2} - {6^2}} \approx 5,29$
Xét tam giác $ABC$ vuông tại $C$ có $\tan C = \dfrac{{AB}}{{AC}} \approx \dfrac{{5,29}}{6} \approx 0,88.$
Một cầu trượt trong công viên có độ dốc là ${28^0}$ và có độ cao là $2,1m.$Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ hai).
-
A.
$3,95\,m$
-
B.
$3,8\,m$
-
C.
$4,5\,m$
-
D.
$4,47\,m$
Đáp án : D
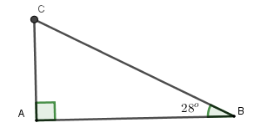
Ta có độ dài của mặt cầu trượt là $AB$; $AC = 2,1\,m$ và $\widehat {ABC} = 28^\circ $
Xét tam giác $ACB$ vuông tại $A$ có
$BC = AB:\sin B = 2,1:\sin 28^\circ \simeq 4,47\,m$
Vậy độ dài của mặt cầu trượt là $4,47\,m.$
Tính \(x,y\) trong hình vẽ sau:

-
A.
\(x = 6,5;y = 9,5\)
-
B.
\(x = 6,25;y = 9,75\)
-
C.
\(x = 9,25;y = 6,75\)
-
D.
\(x = 6;y = 10\)
Đáp án : B
Tính \(x\) theo hệ thức lượng \(A{B^2} = BH.BC\) từ đó suy ra \(y\).
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
\(A{B^2} = BH.BC \Leftrightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{100}}{{16}} = 6,25\) \( \Rightarrow CH = BC - BH = 16 - 6,25 = 9,75\)
Vậy \(x = 6,25;y = 9,75\)
Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 1\,cm,\,\,BC = 2\,cm.\) Tính các tỉ số lượng giác \(\sin B;\cos B\)
-
A.
\(\sin B = \dfrac{1}{{\sqrt 3 }};\cos B = \dfrac{{2\sqrt 3 }}{3}\)
-
B.
\(\sin B = \dfrac{{\sqrt 5 }}{5};\cos B = \dfrac{{2\sqrt 5 }}{5}\)
-
C.
\(\sin B = \dfrac{1}{2};\cos B = \dfrac{2}{{\sqrt 5 }}\)
-
D.
\(\sin B = \dfrac{{2\sqrt 5 }}{5};\cos B = \dfrac{{\sqrt 5 }}{5}\)
Đáp án : B
Bước 1: Tính cạnh còn lại theo định lý Pytago
Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn
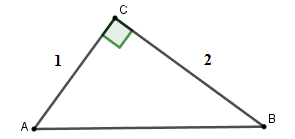
Theo định lý Py-ta-go ta có: \(A{B^2} = A{C^2} + B{C^2} \Rightarrow AB = \sqrt {{1^2} + {2^2}} = \sqrt 5 \)
Xét tam giác \(ABC\) vuông tại \(C\) có \(\sin B = \dfrac{{AC}}{{AB}} = \dfrac{1}{{\sqrt 5 }} = \dfrac{{\sqrt 5 }}{5}\) và \(\cos B = \dfrac{{BC}}{{AB}} = \dfrac{2}{{\sqrt 5 }} = \dfrac{{2\sqrt 5 }}{5}\)
Tính $x,y$ trong hình vẽ sau:

-
A.
$x = 3,6;y = 6,4$
-
B.
$y = 3,6;x = 6,4$
-
C.
$x = 4;y = 6$
-
D.
$x = 2,8;y = 7,2$
Đáp án : A
Bước 1: Tính $BC$ theo định lý Pytago
Bước 2: Tính $x,y$ theo hệ thức lượng $A{B^2} = BH.BC;A{C^2} = CH.BC$
Theo định lý Pytago ta có $B{C^2} = A{B^2} + A{C^2} \Leftrightarrow B{C^2} = 100 \Leftrightarrow BC = 10$
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} $
$= \dfrac{{{6^2}}}{10} = 3,6$ hay $x = 3,6$
$ \Rightarrow CH = BC - BH $$= 10 - 3,6 = 6,4.$
hay $y = 6,4$ .
Vậy $x = 3,6;y = 6,4.$
Tính $x,y$ trong hình vẽ sau:

-
A.
$x = \dfrac{{35\sqrt {74} }}{{74}};y = \sqrt {74} $
-
B.
$y = \dfrac{{35\sqrt {74} }}{{74}};x= \sqrt {74} $
-
C.
$x = 4;y = 6$
-
D.
$x = 2,8;y = 7,2$
Đáp án : A
Bước 1: Tính $BC$ theo định lý Pytago
Bước 2: Tính $x,y$ theo hệ thức lượng $AH.BC = AB.AC$
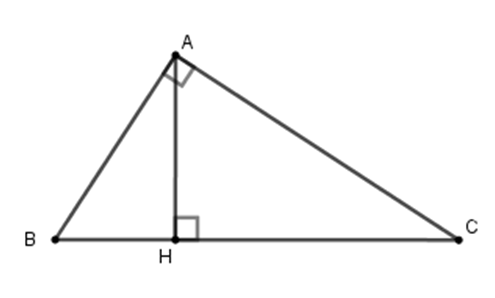
Theo định lý Pytago ta có $B{C^2} = A{B^2} + A{C^2} \Leftrightarrow B{C^2} = 74 \Leftrightarrow BC = \sqrt {74} $
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$AH.BC = AB.AC \Leftrightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{5.7}}{{\sqrt {74} }} = \dfrac{{35\sqrt {74} }}{{74}}$
Vậy $x = \dfrac{{35\sqrt {74} }}{{74}};y = \sqrt {74} $
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 9\,cm,\,\,\tan C = \dfrac{5}{4}\) . Tính độ dài các đoạn thẳng \(AC\) và \(BC\) . (làm tròn đến chữ số thập phân thứ \(2\) )
-
A.
\(AC = 11,53;BC = 7,2.\)
-
B.
\(AC = 7;BC \approx 11,53.\)
-
C.
\(AC = 5,2;BC \approx 11.\)
-
D.
\(AC = 7,2;BC \approx 11,53.\)
Đáp án : D
Sử dụng tỉ số lượng giác của góc nhọn, định lý Pytago để tính cạnh.
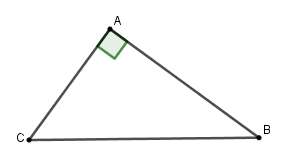
Vì tam giác \(ABC\) vuông tại \(A\) nên \(\tan C = \dfrac{{AB}}{{AC}} \Rightarrow AC = AB:\tan C = 9:\dfrac{5}{4} = 7,2cm\)
Theo định lý Pytago ta có \(B{C^2} = A{B^2} + A{C^2} = {9^2} + 7,{2^2} = 132,84 \Rightarrow BC = \dfrac{{9\sqrt {41} }}{5} \approx 11,53\)
Vậy \(AC = 7,2;BC \approx 11,53.\)
Cho tam giác $ABC$ có $\widehat B = {60^0},\widehat C = {50^0},AC = 3,5cm.$ Diện tích tam giác $ABC$ gần nhất với giá trị nào dưới đây?
-
A.
$4$
-
B.
$5$
-
C.
$7$
-
D.
$8$
Đáp án : B
+) Kẻ đường cao $AD$
+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông thích hợp và định lý Py-ta-go để tính cạnh.
+) Sử dụng công thức tính diện tích tam giác.
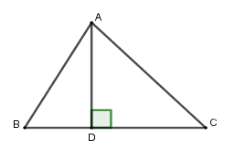
Kẻ đường cao \(AD\).
Xét tam giác vuông \(ACD\), có $AD = AC.\sin C = 3,5.\sin 50^\circ \approx 2,68\,cm$; $CD = AC.\cos C = 3,5.\cos 50^\circ \approx 2,25\,\,cm$
Xét tam giác vuông \(ABD\), có $BD = AD.\cot B \approx 2,68.\cot 60^\circ \approx 1,55\,\,cm$
Suy ra $BC = BD + CD = 3,8$
Do đó ${S_{ABC}} = \dfrac{{AD.BC}}{2} \approx 5,09$$c{m^2}$.
Cho tam giác \(ABC\) có \(AB = 16,AC = 14\) và \(\widehat B = {60^0}\). Tính $BC$
-
A.
$BC = 10$
-
B.
$BC = 11$
-
C.
$BC = 9$
-
D.
$BC = 12$
Đáp án : A
+) Kẻ đường cao $AH$
+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông thích hợp và định lý Py-ta-go để tính cạnh.
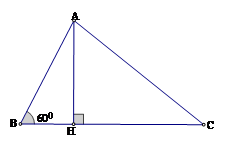
Kẻ đường cao \(AH\).
Xét tam giác vuông \(ABH\), ta có: \(BH = AB.\cos B = AB.\cos {60^0} = 16.\dfrac{1}{2} = 8\)\(AH = AB.\sin B = AB.\sin {60^0} = 16.\dfrac{{\sqrt 3 }}{2} = 8\sqrt 3 \).
Áp dụng định lý Pythago vào tam giác vuông \(AHC\) ta có:
\(H{C^2} = A{C^2} - A{H^2} = {14^2} - {\left( {8\sqrt 3 } \right)^2} = 196 - 192 = 4\). Suy ra \(HC = 2\). Vậy \(BC = CH + HB = 2 + 8 = 10\).
Nhà bạn Vũ có một chiếc thang dài \(3,5\,m\). Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn” là \({62^0}\) (tức là đảm bảo thang không bị đổ khi sử dụng). (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(1,65\,m\)
-
B.
\(1,64\,\,m\)
-
C.
\(1,68\,m\)
-
D.
\(1,69\,m\)
Đáp án : B
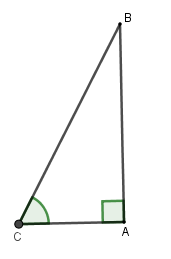
Ta có \(BC = 3,5\,\,m;\widehat C = 62^\circ \). Xét \(\Delta ABC\) vuông tại \(A\) có \(AC = BC.\cos \widehat C = 3,5.\cos 62^\circ \simeq 1,64\,\,m\).
Một cây tre cau \(8m\) bị gió bão làm gãy ngang thân, ngọn cây chạm đất cách gốc \(3,5m\) . Hỏi điểm gãy cách gốc bao nhiêu? (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(3,32\,m\)
-
B.
\(3,23\,m\)
-
C.
\(4\,m\)
-
D.
\(3\,m\)
Đáp án : B
Sử dụng định lý Py-ta-go trong tam giác vuông
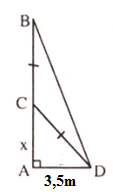
Giả sử \(AB\) là độ cao của cây tre, \(C\) là điểm gãy.
Đặt \(AC = x \Rightarrow CB = CD = 8-x\)
Vì \(\Delta ACD\) vuông tại \(A\)
\(⇒A{C^2} + A{D^2} = C{D^2}\)\( \Rightarrow {x^2} + 3,{5^2} = {\left( {8 - x} \right)^2}\)\( \Rightarrow 16x = \dfrac{{207}}{4} \)\(\Rightarrow x = \dfrac{{207}}{{64}} \approx 3,23m\)
Vậy điểm gãy cách gốc cây \(3,23\,m\)
Cho \(\Delta ABC\) vuông tại \(A.\) Biết $\dfrac{{AB}}{{AC}} = \dfrac{5}{7}$. Đường cao $AH = 15cm.$ Tính ${\rm{ }}HC.$
-
A.
\(\dfrac{{15\sqrt {74} }}{7}\)
-
B.
\(3\sqrt {74} \,cm\)
-
C.
\(22\,cm\)
-
D.
\(21\,cm\)
Đáp án : D
Đặt \(AB = 5a;AC = 7a\) \(\left( {a > 0} \right)\)
Sử dụng hệ thức lượng trong tam giác vuông một cách thích hợp để tìm \(HC.\)
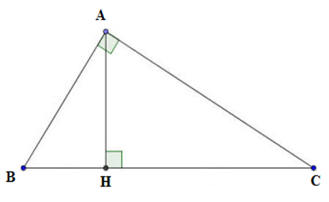
Vì \(\dfrac{{AB}}{{AC}} = \dfrac{5}{7} \Rightarrow AB = 5a;AC = 7a\) với \(a > 0.\)
Theo hệ thức lượng trong tam giác \(ABC\) vuông tại \(A\) ta có
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)
\( \Leftrightarrow \dfrac{1}{{{{15}^2}}} = \dfrac{1}{{{{\left( {5a} \right)}^2}}} + \dfrac{1}{{{{\left( {7a} \right)}^2}}}\) \( \Leftrightarrow \dfrac{1}{{225}} = \dfrac{1}{{25{a^2}}} + \dfrac{1}{{49{a^2}}} \Leftrightarrow \dfrac{1}{{225}} = \dfrac{{74}}{{1225{a^2}}} \Rightarrow {a^2} = \dfrac{{666}}{{49}} \Rightarrow a = \dfrac{{3\sqrt {74} }}{7}\)
Suy ra \(AB = \dfrac{{15\sqrt {74} }}{7};AC = 3\sqrt {74} \)
Lại có \(AH.BC = AB.AC \Rightarrow BC = \dfrac{{AB.AC}}{{AH}} = \dfrac{{222}}{7}\)
Mà \(A{C^2} = CH.BC \Rightarrow HC = \dfrac{{A{C^2}}}{{BC}} = 21\,cm.\)
Tìm \(x;y\) trong hình vẽ sau:

-
A.
\(x = 30;y = 28\)
-
B.
\(x = 2\sqrt {481} ;y = \dfrac{{225}}{8}.\)
-
C.
\(x = 18;y = 40.\)
-
D.
\(x = 40;y = 18.\)
Đáp án : D
Áp dụng hệ thức lượng trong tam giác vuông \(A{B^2} = BH.BC;A{C^2} = CH.BC\)
Ta có \(BC = BH + HC = y + 32\)
Áp dụng hệ thức lượng \(A{B^2} = BH.BC\) trong tam giác vuông \(ABC\) ta có
\(\begin{array}{l}{30^2} = y\left( {y + 32} \right)\\ \Leftrightarrow {y^2} + 32y - 900 = 0\\ \Leftrightarrow {y^2} + 50y - 18y - 90 = 0\\ \Leftrightarrow y\left( {y + 50} \right) - 18\left( {y + 50} \right) = 0\\ \Leftrightarrow \left( {y - 18} \right)\left( {y + 50} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}y - 18 = 0\\y + 50 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}y = 18\left( N \right)\\y = - 50\,\left( L \right)\end{array} \right.\end{array}\)
Suy ra \(y = 18 \Rightarrow BC = 18 + 32 = 50\)
Áp dụng hệ thức lượng \(A{C^2} = CH.BC\) ta có
\({x^2} = 32.50 \Leftrightarrow {x^2} = 1600 \Rightarrow x = 40.\)
Vậy \(x = 40;y = 18.\)
Cho đoạn thẳng $AB = 2a$ và trung điểm $O$ của nó. Trên nửa mặt phẳng bờ $AB$ vẽ các tia $Ax,By\;$ vuông góc với $AB.$ Qua \(O\) vẽ một tia cắt tia \(Ax\) tại $M$ sao cho $\widehat {AOM} = \alpha < {90^0}$ . Qua $O$ vẽ tia thứ hai cắt tia $By$ tại $N$ sao cho \(\widehat {MON} = 90^\circ \) . Khi đó, diện tích tam giác \(MON\) là
-
A.
\(\dfrac{{{a^2}}}{{2\sin \alpha .\cos \alpha }}\)
-
B.
\(\dfrac{{{a^2}}}{{\sin \alpha .\cos \alpha }}\)
-
C.
\(\dfrac{a}{{2\sin \alpha .\cos \alpha }}\)
-
D.
\(\dfrac{{2{a^2}}}{{\sin \alpha .\cos \alpha }}\)
Đáp án : A
Áp dụng hệ thức về cạnh và góc trong tam giác vuông
Áp dụng công thức tính diện tích tam giác vuông
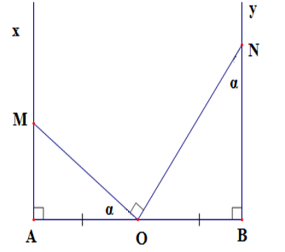
Theo đề bài ta có: \(AB = 2a \Rightarrow OA = OB = a\)
Ta có: \(\widehat {ONB} = \widehat {AOM} = \alpha \) (cùng phụ với \(\widehat {BON}\) )
Xét \(\Delta AOM\) có \(\widehat A = 90^\circ \) Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
\(OA = OM.\cos \alpha \Rightarrow OM = \dfrac{a}{{\cos \alpha }}\) Xét \(\Delta BON\) có \(\widehat B = 90^\circ \) Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
\(OB = ON.\sin \alpha \Rightarrow ON = \dfrac{a}{{\sin \alpha }}\) Vậy diện tích tam giác \(MON\) là: \(\dfrac{1}{2}OM.ON = \dfrac{1}{2}.\dfrac{a}{{\cos \alpha }}.\dfrac{a}{{\sin \alpha }} = \dfrac{{{a^2}}}{{2\sin \alpha .\cos \alpha }}\)
Cho tam giác $ABC$ vuông tại $A$. Tính \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\).
-
A.
\(0\)
-
B.
\(1\)
-
C.
\( - 1\)
-
D.
\(2\)
Đáp án : A
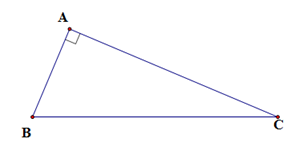
Ta có: \(\sin B = \dfrac{{AC}}{{BC}} \Rightarrow {\sin ^2}B = \dfrac{{A{C^2}}}{{B{C^2}}}\)
\(\sin C = \dfrac{{AB}}{{BC}} \Rightarrow {\sin ^2}C = \dfrac{{A{B^2}}}{{B{C^2}}}\;\;\)
\(\tan B = \dfrac{{AC}}{{AB}} \); \( \tan C = \dfrac{{AB}}{{AC}}\)
Vậy \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C\;\)
\( = \dfrac{{A{C^2}}}{{B{C^2}}} + \dfrac{{A{B^2}}}{{B{C^2}}} - \dfrac{{AC}}{{AB}}.\dfrac{{AB}}{{AC}} = \dfrac{{A{C^2} + A{B^2}}}{{B{C^2}}} - 1\)
\( = \dfrac{{B{C^2}}}{{B{C^2}}} - 1 = 0\) (vì theo định lý Pytago thì \(A{C^2} + A{B^2} = B{C^2}\) )