Đề kiểm tra 45 phút chương 7: Góc với đường tròn - Đề số 1
Đề bài
Cho hình vẽ dưới đây, góc \(DIE\) có số đo bằng
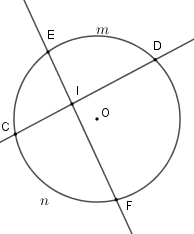
-
A.
$\dfrac{1}{2}$(sđ \(\overparen{DmE} + \) sđ \(\overparen{CnF}\) )
-
B.
$\dfrac{1}{2}$(sđ \(\overparen{DmE} - \) sđ \(\overparen{CnF}\) )
-
C.
$\dfrac{1}{2}$(sđ \(\overparen{DF} + \) sđ \(\overparen{CE}\) )
-
D.
$\dfrac{1}{2}$(sđ \(\overparen{DF} + \) sđ \(\overparen{CE}\) )
Góc nội tiếp nhỏ hơn hoặc bằng \(90^\circ \) có số đo
-
A.
Bằng nửa số đo góc ở tâm cùng chắn một cung
-
B.
Bằng số đo của góc ở tâm cùng chắn một cung
-
C.
Bằng số đo cung bị chắn
-
D.
Bằng nửa số đo cung lớn.
Chọn khẳng định đúng. Cho đường tròn $\left( O \right)$ có dây $AB > CD$ khi đó
-
A.
Cung $AB$ lớn hơn cung $CD$
-
B.
Cung $AB$ nhỏ hơn cung $CD$
-
C.
Cung $AB$ bằng cung $CD$
-
D.
Số đo cung $AB$ bằng hai lần số đo cung $CD$
Kết luận nào sau đây là đúng.
-
A.
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo lớn hơn số đo góc nội tiếp chắn cung đó.
-
B.
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo nhỏ hơn số đo góc nội tiếp chắn cung đó.
-
C.
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
-
D.
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo bằng hai lần số đo của góc nội tiếp chắn cung đó.
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) và \(C\) là điểm trên cung nhỏ \(AB\) (cung \(CB\) nhỏ hơn cung \(CA\) ). Tiếp tuyến tại \(C\) của nửa đường tròn cắt đường thẳng \(AB\) tại \(D\) . Biết tam giác \(ADC\) cân tại \(C\) . Tính góc \(ADC\) .
-
A.
$40^\circ $
-
B.
$45^\circ $
-
C.
$60^\circ $
-
D.
$30^\circ $
Cho đường tròn $(O)$ đường kính $AB$ và một cung $AC$ có số đo nhỏ hơn $90^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai ?
-
A.
$AC = BE$
-
B.
Số đo cung$AD$ bằng số đo cung $BE$
-
C.
Số đo cung $AC$ bằng số đo cung $BE$
-
D.
$\widehat {AOC} < \widehat {AOD}$
Cho hình vẽ dưới đây.
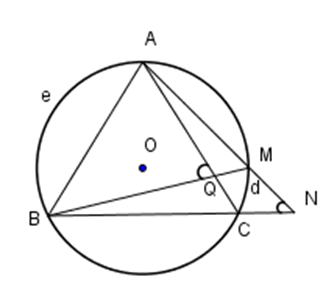
Khi đó mệnh đề đúng là:
-
A.
\(\widehat {AQB} = \widehat {ANB}\)
-
B.
\(\widehat {AQB} > \widehat {ANB}\)
-
C.
\(\widehat {AQB} < \widehat {ANB}\)
-
D.
Tất cả đều sai
Cho tam giác \(ABC\) cân tại \(A\) nội tiếp đường tròn tâm \(O.\) Trên \(\left( O \right)\) lấy điểm \(D\) thuộc cung \(AC\). Gọi \(E = AC \cap BD,\,\,F = AD \cap BC.\) Khi đó mệnh đề đúng là:
-
A.
\(\widehat {AFB} > \widehat {ABD}\)
-
B.
\(\widehat {AFB} < \widehat {ABD}\)
-
C.
\(\widehat {AFB} = 2\widehat {ABD}\)
-
D.
\(\widehat {AFB} = \widehat {ABD}\)
Cho ba điểm $A,B,C$ thẳng hàng sao cho $B$ nằm giữa $A$ và $C$ . Chọn khẳng định nào sau đây đúng ?
-
A.
Độ dài nửa đường tròn đường kính $AC$ bằng hiệu các độ dài của hai nửa đường tròn đường kính $AB$ và $BC$
-
B.
Độ dài nửa đường tròn đường kính $AC$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AB$ và $BC$ .
-
C.
Độ dài nửa đường tròn đường kính $BC$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AB$ và $AC$
-
D.
Độ dài nửa đường tròn đường kính $AB$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AC$ và $BC$
Một hình tròn có diện tích \(S = 144\pi \,\left( {c{m^2}} \right)\) . Bán kính của hình tròn đó là:
-
A.
$15\,\left( {cm} \right)$
-
B.
$16\,\left( {cm} \right)$
-
C.
$12\,\left( {cm} \right)$
-
D.
$14\,\left( {cm} \right)$
Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính \(BC.\) Lấy điểm \(A\) trên tia đối của tia \(CB.\) Kẻ tiếp tuyến $AF,Bx$ của nửa đường tròn \(\left( O \right)\) (với \(F\) là tiếp điểm). Tia \(AF\) cắt tia \(Bx\) của nửa đường tròn tại \(D.\) Khi đó tứ giác \(OBDF\) là:
-
A.
Hình thang
-
B.
Tứ giác nội tiếp
-
C.
Hình thang cân
-
D.
Hình bình hành
Tứ giác $ABCD$ nội tiếp đường tròn có hai cạnh đối $AB$ và $CD$ cắt nhau tại $M$ và $\widehat {BAD} = {70^0}$ thì $\widehat {BCM} = ?$
-
A.
\({110^0}\)
-
B.
\({30^0}\)
-
C.
\({70^0}\)
-
D.
\({55^0}\)
Cho tam giác ABC nằm trên đường tròn $(O;R), $đường cao $AH,$ biết $AB = 9{\rm{ }}cm,$ $AC = 12{\rm{ }}cm,$ $AH = 4{\rm{ }}cm.$ Tính bán kính của đường tròn $(O)$.
-
A.
\(13,5\,cm\)
-
B.
$12\,cm$
-
C.
\(18\,cm\)
-
D.
$6\,cm$
Cho nửa đường tròn $(O)$ đường kính $AB$ và một điểm $C$ trên nửa đường tròn. Gọi $D$ là một điểm trên đường kính $AB$; qua $D$ kẻ đường vuông góc với $AB$ cắt $BC$ tại $F$, cắt $AC$ tại $E$. Tiếp tuyến của nửa đường tròn tại $C$cắt $EF$ tại $I.$Khi đó
-
A.
\(IE = IF\)
-
B.
\(IE = 2IF\)
-
C.
$EF = 3IE$
-
D.
\(EF = 3IF\)
Cho \(\left( {O;4} \right)\) có dây \(AC\) bằng cạnh hình vuông nội tiếp và dây \(BC\) bằng cạnh tam giác đều nội tiếp đường tròn đó ( điểm \(C\) và \(A\) nằm cùng phía với \(BO\) ). Tính số đo góc \(ACB\)
-
A.
\(30^\circ \)
-
B.
\(45^\circ \)
-
C.
\(60^\circ \)
-
D.
\(15^\circ \)
Cho \(\Delta ABC\) vuông ở $A$ . Trên cạnh $AC$ lấy điểm $M$ và vẽ đường tròn đường kính $MC$ . Kẻ $BM$ cắt đường tròn tại $D$ . Đường thẳng $DA$ cắt đường tròn tại $S$ . Chọn đáp án sai trong các đáp án sau:
-
A.
Tứ giác $ABCD$ nội tiếp.
-
B.
\(\widehat {ABD} = \widehat {ACD}\)
-
C.
$CA$ là phân giác của \(\widehat {SCB}.\)
-
D.
Tứ giác $ABCS$ nội tiếp.
Ch u vi đường tròn ngoại tiếp tam giác đều cạnh \(a\,\left( {cm} \right)\) là
-
A.
$\dfrac{{4\pi a\sqrt 3 }}{3} (cm)$
-
B.
$\dfrac{{2\pi a\sqrt 3 }}{3} (cm)$
-
C.
$\dfrac{{\pi a\sqrt 3 }}{3} (cm)$
-
D.
$\dfrac{{5\pi a\sqrt 3 }}{3}(cm)$
Cho tam giác đều \(ABC\) nội tiếp đường tròn \(\left( O \right)\). Độ dài của các cung \(AB,BC,CA\) đều bằng \(4\pi \). Diện tích của tam giác đều \(ABC\) là:
-
A.
\(27\sqrt 3 \) $cm^2$
-
B.
\(7\sqrt 3 \) $cm^2$
-
C.
\(29\sqrt 3 \) $cm^2$
-
D.
\(9\sqrt 3 \) $cm^2$
Từ điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(MA, MB\) với \(\left( O \right)\) tại \(A\) và \(B.\) Qua \(A\) vẽ đường thẳng song song với \(MB\) cắt đường tròn tại \(C.\)
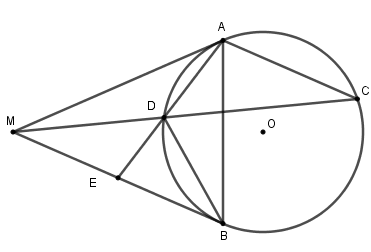
Nối \(C\) với \(M\) cắt đường tròn \(\left( O \right)\) tại \(D.\) Nối \(A\) với \(D\) cắt \(MB\) tại \(E.\) Chọn câu đúng
-
A.
\(ME = 2EB\)
-
B.
\(2ME = EB\)
-
C.
\(ME = EB.\)
-
D.
\(3ME = 2EB\)
Cho \(A\) là điểm cố định trên đường tròn \(\left( {O;R} \right).\) Gọi \(AB\) và \(AC\) là hai dây cung thay đổi trên đường tròn \(\left( O \right)\) thỏa mãn \(\sqrt {AB.AC} = R\sqrt 3 .\) Khi đó vị trí của \(B,\,C\) trên \(\left( O \right)\) để diện tích \(\Delta ABC\) lớn nhất là:
-
A.
\(\Delta ABC\) cân
-
B.
\(\Delta ABC\) đều.
-
C.
\(\Delta ABC\) vuông cân
-
D.
\(\Delta ABC\) vuông
Lời giải và đáp án
Cho hình vẽ dưới đây, góc \(DIE\) có số đo bằng

-
A.
$\dfrac{1}{2}$(sđ \(\overparen{DmE} + \) sđ \(\overparen{CnF}\) )
-
B.
$\dfrac{1}{2}$(sđ \(\overparen{DmE} - \) sđ \(\overparen{CnF}\) )
-
C.
$\dfrac{1}{2}$(sđ \(\overparen{DF} + \) sđ \(\overparen{CE}\) )
-
D.
$\dfrac{1}{2}$(sđ \(\overparen{DF} + \) sđ \(\overparen{CE}\) )
Đáp án : A
Số đo của góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
\(\widehat {DIE} = \)$\dfrac{1}{2}$(sđ \(\overparen{DmE} + \) sđ \(\overparen{CnF}\) )
Góc nội tiếp nhỏ hơn hoặc bằng \(90^\circ \) có số đo
-
A.
Bằng nửa số đo góc ở tâm cùng chắn một cung
-
B.
Bằng số đo của góc ở tâm cùng chắn một cung
-
C.
Bằng số đo cung bị chắn
-
D.
Bằng nửa số đo cung lớn.
Đáp án : A
Dựa vào Định lí mối liên hệ giữa góc nội tiếp với cung bị chắn :
Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Trong một đường tròn:
Góc nội tiếp (nhỏ hơn hoặc bằng $90^\circ $) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.
Chọn khẳng định đúng. Cho đường tròn $\left( O \right)$ có dây $AB > CD$ khi đó
-
A.
Cung $AB$ lớn hơn cung $CD$
-
B.
Cung $AB$ nhỏ hơn cung $CD$
-
C.
Cung $AB$ bằng cung $CD$
-
D.
Số đo cung $AB$ bằng hai lần số đo cung $CD$
Đáp án : A
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
+) Cung lớn hơn căng dây lớn hơn.
+) Dây lớn hơn căng cung lớn hơn.
Nên dây $AB > CD$ thì cung $AB$ lớn hơn cung $CD$
Kết luận nào sau đây là đúng.
-
A.
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo lớn hơn số đo góc nội tiếp chắn cung đó.
-
B.
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo nhỏ hơn số đo góc nội tiếp chắn cung đó.
-
C.
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
-
D.
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo bằng hai lần số đo của góc nội tiếp chắn cung đó.
Đáp án : C
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) và \(C\) là điểm trên cung nhỏ \(AB\) (cung \(CB\) nhỏ hơn cung \(CA\) ). Tiếp tuyến tại \(C\) của nửa đường tròn cắt đường thẳng \(AB\) tại \(D\) . Biết tam giác \(ADC\) cân tại \(C\) . Tính góc \(ADC\) .
-
A.
$40^\circ $
-
B.
$45^\circ $
-
C.
$60^\circ $
-
D.
$30^\circ $
Đáp án : D
Sử dụng góc nội tiếp và góc có đỉnh bên ngoài đường tròn
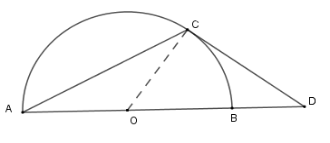
Xét nửa \(\left( O \right)\) có \(\widehat {BAC} = \dfrac{1}{2}\) sđ \(\overparen{BC}\) (góc nội tiếp chắn cung BC) và \(\widehat {CDA} = \dfrac{1}{2}\) (sđ \(\overparen{AC} - \) sđ \(\overparen{BC}\) ) (góc có đỉnh bên ngoài đường tròn)
Mà \(\Delta ADC\) cân tại \(C\) nên \(\widehat {DAC} = \widehat {CDA} \Leftrightarrow \) sđ \(\overparen{BC} = \) sđ \(\overparen{AC} - \) sđ \(\overparen{BC}\)
Suy ra sđ \(\overparen{AC} = 2\). sđ \(\overparen{BC}\)
Mà sđ \(\overparen{AC} + \) sđ \(\overparen{BC} = 180^\circ \) nên sđ \(\overparen{AC} = 120^\circ \) ; sđ\(\overparen{BC}= 60^\circ \)
Do đó $\widehat {ADC} = 30^\circ $.
Cho đường tròn $(O)$ đường kính $AB$ và một cung $AC$ có số đo nhỏ hơn $90^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai ?
-
A.
$AC = BE$
-
B.
Số đo cung$AD$ bằng số đo cung $BE$
-
C.
Số đo cung $AC$ bằng số đo cung $BE$
-
D.
$\widehat {AOC} < \widehat {AOD}$
Đáp án : D
Sử dụng liên hệ giữa dây và đường kính để so sánh các góc ở tâm từ đó so sánh các cung và dây cung
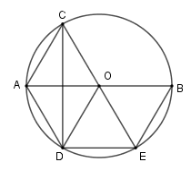
Vì $AO \bot CD;AO{\rm{//}}DE \Rightarrow CD \bot DE$$ \Rightarrow \widehat {CDE} = 90^\circ $ mà $C,D,E \in \left( O \right)$ nên $CE$ là đường kính hay $C;O;E$ thẳng hàng
Xét $\left( O \right)$ có $OA$ là đường cao trong tam giác cân $ODC$ nên $OA$ cũng là đường phân giác $ \Rightarrow \widehat {COA} = \widehat {AOD}$
Suy ra cung $AD$ bằng cung $AC$ nên dây $AD = AC$
Lại thấy $\widehat {AOC} = \widehat {BOE}$ (đối đỉnh) nên cung $AC$ bằng cung $BE$ suy ra dây $AC = BE$.
Phương án A, B, C đúng.
Cho hình vẽ dưới đây.

Khi đó mệnh đề đúng là:
-
A.
\(\widehat {AQB} = \widehat {ANB}\)
-
B.
\(\widehat {AQB} > \widehat {ANB}\)
-
C.
\(\widehat {AQB} < \widehat {ANB}\)
-
D.
Tất cả đều sai
Đáp án : B
- Tính chất góc có đỉnh nằm trong đường tròn: Số đo góc có đỉnh nằm trong đường tròn có số đo bằng nửa tổng số đo hai cung bị chắn.
- Tính chất góc có đỉnh nằm ngoài đường tròn: Số đo góc có đỉnh nằm ngoài đường tròn có số đo bằng nửa hiệu số đo hai cung bị chắn.
Ta áp dụng công thức về góc có đỉnh ở trong và ở ngoài đường tròn bị chắn bởi cung ta nhận được
\(\left\{ \begin{array}{l}\widehat {AQB} = \dfrac{1}{2}\left( {sđ\overparen{AeB} + sđ\overparen{CdM}} \right)\,\,\\\widehat {ANB} = \dfrac{1}{2}\left( {sđ\overparen{AeB} - sđ\overparen{CdM}} \right)\,\,\end{array} \right. \)\(\Rightarrow \widehat {AQB} = \dfrac{1}{2}\left( {sđ\overparen{AeB} + sđ\overparen{CdM}} \right) > \dfrac{1}{2}\left( {sđ\overparen{AeB} - sđ\overparen{CdM}} \right) = \widehat {ANB}.\)
Cho tam giác \(ABC\) cân tại \(A\) nội tiếp đường tròn tâm \(O.\) Trên \(\left( O \right)\) lấy điểm \(D\) thuộc cung \(AC\). Gọi \(E = AC \cap BD,\,\,F = AD \cap BC.\) Khi đó mệnh đề đúng là:
-
A.
\(\widehat {AFB} > \widehat {ABD}\)
-
B.
\(\widehat {AFB} < \widehat {ABD}\)
-
C.
\(\widehat {AFB} = 2\widehat {ABD}\)
-
D.
\(\widehat {AFB} = \widehat {ABD}\)
Đáp án : D
Áp dụng tính chất góc nội tiếp, góc có đỉnh nằm ngoài đường tròn, các cung chắn hai dây bằng nhau để chứng minh \(\widehat {AFB} = \widehat {ABD}.\)
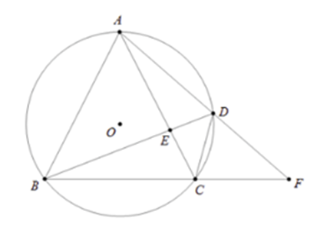
\(\Delta ABC\) cân tại \(A\) nên \(AB = AC\) suy ra \(sđ\,\overparen{AB} = sđ\,\overparen{AC}.\)
Áp dụng kết quả trên và theo tính chất của góc ngoài đường tròn ta có:
$\widehat {AFB} = \dfrac{1}{2}\left( {sđ\,\overparen{AB} - sđ\,\overparen{CD}} \right) = \dfrac{1}{2}\left( {sđ\,\overparen{AC} - sđ\,\overparen{CD}} \right) = \dfrac{1}{2}sđ\,\overparen{AD}.$
Mặt khác theo tính chất góc nội tiếp ta có \(\widehat {ABD} = \dfrac{1}{2}sđ\,\overparen{AD}.\)
Do đó \(\widehat {AFB} = \widehat {ABD}.\)
Cho ba điểm $A,B,C$ thẳng hàng sao cho $B$ nằm giữa $A$ và $C$ . Chọn khẳng định nào sau đây đúng ?
-
A.
Độ dài nửa đường tròn đường kính $AC$ bằng hiệu các độ dài của hai nửa đường tròn đường kính $AB$ và $BC$
-
B.
Độ dài nửa đường tròn đường kính $AC$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AB$ và $BC$ .
-
C.
Độ dài nửa đường tròn đường kính $BC$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AB$ và $AC$
-
D.
Độ dài nửa đường tròn đường kính $AB$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AC$ và $BC$
Đáp án : B
Sử dụng công thức tính độ dài nửa đường tròn bán kính $R$ (nửa chu vi đường tròn):
\(l = \pi R\).
Độ dài nửa đường tròn đường kính \(AC\) là \({l_1} = \pi .\dfrac{{AC}}{2}\) .
Độ dài nửa đường tròn đường kính \(AB\) là \({l_1} = \pi .\dfrac{{AB}}{2}\) .
Độ dài nửa đường tròn đường kính \(BC\) là \({l_1} = \pi .\dfrac{{BC}}{2}\) .
Mà ba điểm $A,B,C$ thẳng hàng sao cho $B$ nằm giữa $A$ và $C$ nên \(AB + BC = AC\)
Do đó \({l_1} = \pi .\dfrac{{AC}}{2} = \pi \left( {\dfrac{{AB}}{2} + \dfrac{{BC}}{2}} \right) = \pi .\dfrac{{AB}}{2} + \pi .\dfrac{{BC}}{2} = {l_2} + {l_3}\)
Vậy độ dài nửa đường tròn đường kính $AC$ bằng tổng các độ dài của hai nửa đường tròn đường kính $AB$ và $BC$ .
Một hình tròn có diện tích \(S = 144\pi \,\left( {c{m^2}} \right)\) . Bán kính của hình tròn đó là:
-
A.
$15\,\left( {cm} \right)$
-
B.
$16\,\left( {cm} \right)$
-
C.
$12\,\left( {cm} \right)$
-
D.
$14\,\left( {cm} \right)$
Đáp án : C
Sử dụng công thức: Diện tích $S$ của một hình tròn bán kính $R$ là \(S = \pi {R^2}.\)
Diện tích \(S = \pi {R^2} = 144\pi \Leftrightarrow {R^2} = 144 \Leftrightarrow R = 12\,\left( {cm} \right)\).
Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính \(BC.\) Lấy điểm \(A\) trên tia đối của tia \(CB.\) Kẻ tiếp tuyến $AF,Bx$ của nửa đường tròn \(\left( O \right)\) (với \(F\) là tiếp điểm). Tia \(AF\) cắt tia \(Bx\) của nửa đường tròn tại \(D.\) Khi đó tứ giác \(OBDF\) là:
-
A.
Hình thang
-
B.
Tứ giác nội tiếp
-
C.
Hình thang cân
-
D.
Hình bình hành
Đáp án : B
Tứ giác có tổng một cặp góc đối bằng \({180^0}\) là tứ giác nội tiếp.
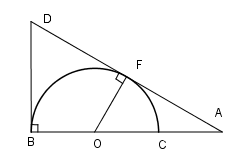
Ta có \(\widehat {DBO} = {90^0}\) và \(\widehat {DFO} = {90^0}\) ( tính chất tiếp tuyến).
Tứ giác \(OBDF\) có \(\widehat {DBO} + \widehat {DFO} = {90^0} + {90^0} = {180^0}\) nên nội tiếp được trong một đường tròn.
Tứ giác $ABCD$ nội tiếp đường tròn có hai cạnh đối $AB$ và $CD$ cắt nhau tại $M$ và $\widehat {BAD} = {70^0}$ thì $\widehat {BCM} = ?$
-
A.
\({110^0}\)
-
B.
\({30^0}\)
-
C.
\({70^0}\)
-
D.
\({55^0}\)
Đáp án : C
Áp dụng tính chất tứ giác nội tiếp có tổng hai góc đối diện bằng \({180^0}.\)
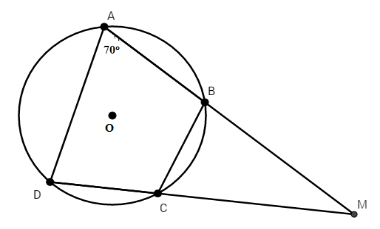
Tứ giác $ABCD$ nội tiếp nên có: $\widehat {DAB} + \widehat {BCD} = {180^\circ}$ suy ra $\widehat {BCD} = {180^\circ} - {70^\circ} = {110^\circ}$
Mà $\widehat {BCD} + \widehat {BCM} = {180^\circ}$ (kề bù)
Do đó $\widehat {BCM} = {180^\circ} - {110^\circ} = {70^\circ}$
Cho tam giác ABC nằm trên đường tròn $(O;R), $đường cao $AH,$ biết $AB = 9{\rm{ }}cm,$ $AC = 12{\rm{ }}cm,$ $AH = 4{\rm{ }}cm.$ Tính bán kính của đường tròn $(O)$.
-
A.
\(13,5\,cm\)
-
B.
$12\,cm$
-
C.
\(18\,cm\)
-
D.
$6\,cm$
Đáp án : A
Kẻ đường kính \(AD\)
Chứng minh \(\Delta ACH \backsim \Delta ADB\left( {g - g} \right)\)
Suy ra \( AD = \dfrac{{AB.AC}}{{AH}}\)
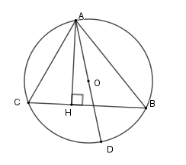
Kẻ đường kính \(AD\)
Xét \(\left( O \right)\) có \(\widehat {ACB} = \widehat {ADB}\) (hai góc nội tiếp cùng chắn cung \(AB\) ); \(\widehat {ABD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Nên \(\Delta ACH \backsim \Delta ADB\left( {g - g} \right)\)
Suy ra $\dfrac{{AC}}{{AD}} = \dfrac{{AH}}{{AB}}$
Do đó $AH.AD = AC.AB$
Suy ra \(AD = \dfrac{{AB.AC}}{{AH}} = \dfrac{{9.12}}{4} = 27\)
Do đó \(R = 13,5cm\) .
Cho nửa đường tròn $(O)$ đường kính $AB$ và một điểm $C$ trên nửa đường tròn. Gọi $D$ là một điểm trên đường kính $AB$; qua $D$ kẻ đường vuông góc với $AB$ cắt $BC$ tại $F$, cắt $AC$ tại $E$. Tiếp tuyến của nửa đường tròn tại $C$cắt $EF$ tại $I.$Khi đó
-
A.
\(IE = IF\)
-
B.
\(IE = 2IF\)
-
C.
$EF = 3IE$
-
D.
\(EF = 3IF\)
Đáp án : A
Sử dụng hệ quả góc tạo bởi tia tiếp tuyến và dây cung để chứng minh hai góc bằng nhau.
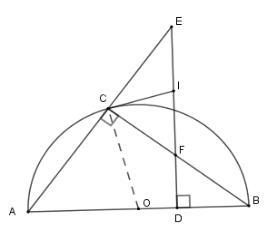
Xét \(\left( O \right)\) có $\widehat {ICB} = \widehat {CAB}$ (hệ quả) mà $\widehat {BFD} = \widehat {BAC}$ (cùng phụ với \(\widehat {ABC}\) )
Nên \(\widehat {ICF} = \widehat {BFD} \Rightarrow \widehat {ICF} = \widehat {CFI}\) suy ra \(\Delta ICF\) cân tại \(I \Rightarrow IF = IC\) (*)
Lại có \(\widehat {ICE} + \widehat {ICF} = 90^\circ \Rightarrow \widehat {ICE} + \widehat {CAB} = 90^\circ \) mà \(\widehat {CAB} + \widehat {AED} = 90^\circ \Rightarrow \widehat {CEI} = \widehat {ECI} \Rightarrow \Delta ICE\) cân tại \(I\)
Nên \(IE = IC\) (**)
Từ (*) và (**) suy ra \(IE = IF = \dfrac{{EF}}{2}\) .
Cho \(\left( {O;4} \right)\) có dây \(AC\) bằng cạnh hình vuông nội tiếp và dây \(BC\) bằng cạnh tam giác đều nội tiếp đường tròn đó ( điểm \(C\) và \(A\) nằm cùng phía với \(BO\) ). Tính số đo góc \(ACB\)
-
A.
\(30^\circ \)
-
B.
\(45^\circ \)
-
C.
\(60^\circ \)
-
D.
\(15^\circ \)
Đáp án : D
+ Tìm số đo các cung \(BC\) và \(AB\) để tìm số đo cung \(AC\)
+ Sử dụng: số đo góc nội tiếp bằng nửa số đo cung bị chắn
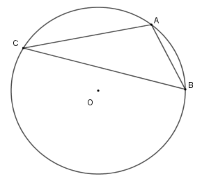
+ Vì \(AC\) bằng cạnh của hình vuông nội tiếp \(\left( O \right)\) nên số đo cung \(AC = 90^\circ \)
Vì \(BC\) bằng cạnh của tam giác đều nội tiếp \(\left( O \right)\) nên số đo cung \(BC = 120^\circ \)
Từ đó suy ra số đo cung \(AB = 120^\circ - 90^\circ = 30^\circ \)
+ Vì \(\widehat {ACB}\) là góc nội tiếp chắn cung \(AB\) nên \(\widehat {ACB} = \dfrac{{30^\circ }}{2} = 15^\circ \)
Cho \(\Delta ABC\) vuông ở $A$ . Trên cạnh $AC$ lấy điểm $M$ và vẽ đường tròn đường kính $MC$ . Kẻ $BM$ cắt đường tròn tại $D$ . Đường thẳng $DA$ cắt đường tròn tại $S$ . Chọn đáp án sai trong các đáp án sau:
-
A.
Tứ giác $ABCD$ nội tiếp.
-
B.
\(\widehat {ABD} = \widehat {ACD}\)
-
C.
$CA$ là phân giác của \(\widehat {SCB}.\)
-
D.
Tứ giác $ABCS$ nội tiếp.
Đáp án : D
Góc nội tiếp chắn nửa đường tròn là góc vuông.
Dấu hiệu nhận biết tứ giác nội tiếp:
+) Tứ giác có tổng hai góc đối diện bằng \({180^0}.\)
+) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\)
+) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác.
+) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.
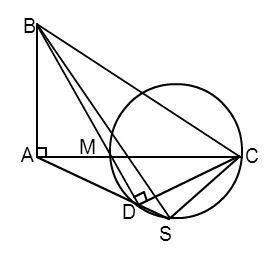
+) Ta có: \(\widehat {MDC}\) là góc nội tiếp chắn nửa đường tròn đường kính $MC$ \( \Rightarrow \widehat {MDC} = {90^0}\) (tính chất góc nội tiếp).
Xét tứ giác $ABCD$ ta có:
Góc $BAC$ và góc $BDC$ cùng nhìn đoạn $BC$ dưới góc \({90^0}.\)
\( \Rightarrow \) $ABCD$ là tứ giác nội tiếp (dhnb) \( \Rightarrow \) phương án A đúng.
+) Xét tứ giác $ABCD$ nội tiếp ta có\(\widehat {ABD} = \widehat {ACD}\) (cùng nhìn đoạn $AD$ )\( \Rightarrow \) phương án B đúng.
+) Xét đường tròn đường kính $MC$ ta có $4$ điểm $M,C,D,S$ cùng thuộc đường tròn.
\( \Rightarrow \) Tứ giác $MCSD$ là tứ giác nội tiếp.
\( \Rightarrow \widehat {ADM} = \widehat {SCM}\) (góc ngoài tại $1$ đỉnh bằng góc trong tại đỉnh đối diện). $\left( 1 \right)$
Vì tứ giác $ABCD$ nội tiếp (cmt) \( \Rightarrow \widehat {ACB} = \widehat {ADB}\) (cùng nhìn đoạn$AB$ ) $\left( 2 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)$ \( \Rightarrow \widehat {BCA} = \widehat {ACS}\;\;\;\left( { = \widehat {ADB}} \right).\)
Hay $CA$ là phân giác của \(\widehat {SCB} \Rightarrow \) phương án C đúng.
+) Giả sử tứ giác $ABCS$ là tứ giác nội tiếp \( \Rightarrow \widehat {ASB} = \widehat {BCA}\) (hai góc cùng nhìn đoạn $AB$ ).
Mà \(\widehat {ACB} = \widehat {BDA};\;\;\;\widehat {BAD} \ne \widehat {BSA}\) (xét trong đường tròn đường kính $CM$ )
\( \Rightarrow \widehat {ASB} \ne \widehat {BCA} \Rightarrow \) tứ giác $ABCS$ không là tứ giác nội tiếp \( \Rightarrow \)phương án D sai.
Ch u vi đường tròn ngoại tiếp tam giác đều cạnh \(a\,\left( {cm} \right)\) là
-
A.
$\dfrac{{4\pi a\sqrt 3 }}{3} (cm)$
-
B.
$\dfrac{{2\pi a\sqrt 3 }}{3} (cm)$
-
C.
$\dfrac{{\pi a\sqrt 3 }}{3} (cm)$
-
D.
$\dfrac{{5\pi a\sqrt 3 }}{3}(cm)$
Đáp án : B
Sử dụng công thức chu vi đường tròn bán kính \(R\) là \(C = 2\pi R\,\)
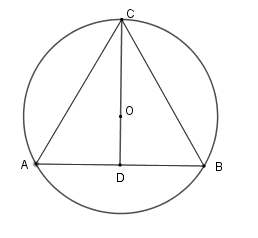
Gọi $O$ là tâm đường tròn ngoại tiếp tam giác đều \(BAC\) , suy ra \(O\) cũng là trọng tâm của tam giác \(ABC\) .
Tia \(CO \bot AB\) tại \(D\) thì $D$ là trung điểm của \(AB\) \( \Rightarrow OC = \dfrac{2}{3}CD\)
Xét tam giác vuông \(ADC\) có \(AC = a\,;\,\widehat {CAD} = 60^\circ \Rightarrow CD = AC.\sin 60^\circ = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow OC = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
Nên bán kính đường tròn ngoại tiếp tam giác \(ABC\) là \(R = \dfrac{{a\sqrt 3 }}{3} \Rightarrow C = 2\pi R = \dfrac{{2\pi a\sqrt 3 }}{3}\) .
Cho tam giác đều \(ABC\) nội tiếp đường tròn \(\left( O \right)\). Độ dài của các cung \(AB,BC,CA\) đều bằng \(4\pi \). Diện tích của tam giác đều \(ABC\) là:
-
A.
\(27\sqrt 3 \) $cm^2$
-
B.
\(7\sqrt 3 \) $cm^2$
-
C.
\(29\sqrt 3 \) $cm^2$
-
D.
\(9\sqrt 3 \) $cm^2$
Đáp án : A
+ Áp dụng công thức tính chu vi hình tròn
+ Tính chất của tam giác cân
+ Sử dụng định lý Pitago
+ Sử dụng công thức tính diện tích tam giác
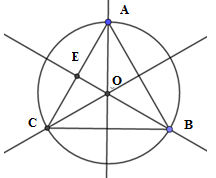
Gọi \(R\) là bán kính của đường tròn \(\left( O \right)\). Độ dài của các cung \(AB,BC,CA\) đều bằng \(4\pi \) nên ta có \(C = 2\pi R = 4\pi + 4\pi + 4\pi = 12\pi \), suy ra \(R = 6\) hay \(OA = OB = OC = 6\)
Ta cũng có \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}\) suy ra \(\Delta AOB = \Delta AOC = \Delta BOC = \dfrac{1}{3}\Delta ABC\)
Xét tam giác \(AOC\) có: \(\left\{ \begin{array}{l}\widehat {OAC} = \widehat {OCA} = {30^0}\\\widehat {COA} = {120^0}\end{array} \right.\)
Kẻ đường cao$OE$ , ta có đồng thời là đường trung tuyến, phân giác của góc \(\widehat {COA}\) . Ta có \(\widehat {AOE} = \widehat {COE} = \dfrac{1}{2}\widehat {AOC}\)
Xét tam giác $COE$ có: \(\left\{ \begin{array}{l}\widehat {ECO} = {30^0}\\\widehat {CEO} = {90^0}\end{array} \right. \Rightarrow OE = \dfrac{1}{2}CO = \dfrac{R}{2}\)
Áp dụng định lý Pytago ta có: \(CE = \sqrt {O{C^2} - O{E^2}} = \sqrt {{R^2} - {{\left( {\dfrac{R}{2}} \right)}^2}} = \dfrac{{\sqrt 3 }}{2}R\)
Vậy \({S_{COE}} = \dfrac{1}{2}OE.CE = \dfrac{1}{2}.\dfrac{R}{2}.\dfrac{{\sqrt 3 R}}{2} = \dfrac{{\sqrt 3 {R^2}}}{8}\)
Suy ra \({S_{COA}} = 2{S_{COE}} = \dfrac{{\sqrt 3 {R^2}}}{4}\) và \({S_{ABC}} = 3{S_{COA}} = \dfrac{{3\sqrt 3 {R^2}}}{4} = \dfrac{{3\sqrt 3 {R^2}}}{4} = 27\sqrt 3 \,\ cm^2 .\)
Từ điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(MA, MB\) với \(\left( O \right)\) tại \(A\) và \(B.\) Qua \(A\) vẽ đường thẳng song song với \(MB\) cắt đường tròn tại \(C.\)

Nối \(C\) với \(M\) cắt đường tròn \(\left( O \right)\) tại \(D.\) Nối \(A\) với \(D\) cắt \(MB\) tại \(E.\) Chọn câu đúng
-
A.
\(ME = 2EB\)
-
B.
\(2ME = EB\)
-
C.
\(ME = EB.\)
-
D.
\(3ME = 2EB\)
Đáp án : C
Sử dụng tính chất góc nội tiếp và góc giữa tiếp tuyến và dây cung cùng chắn 1 cung.
Sử dụng tính chất tam giác đồng dạng.
Xét \(\Delta ABE\) và \(\Delta BDE\) có:
+ \(\widehat E\) chung.
+ \(\widehat {BAE} = \widehat {DBE}\) (góc nội tiếp và góc giữa tia tiếp tuyến và dây cung cùng chắn cung $BD$ )
Do đó ta có \(\Delta ABE \backsim \Delta BDE\,\left( {g.g} \right)\).
\( \Rightarrow \dfrac{{AE}}{{BE}} = \dfrac{{BE}}{{DE}} \Rightarrow E{B^2} = AE.DE\,\,\left( 1 \right).\)
Ta có: \(MB//AC \Rightarrow \widehat {EMD} = \widehat {DCA}\) (hai góc so le trong)
Mà \(\widehat {DCA} = \widehat {MAD}\) (góc nội tiếp và góc giữa tiếp tuyến và dây cung cùng chắn cung \(AD\))
Do đó \(\widehat {EMD} = \widehat {MAD}\).
Xét \(\Delta MEA\) và \(\Delta DEM\) có:
\(\widehat E\) chung.
\(\widehat {EMD} = \widehat {MAD}\) (cmt)
Suy ra \(\Delta MEA \backsim \Delta DEM\,.\)
Do đó
\(\dfrac{{ME}}{{DE}} = \dfrac{{EA}}{{EM}} \Rightarrow M{E^2} = DE.EA\,\,\left( 2 \right).\)
Từ \(\left( 1 \right)\) và \(2\) ta nhận được \(E{B^2} = E{M^2} \Rightarrow EB = EM.\)
Cho \(A\) là điểm cố định trên đường tròn \(\left( {O;R} \right).\) Gọi \(AB\) và \(AC\) là hai dây cung thay đổi trên đường tròn \(\left( O \right)\) thỏa mãn \(\sqrt {AB.AC} = R\sqrt 3 .\) Khi đó vị trí của \(B,\,C\) trên \(\left( O \right)\) để diện tích \(\Delta ABC\) lớn nhất là:
-
A.
\(\Delta ABC\) cân
-
B.
\(\Delta ABC\) đều.
-
C.
\(\Delta ABC\) vuông cân
-
D.
\(\Delta ABC\) vuông
Đáp án : B
Kẻ \(AH \bot BC,\,OI \bot BC\), đường kính $AD.$
Sử dụng tính chất góc nội tiếp chắn nửa đường tròn để chứng minh \(\widehat {ABD} = {90^0} \Rightarrow \Delta ABD \backsim \Delta AHC\).
Tính độ dài \(AH\) từ tính chất hai tam giác đồng dạng, từ đó suy ra điều kiện để diện tích tam giác \(ABC\) lớn nhất.
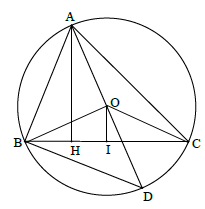
Kẻ \(AH \bot BC,\,OI \bot BC\), đường kính $AD.$
Ta chứng minh được \(\Delta AHC \backsim \Delta ABD\,\left( {g - g} \right).\)
Do đó \(\dfrac{{AH}}{{AB}} = \dfrac{{AC}}{{AD}} \Rightarrow AH.AD = AB.AC \)\(\Rightarrow AB.AC = 2R.AH\,\,\left( 1 \right).\)
Theo giả thiết \(\sqrt {AB.AC} = R\sqrt 3 ,\) nên \(AB.AC = 3{R^2}\,\,\left( 2 \right).\)
Thay \(\left( 2 \right)\) và \(\left( 1 \right)\) ta có \(AH = \dfrac{{3R}}{2}.\)
Lại có \(OI + OA \ge AI \ge AH\) nên \(OI \ge AH - OA = \dfrac{{3R}}{2} - R = \dfrac{R}{2}.\)
Do \(AH = \dfrac{{3R}}{2}\) là giá trị không đổi nên \({S_{ABC}}\) lớn nhất khi \(BC\) lớn nhất \( \Leftrightarrow OI\) nhỏ nhất
\( \Leftrightarrow OI = \dfrac{R}{2} \Leftrightarrow BC \bot OA \Rightarrow \Delta ABC\) cân tại \(A\).
Mà \(OI = \dfrac{R}{2} \Rightarrow \sin \widehat {OBI} \)\(= \dfrac{{OI}}{{OB}} = \dfrac{1}{2}\)\( \Rightarrow \widehat {OBI} = \widehat {OCI} = {30^0} \)\(\Rightarrow \widehat {BOC} \)\(= {120^0}\)$ \Rightarrow \widehat {BAC} = {60^0}$
Vậy \(\Delta ABC\) đều.