Đề kiểm tra giữa học kì 2 Toán 9 - Đề số 1
Đề bài
Phương trình nào dưới đây nhận cặp số $\left( { - 2;4} \right)$ làm nghiệm
-
A.
$x - 2y = 0$
-
B.
$2x + y = 0$
-
C.
$x - y = 2$
-
D.
$x + 2y + 1 = 0$
Hệ phương trình \(\left\{ \begin{array}{l}x\sqrt 2 - y\sqrt 3 = 1\\x + y\sqrt 3 = \sqrt 2 \end{array} \right.\) có bao nhiêu nghiệm?
-
A.
$1$
-
B.
$0$
-
C.
$2$
-
D.
Vô số.
Kết luận nào sau đây là sai khi nói về đồ thị của hàm số $y = a{x^2}\,\,$ với $a \ne 0$.
-
A.
Đồ thị hàm số nhận trục tung làm trục đối xứng
-
B.
Với $a > 0$ đồ thị nằm phía trên trục hoành và $O$ là điểm cao nhất của đồ thị
-
C.
Với $a < 0$ đồ thị nằm phía dưới trục hoành và $O$ là điểm cao nhất của đồ thị
-
D.
Với $a > 0$ đồ thị nằm phía trên trục hoành và $O$ là điểm thấp nhất của đồ thị
Có bao nhiêu phương trình trong các phương trình dưới đây là phương trình bậc hai một ẩn
\(\sqrt 2 {x^2} + 1 = 0\); \({x^2} + 2019x = 0\) ; \(x + \sqrt x - 1 = 0\) ; \(2x + 2{y^2} + 3 = 9\); \(\dfrac{1}{{{x^2}}} + x + 1 = 0\)
-
A.
\(2\)
-
B.
\(3\)
-
C.
\(4\)
-
D.
\(0\)
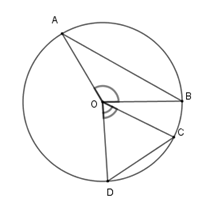
Cho tam giác $ABC$ đều nội tiếp đường tròn $\left( O \right)$. Tính số đo cung $AC$ lớn.
-
A.
$240^\circ $
-
B.
$120^\circ $
-
C.
$360^\circ $
-
D.
$210^\circ $
Cặp số \(\left( {3; - 5} \right)\) là nghiệm của hệ phương trình nào sau đây?
-
A.
\(\left\{ \begin{array}{l}x - 3y = 1\\x + y = 2\end{array} \right.\)
-
B.
$\left\{ \begin{array}{l}3x + y = 4\\2x - y = 11\end{array} \right.$
-
C.
$\left\{ \begin{array}{l}y = - 1\\x - 3y = 5\end{array} \right.$
-
D.
$\left\{ \begin{array}{l}4x - y = 0\\x - 3y = 0\end{array} \right.$
“Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi… Tia nối từ tâm tới điểm đó là tia phân giác của góc tạo bởi…” Hai cụm từ thích hợp vào chỗ trống lần lượt là
-
A.
hai tiếp tuyến, hai bán kính đi qua tiếp điểm
-
B.
hai bán kính đi qua tiếp điểm, hai tiếp tuyến
-
C.
hai tiếp tuyến, hai dây cung
-
D.
hai dây cung, hai bán kính
B iết hệ phương trình: $\left\{ \begin{array}{l}2x + by = a\\bx + ay = 5\end{array} \right.$ có nghiệm $x = 1$ ; $y = 3.$ Tính $10\left( {a + b} \right)$
-
A.
$15$
-
B.
$16$
-
C.
$14$
-
D.
$17$
Cho hai đường tròn $\left( {O;8\,cm} \right)$ và $\left( {O';6cm} \right)$ cắt nhau tại $A,B$ sao cho $OA$ là tiếp tuyến của $\left( {O'} \right)$. Độ dài dây $AB$ là
-
A.
$AB = 8,6\,cm$
-
B.
$AB = 6,9\,cm$
-
C.
$AB = 4,8\,cm$
-
D.
$AB = 9,6\,cm$
Cho một số có hai chữ số . Chữ số hàng chục lớn hơn chữ số hàng đơn vị là $5$. Nếu đổi chỗ hai chữ số cho nhau ta được một số bằng $\dfrac{3}{8}$ số ban đầu. Tìm tích các chữ số của số ban đầu.
-
A.
$12$
-
B.
$16$
-
C.
$14$
-
D.
$6$
Chọn khẳng định đúng. Góc ở tâm là góc
-
A.
Có đỉnh nằm trên đường tròn
-
B.
Có đỉnh trùng với tâm đường tròn
-
C.
Có hai cạnh là hai đường kính của đường tròn
-
D.
Có đỉnh nằm trên bán kính của đường tròn
Cho phương trình $ax + by = c$ với $a \ne 0;b \ne 0$. Chọn câu đúng nhất.
-
A.
Phương trình đã cho luôn có vô số nghiệm.
-
B.
Tập nghiệm của phương trình được biểu diễn bởi đường thẳng $d:{\rm{ }}ax + by = c.$
-
C.
Tập nghiệm của phương trình là \(S = \left\{ {\left( {x;\dfrac{{ - a}}{b}x + \dfrac{c}{b}} \right)|x \in \mathbb{R}} \right\}\)
-
D.
Cả A, B, C đều đúng
Không dùng công thức nghiệm, tìm số nghiệm của phương trình $ - 4{x^2} + 9 = 0$.
-
A.
$0$
-
B.
$1$
-
C.
$3$
-
D.
$2$
Xác định giá trị của tham số $m$ để hệ phương trình \(\left\{ \begin{array}{l}x + y = - 1\\mx + y = 2m\end{array} \right.\) vô nghiệm.
-
A.
$m = 1$
-
B.
$m = - 1$
-
C.
$m = 0$
-
D.
$m = \dfrac{1}{2}$
Cho hệ phương trình \(\left\{ \begin{array}{l}8x + 7y = 16\\8x - 3y = - 24\end{array} \right.\) . Nghiệm của hệ phương trình là
-
A.
$\left( {x;y} \right) = \left( { - \dfrac{3}{2};4} \right)$
-
B.
$\left( {x;y} \right) = \left( {4; - \dfrac{3}{2}} \right)$
-
C.
$\left( {x;y} \right) = \left( { - \dfrac{3}{2}; - 4} \right)$
-
D.
$\left( {x;y} \right) = \left( { - 2;2} \right)$
Tính $\Delta '$ và tìm số nghiệm của phương trình \(7{x^2} - 12x + 4 = 0\) .
-
A.
$\Delta ' = 6$ và phương trình có hai nghiệm phân biệt
-
B.
$\Delta ' = 8$ và phương trình có hai nghiệm phân biệt
-
C.
$\Delta ' = 8$ và phương trình có nghiệm kép
-
D.
$\Delta ' = 0$ và phương trình có hai nghiệm phân biệt
Một ô tô đi quãng đường $AB$ với vận tốc $50\,\,km/h$ , rồi đi tiếp quãng đường $BC$ với vận tốc $45km/h.$ Biết quãng đường tổng cộng dài $165\,\,km$ và thời gian ô tô đi trên quãng đường $AB$ ít hơn thời gian đi trên quãng đường $BC$ là $30$ phút. Tính thời gian ô tô đi trên đoạn đường $AB$.
-
A.
$2$ giờ
-
B.
$1,5$ giờ
-
C.
$1$ giờ
-
D.
$3$ giờ
Cho hệ phương trình $\left\{ \begin{array}{l}x - y = 5\\3x + 2y = 18\end{array} \right.$có nghiệm $\left( {x;y} \right)$. Tích $x.y$ là
-
A.
$5$
-
B.
$\dfrac{84}{25}$
-
C.
$\dfrac{25}{84}$
-
D.
$\dfrac{84}{5}$
Cho hàm số $y = f\left( x \right) = \left( { - 2m + 1} \right){x^2}.$
Tìm giá trị của $m$ để đồ thị đi qua điểm $A\left( { - 2;4} \right).$
-
A.
$m = 0$
-
B.
$m = 1$
-
C.
$m = 2$
-
D.
$m = - 2$
Cho đường tròn $(O)$ đường kính $AB$ và một cung $AC$ có số đo nhỏ hơn $90^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai ?
-
A.
$AC = BE$
-
B.
Số đo cung$AD$ bằng số đo cung $BE$
-
C.
Số đo cung $AC$ bằng số đo cung $BE$
-
D.
$\widehat {AOC} < \widehat {AOD}$
Cho đường thẳng $d$ có phương trình $(2m - 4)x + (m - 1)y = m - 5$
Tìm các giá trị của tham số m để $d$ đi qua gốc tọa độ.
-
A.
$m = 2$
-
B.
$m = 1$
-
C.
$m = 5$
-
D.
$m \ne 5$
Xác định giá trị của tham số $m$ để hệ phương trình \(\left\{ \begin{array}{l}x - \left( {m - 2} \right)y = 2\\\left( {m - 1} \right)x - 2y = m - 5\end{array} \right.\) có nghiệm duy nhất
-
A.
$m \ne 0$
-
B.
$m \ne 2$
-
C.
$m \ne \left\{ {0;3} \right\}$
-
D.
$m = 0;m = 3$
Kết luận nào đúng khi nói về nghiệm $\left( {x;y} \right)$ của hệ phương trình \(\left\{ \begin{array}{l}x + \dfrac{y}{2} = \dfrac{{2x - 3}}{2}\\\dfrac{x}{2} + 3y = \dfrac{{25 - 9y}}{8}\end{array} \right.\)
-
A.
$x > 0;y < 0$
-
B.
$x < 0;y < 0$
-
C.
$x < 0;y > 0$
-
D.
$x > 0;y > 0$
Cho hệ phương trình $\left\{ \begin{array}{l}x + 2y = m + 3\\2x - 3y = m\end{array} \right.$ ( $m$ là tham số) . Tìm $m$ để hệ có nghiệm duy nhất $\left( {x,y} \right)$ thỏa mãn $x + y = - 3$.
-
A.
$m = - 6$
-
B.
$m = 6$
-
C.
$m = 3$
-
D.
$m = - 4$
Hai trường có tất cả 300 học sinh tham gia một cuộc thi. Biết trường A có $75\% $ học sinh đạt, trường 2 có $60\% $ đạt nên cả 2 trường có 207 học sinh đạt. Số học sinh dự thi của trường A và trường B lần lượt là:
-
A.
160 và 140
-
B.
200 và 100
-
C.
180 và 120
-
D.
Tất cả đều sai
Cho hàm số \(y = - \dfrac{2}{5}{x^2}\,\,\)có đồ thị là \((P)\). Điểm trên \(\left( P \right)\) (khác gốc tọa độ \(O\left( {0;0} \right)\)) có tung độ gấp ba lần hoành độ thì có hoành độ là:
-
A.
\(\dfrac{{15}}{2}\)
-
B.
\(\dfrac{{ - 15}}{2}\)
-
C.
\(\dfrac{2}{{15}}\)
-
D.
\( - \dfrac{2}{{15}}\)
Tìm điều kiện của tham số m để phương trình \(2{x^2} + 5x + m - 1 = 0\) vô nghiệm
-
A.
\(m > \dfrac{8}{{33}}\)
-
B.
Không tồn tại \(m\)
-
C.
\(m < \dfrac{{33}}{8}\)
-
D.
\(m > \dfrac{{33}}{8}\)
Cho phương trình \((m - 2){x^2} - 2(m + 1)x + m = 0\). Tìm các giá trị của $m$ để phương trình có một nghiệm
-
A.
$m = - 2$
-
B.
$m = 2;m = - \dfrac{1}{4}$
-
C.
$m = - \dfrac{1}{4}$
-
D.
$m \ne 2$
Cho đường tròn $(O).$ Từ một điểm $M$ ở ngoài $(O)$, vẽ hai tiếp tuyến $MA$ và $MB$ sao cho góc $AMB$ bằng ${120^0}$. Biết chu vi tam giác $MAB$ là $6\left( {3 + 2\sqrt 3 } \right)cm$, tính độ dài dây $AB.$
-
A.
$18\,cm$
-
B.
$6\sqrt 3 cm$
-
C.
$12\sqrt 3 \,cm$
-
D.
$15\,cm$
Cho hai đường tròn $\left( {O;20cm} \right)$ và $\left( {O';15cm} \right)$ cắt nhau tại $A$ và$B$. Tính đoạn nối tâm $OO'$, biết rằng$AB = 24cm$ và $O$ và $O'$ nằm cùng phía đối với $AB$ .
-
A.
$OO' = 7cm$
-
B.
$OO' = 8cm$
-
C.
$OO' = 9cm$
-
D.
$OO' = 25cm$
Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\)tiếp xúc ngoài tại \(A\). Kẻ các đường kính \(AOB;AO'C\). Gọi \(DE\) là tiếp tuyến chung của hai đường tròn \(\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)\). Gọi \(M\) là giao điểm của \(BD\) và \(CE\). Tính diện tích tứ giác \(ADME\) biết \(\widehat {DOA} = 60^\circ \) và \(OA = 8\,cm\)
-
A.
\(12\sqrt 3 \,\,c{m^2}\)
-
B.
\( \dfrac{64}{3}\sqrt 3 \,\,c{m^2}\)
-
C.
\( \dfrac{32}{3}\sqrt 3 \,\,c{m^2}\)
-
D.
\(36\,\,c{m^2}\)
Cho đường tròn \(\left( O \right)\) đường kính \(AB,\) vẽ góc ở tâm \(\widehat {AOC} = 60^\circ \) . Vẽ dây \(CD\) vuông góc với \(AB\) và dây \(DE\) song song với \(AB.\) Tính số đo cung nhỏ \(BE\)
-
A.
$120^\circ $
-
B.
$60^\circ $
-
C.
$240^\circ $
-
D.
$30^\circ $
Cho tam giác $ABC$ cân tại $A$ và $\widehat A = 66^\circ $ nội tiếp đường tròn $\left( O \right)$. Trong các cung nhỏ $AB;BC;AC$, cung nào là cung lớn nhất?
-
A.
$AB$
-
B.
$AC$
-
C.
$BC$
-
D.
$AB,AC$
Cho đường tròn $\left( {O;R} \right)$ và hai dây $AB;CD$ sao cho $\widehat {AOB} = 120^\circ ;\widehat {COD} = 60^\circ $. So sánh các dây $CD;AB$.
-
A.
$CD = 2AB$
-
B.
$AB > 2CD$
-
C.
$CD > AB$
-
D.
$CD < AB < 2CD$
Cho tam giác $ABC$ có \(AB = 5cm;AC = 3cm\) thuộc đường tròn tâm $(O),$ đường cao $AH$, đường kính $AD.$ Khi đó tích $AH.AD$ bằng
-
A.
\(15c{m^2}\)
-
B.
$8c{m^2}$
-
C.
\(12c{m^2}\)
-
D.
$30c{m^2}$
Cho tam giác ABC nằm trên đường tròn $(O;R), $đường cao $AH,$ biết $AB = 9{\rm{ }}cm,$ $AC = 12{\rm{ }}cm,$ $AH = 4{\rm{ }}cm.$ Tính bán kính của đường tròn $(O)$.
-
A.
\(13,5\,cm\)
-
B.
$12\,cm$
-
C.
\(18\,cm\)
-
D.
$6\,cm$
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) có \(AC = 3cm\) . Kẻ tiếp tuyến \(xAy\) với \(\left( O \right)\) . Từ \(C\) kẻ \(CM{\rm{//}}xy\left( {M \in AB} \right)\) . Chọn câu đúng.
-
A.
\(AM.AB = 12c{m^2}\)
-
B.
\(AM.AB = 6c{m^2}\)
-
C.
\(AM.AB = 9c{m^2}\)
-
D.
\(AM.AB = B{C^2}\)
Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$ cắt nhau tại $A$ và $B$. Một đường thẳng tiếp xúc với $\left( O \right)$ tại $C$, và tiếp xúc với đường tròn $\left( {O'} \right)$ tại $D$ sao cho tia \(AB\) cắt đoạn \(CD\). Vẽ đường tròn $\left( I \right)$ đi qua ba điểm $A,C,D$ cắt đường thẳng $AB$ tại một điểm thứ hai là $E$. Chọn câu đúng:
-
A.
Tứ giác $BCED$ là hình thoi
-
B.
Tứ giác $BCED$ là hình bình hành
-
C.
Tứ giác $BCED$ là hình vuông
-
D.
Tứ giác $BCED$ là hình chữ nhật
Tìm \(m\) để hai phương trình \({x^2} + mx + 2 = 0\) và \({x^2} + 2x + m = 0\) có ít nhất một nghiệm chung.
-
A.
\(1\)
-
B.
\( - 3\)
-
C.
\( - 1\)
-
D.
\(3\)
Cho đường thẳng xy và đường tròn (O; R) không giao nhau. Gọi M là một điểm di động trên xy. Vẽ đường tròn đường kính OM cắt đường tròn (O) tại A và B. Kẻ \(OH \bot xy\) . Chọn câu đúng.
-
A.
Đường thẳng AB luôn đi qua một điểm cố định là \(H.\)
-
B.
Đường thẳng AB luôn đi qua một điểm cố định là trung điểm \(OH\) .
-
C.
Đường thẳng AB luôn đi qua một điểm cố định là giao của \(OH\) và \(AB.\)
-
D.
Đường thẳng AB luôn đi qua một điểm cố định là giao của \(OH\) và \(\left( {O;R} \right).\)
Lời giải và đáp án
Phương trình nào dưới đây nhận cặp số $\left( { - 2;4} \right)$ làm nghiệm
-
A.
$x - 2y = 0$
-
B.
$2x + y = 0$
-
C.
$x - y = 2$
-
D.
$x + 2y + 1 = 0$
Đáp án : B
Nếu cặp số thực $({x_0},\,{y_0})$ thỏa mãn ${\rm{ax}} + by = c$ thì nó được gọi là nghiệm của phương trình $ax + by = c$.
Thay $x = - 2;y = 4$ vào từng phương trình ta được
+) $x - 2y = - 2 - 2.4 = - 10 \ne 0$ nên loại A.
+) $x - y = - 2 - 4 = - 6 \ne 0$ nên loại C.
+) $x + 2y + 1 = - 2 + 2.4 + 1 = 7 \ne 0$ nên loại D.
+) $2x + y = - 2.2 + 4 = 0$ nên chọn B.
Hệ phương trình \(\left\{ \begin{array}{l}x\sqrt 2 - y\sqrt 3 = 1\\x + y\sqrt 3 = \sqrt 2 \end{array} \right.\) có bao nhiêu nghiệm?
-
A.
$1$
-
B.
$0$
-
C.
$2$
-
D.
Vô số.
Đáp án : A
Giải hệ phương trình bằng phương pháp thế
Rút \(x\) từ phương trình thứ hai thay vào phương trình thứ nhất để tìm \(x\), từ đó tìm được \(y.\)
Ta có \(\left\{ \begin{array}{l}x\sqrt 2 - y\sqrt 3 = 1\\x + y\sqrt 3 = \sqrt 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {\sqrt 2 - y\sqrt 3 } \right)\sqrt 2 - y\sqrt 3 = 1\\x = \sqrt 2 - y\sqrt 3 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 - y\left( {\sqrt 6 + \sqrt 3 } \right) = 1\\x = \sqrt 2 - y\sqrt 3 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y\left( {\sqrt 6 + \sqrt 3 } \right) = 1\\x = \sqrt 2 - y\sqrt 3 \end{array} \right.\)$ \Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{{\sqrt 6 - \sqrt 3 }}{3}\\x = \sqrt 2 - y\sqrt 3 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{{\sqrt 6 - \sqrt 3 }}{3}\\x = 1\end{array} \right.$
Vậy hệ phương trình đã cho có nghiệm duy nhất \(\left( {x;y} \right) = \left( {1;\dfrac{{\sqrt 6 - \sqrt 3 }}{3}} \right)\)
Kết luận nào sau đây là sai khi nói về đồ thị của hàm số $y = a{x^2}\,\,$ với $a \ne 0$.
-
A.
Đồ thị hàm số nhận trục tung làm trục đối xứng
-
B.
Với $a > 0$ đồ thị nằm phía trên trục hoành và $O$ là điểm cao nhất của đồ thị
-
C.
Với $a < 0$ đồ thị nằm phía dưới trục hoành và $O$ là điểm cao nhất của đồ thị
-
D.
Với $a > 0$ đồ thị nằm phía trên trục hoành và $O$ là điểm thấp nhất của đồ thị
Đáp án : B
Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một parabol đi qua gốc tọa độ $O,$ nhận $Oy$ là trục đối xứng ($O$ là đỉnh của parabol).
- Nếu \(a > 0\) thì đồ thị nằm phía trên trục hoành, $O$ là điểm thấp nhất của đồ thị.
- Nếu \(a < 0\) thì đồ thị nằm phía dưới trục hoành, $O$ là điểm cao nhất của đồ thị.
Có bao nhiêu phương trình trong các phương trình dưới đây là phương trình bậc hai một ẩn
\(\sqrt 2 {x^2} + 1 = 0\); \({x^2} + 2019x = 0\) ; \(x + \sqrt x - 1 = 0\) ; \(2x + 2{y^2} + 3 = 9\); \(\dfrac{1}{{{x^2}}} + x + 1 = 0\)
-
A.
\(2\)
-
B.
\(3\)
-
C.
\(4\)
-
D.
\(0\)
Đáp án : A
Sử dụng định nghĩa phương trình bậc hai một ẩn.
Phương trình bậc hai một ẩn ( hay gọi tắt là phương trình bậc hai) là phương trình có dạng:
\(a{x^2} + bx + c = 0\,\,(a \ne 0)\) trong đó \(a,b,c\) là các số thực cho trước, \(x\) là ẩn số.
- Phương trình \(x + \sqrt x - 1 = 0\) có chứa căn thức nên không là phương trình bậc hai một ẩn.
- Phương trình \(2x + 2{y^2} + 3 = 9\) có chứa hai biến \(x;y\) nên không là phương trình bậc hai một ẩn.
- Phương trình \(\dfrac{1}{{{x^2}}} + x + 1 = 0\) có chứa ẩn ở mẫu thức nên không là phương trình bậc hai một ẩn.
- Phương trình \(\sqrt 2 {x^2} + 1 = 0\) và \({x^2} + 2019x = 0\) là những phương trình bậc hai một ẩn.
Vậy có hai phương trình bậc hai một ẩn trong số các phương trình đã cho.
Cho tam giác $ABC$ đều nội tiếp đường tròn $\left( O \right)$. Tính số đo cung $AC$ lớn.
-
A.
$240^\circ $
-
B.
$120^\circ $
-
C.
$360^\circ $
-
D.
$210^\circ $
Đáp án : A
Sử dụng định lý tổng các góc trong tam giác và số đo cung.
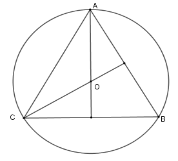
Vì tam giác $ABC$ đều có $O$ là tâm đường tròn ngoại tiếp nên $O$ cũng là giao ba đường phân giác nên $AO;CO$ lần lượt là các đường phân giác $\widehat {BAC}$; $\widehat {ACB}$.
Ta có $\widehat {CAO} = \dfrac{1}{2}\widehat {BAC} = \dfrac{{60^\circ }}{2} = 30^\circ $;$\widehat {ACO} = \dfrac{1}{2}\widehat {ACB} = \dfrac{{60^\circ }}{2} = 30^\circ $
Xét tam giác $AOC$ có $\widehat {AOC} = 180^\circ - \widehat {CAO} - \widehat {ACO} = 120^\circ $ nên số đo cung nhỏ $AC$ là $120^\circ $.
Do đó số đo cung lớn $AC$ là $360^\circ - 120^\circ = 240^\circ $.
Cặp số \(\left( {3; - 5} \right)\) là nghiệm của hệ phương trình nào sau đây?
-
A.
\(\left\{ \begin{array}{l}x - 3y = 1\\x + y = 2\end{array} \right.\)
-
B.
$\left\{ \begin{array}{l}3x + y = 4\\2x - y = 11\end{array} \right.$
-
C.
$\left\{ \begin{array}{l}y = - 1\\x - 3y = 5\end{array} \right.$
-
D.
$\left\{ \begin{array}{l}4x - y = 0\\x - 3y = 0\end{array} \right.$
Đáp án : B
Cặp số \(\left( {{x_0};{y_0}} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) khi và chỉ khi nó thỏa mãn cả hai phương trình của hệ.
+) Thay $x = 3;y = - 5$ vào hệ \(\left\{ \begin{array}{l}x - 3y = 1\\x + y = 2\end{array} \right.\) ta được \(\left\{ \begin{array}{l}3 - 3\left( { - 5} \right) = 1\\3 + \left( { - 5} \right) = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}18 = 1\\ - 2 = 2\end{array} \right.\) (vô lý) nên loại A.
+) Thay $x = 3;y = - 5$ vào hệ $\left\{ \begin{array}{l}y = - 1\\x - 3y = 5\end{array} \right.$ ta được $\left\{ \begin{array}{l} - 5 = - 1\\3 - 3.\left( { - 5} \right) = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 5 = - 1\\18 = 5\end{array} \right.$ (vô lý) nên loại C.
+) Thay $x = 3;y = - 5$ vào hệ $\left\{ \begin{array}{l}4x - y = 0\\x - 3y = 0\end{array} \right.$ ta được $\left\{ \begin{array}{l}4.3 - \left( { - 5} \right) = 0\\3 - 3.\left( { - 5} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}17 = 0\\18 = 0\end{array} \right.$ (vô lý) nên loại D.
+) Thay $x = 3;y = - 5$ vào hệ $\left\{ \begin{array}{l}3x + y = 4\\2x - y = 11\end{array} \right.$ ta được $\left\{ \begin{array}{l}3.3 + \left( { - 5} \right) = 4\\2.3 - \left( { - 5} \right) = 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4 = 4\\11 = 11\end{array} \right.$ (luôn đúng) nên chọn B.
“Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi… Tia nối từ tâm tới điểm đó là tia phân giác của góc tạo bởi…” Hai cụm từ thích hợp vào chỗ trống lần lượt là
-
A.
hai tiếp tuyến, hai bán kính đi qua tiếp điểm
-
B.
hai bán kính đi qua tiếp điểm, hai tiếp tuyến
-
C.
hai tiếp tuyến, hai dây cung
-
D.
hai dây cung, hai bán kính
Đáp án : A
Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:
- Điểm đó cách đều hai tiếp điểm.
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của các góc tạo bởi hai tiếp tuyến.
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.
B iết hệ phương trình: $\left\{ \begin{array}{l}2x + by = a\\bx + ay = 5\end{array} \right.$ có nghiệm $x = 1$ ; $y = 3.$ Tính $10\left( {a + b} \right)$
-
A.
$15$
-
B.
$16$
-
C.
$14$
-
D.
$17$
Đáp án : B
-Thay $x;y$ vào hệ phương trình ta được hệ phương trình mới ẩn $a,b$.
-Giải hệ phương trình mới bằng phương pháp cộng đại số hoặc phương pháp thế ta tìm được $a,b$
Thay $x = 1$; $y = 3$ vào hệ ta có:
$\left\{ \begin{array}{l}2.1 + b.3 = a\\b.1 + a.3 = 5\end{array} \right.$$ \Leftrightarrow $$\left\{ \begin{array}{l}a - 3b = 2\\3a + b = 5\end{array} \right.$$ \Leftrightarrow $$\left\{ \begin{array}{l}3a - 9b = 6\\3a + b = 5\end{array} \right.$$ \Leftrightarrow $$\left\{ \begin{array}{l}10b = - 1\\3a + b = 5\end{array} \right.$$ \Leftrightarrow $$\left\{ \begin{array}{l}b = \dfrac{{ - 1}}{{10}}\\a = \dfrac{{17}}{{10}}\end{array} \right.$ .
Vậy $a = \dfrac{{ - 1}}{{10}}$; $y = \dfrac{{17}}{{10}}$ thì hệ phương trình có nghiệm $x = 1$; $y = 3.$
$ \Rightarrow 10\left( {a + b} \right) = 16$
Cho hai đường tròn $\left( {O;8\,cm} \right)$ và $\left( {O';6cm} \right)$ cắt nhau tại $A,B$ sao cho $OA$ là tiếp tuyến của $\left( {O'} \right)$. Độ dài dây $AB$ là
-
A.
$AB = 8,6\,cm$
-
B.
$AB = 6,9\,cm$
-
C.
$AB = 4,8\,cm$
-
D.
$AB = 9,6\,cm$
Đáp án : D
Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và hệ thức lượng trong tam giác vuông.
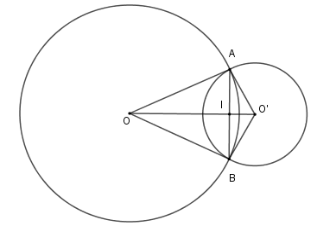
Vì $OA$ là tiếp tuyến của $\left( {O'} \right)$ nên $\Delta OAO'$ vuông tại $A$.
Vì $\left( O \right)$ và $\left( {O'} \right)$ cắt nhau tại $A,B$ nên đường nối tâm $OO'$ là trung trực của đoạn $AB$.
Gọi giao điểm của $AB$ và $OO'$ là $I$ thì $AB \bot OO'$ tại $I$ là trung điểm của $AB$
Áp dụng hệ thức lượng trong tam giác vuông $OAO'$ ta có
$\dfrac{1}{{A{I^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O'{A^2}}} = \dfrac{1}{{{8^2}}} + \dfrac{1}{{{6^2}}} \Rightarrow AI = 4,8\,cm \Rightarrow AB = 9,6\,cm$
Cho một số có hai chữ số . Chữ số hàng chục lớn hơn chữ số hàng đơn vị là $5$. Nếu đổi chỗ hai chữ số cho nhau ta được một số bằng $\dfrac{3}{8}$ số ban đầu. Tìm tích các chữ số của số ban đầu.
-
A.
$12$
-
B.
$16$
-
C.
$14$
-
D.
$6$
Đáp án : C
Gọi số cần tìm là \(\overline {ab} ,\,\,a \in {\mathbb{N}^*},\,\,b \in {\mathbb{N}^*}\), $a,b \le 9$.
Biểu diễn số mới theo ab, từ đó viết các phương trình dựa vào đề bài để lập hệ phương trình.
Sử dụng phương pháp thế để giải hệ phương trình tìm được.
Gọi số cần tìm là \(\overline {ab} ,\,\,a \in {\mathbb{N}^*},\,\,b \in {\mathbb{N}^*}\), $a,b \le 9$.
Đổi chỗ hai chữ số của nó thì được một số mới là \(\overline {ba} \)
Ta có hệ phương trình: $\left\{ \begin{array}{l}a - b = 5\\\overline {ba} = \dfrac{3}{8}\overline {ab} \end{array} \right.$ hay $\left\{ \begin{array}{l}a - b = 5 \;(1)\\b.10 + a = \dfrac{3}{8}\left( {a.10 + b} \right) (2)\end{array}\right.$
Nhân cả hai vế của phương trình (2) với 8, ta được phương trình: \(80b + 8a = 30a + 3b \;(3)\)
Từ phương trình (1) suy ra $a = b + 5$
Thế vào phương trình (3), ta được:
$80b + 8\left( {b + 5} \right) = 30\left( {b + 5} \right) + 3b$
$55b = 110$
$b = 2$ (TM)
Suy ra $a = 2 + 5 = 7$ (TM)
Vậy số cần tìm là $72$ nên tích các chữ số là $2.7 = 14$.
Chọn khẳng định đúng. Góc ở tâm là góc
-
A.
Có đỉnh nằm trên đường tròn
-
B.
Có đỉnh trùng với tâm đường tròn
-
C.
Có hai cạnh là hai đường kính của đường tròn
-
D.
Có đỉnh nằm trên bán kính của đường tròn
Đáp án : B
Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
Cho phương trình $ax + by = c$ với $a \ne 0;b \ne 0$. Chọn câu đúng nhất.
-
A.
Phương trình đã cho luôn có vô số nghiệm.
-
B.
Tập nghiệm của phương trình được biểu diễn bởi đường thẳng $d:{\rm{ }}ax + by = c.$
-
C.
Tập nghiệm của phương trình là \(S = \left\{ {\left( {x;\dfrac{{ - a}}{b}x + \dfrac{c}{b}} \right)|x \in \mathbb{R}} \right\}\)
-
D.
Cả A, B, C đều đúng
Đáp án : D
Phương trình bậc nhất hai ẩn ${\rm{ax}} + by = c$ luôn có vô số nghiệm.
Tập nghiệm của phương trình được biểu diễn bởi đường thẳng $d:{\rm{ }}ax + by = c.$
Ta có với $a \ne 0,b \ne 0$ thì
$ax + by = c\\ by = - ax + c\\y = - \dfrac{a}{b}x + \dfrac{c}{b}$
Nghiệm của phương trình là \(S = \left\{ {\left( {x;\dfrac{{ - a}}{b}x + \dfrac{c}{b}} \right)|x \in \mathbb{R}} \right\}\)
Vậy cả A, B, C đều đúng.
Không dùng công thức nghiệm, tìm số nghiệm của phương trình $ - 4{x^2} + 9 = 0$.
-
A.
$0$
-
B.
$1$
-
C.
$3$
-
D.
$2$
Đáp án : D
Giải phương trình bằng cách đưa về bình phương của một số.
Ta có $ - 4{x^2} + 9 = 0$
$ 4{x^2} = 9\\{x^2} = \dfrac{9}{4} $
Suy ra \(x = \dfrac{3}{2}\) hoặc \(x = - \dfrac{3}{2}\)
Phương trình có hai nghiệm $x = \dfrac{3}{2};x = - \dfrac{3}{2}$.
Xác định giá trị của tham số $m$ để hệ phương trình \(\left\{ \begin{array}{l}x + y = - 1\\mx + y = 2m\end{array} \right.\) vô nghiệm.
-
A.
$m = 1$
-
B.
$m = - 1$
-
C.
$m = 0$
-
D.
$m = \dfrac{1}{2}$
Đáp án : A
Xét hệ phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) (các hệ số khác $0$)
- Hệ phương trình có nghiệm duy nhất \( \Leftrightarrow \dfrac{a}{{a'}} \ne \dfrac{b}{{b'}}\)
- Hệ phương trình vô nghiệm \( \Leftrightarrow \dfrac{a}{{a'}} = \dfrac{b}{{b'}} \ne \dfrac{c}{{c'}}\)
- Hệ phương trình có vô số nghiệm \( \Leftrightarrow \dfrac{a}{{a'}} = \dfrac{b}{{b'}} = \dfrac{c}{{c'}}\)
Để hệ phương trình \(\left\{ \begin{array}{l}x + y = - 1\\mx + y = 2m\end{array} \right.\) vô nghiệm thì $\dfrac{m}{1} = \dfrac{1}{1} \ne \dfrac{{2m}}{1} $
\(\Leftrightarrow \left\{ \begin{array}{l}m = 1\\m \ne \dfrac{1}{2}\end{array} \right. \Rightarrow m = 1\)
Cho hệ phương trình \(\left\{ \begin{array}{l}8x + 7y = 16\\8x - 3y = - 24\end{array} \right.\) . Nghiệm của hệ phương trình là
-
A.
$\left( {x;y} \right) = \left( { - \dfrac{3}{2};4} \right)$
-
B.
$\left( {x;y} \right) = \left( {4; - \dfrac{3}{2}} \right)$
-
C.
$\left( {x;y} \right) = \left( { - \dfrac{3}{2}; - 4} \right)$
-
D.
$\left( {x;y} \right) = \left( { - 2;2} \right)$
Đáp án : A
Ta có \(\left\{ \begin{array}{l}8x + 7y = 16\\8x - 3y = - 24\end{array} \right.\)$ \Leftrightarrow \left\{ \begin{array}{l}8x + 7y = 16\\8x + 7y - \left( {8x - 3y} \right) = 16 - \left( { - 24} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8x + 7y = 16\\10y = 40\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 4\\8x + 7.4 = 16\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 4\\x = - \dfrac{3}{2}\end{array} \right.$
Vậy hệ phương trình có nghiệm duy nhất $\left( {x;y} \right) = \left( { - \dfrac{3}{2};4} \right)$
Tính $\Delta '$ và tìm số nghiệm của phương trình \(7{x^2} - 12x + 4 = 0\) .
-
A.
$\Delta ' = 6$ và phương trình có hai nghiệm phân biệt
-
B.
$\Delta ' = 8$ và phương trình có hai nghiệm phân biệt
-
C.
$\Delta ' = 8$ và phương trình có nghiệm kép
-
D.
$\Delta ' = 0$ và phương trình có hai nghiệm phân biệt
Đáp án : B
Xét phương trình bậc hai một ẩn $a{{x}^{2}}+bx+c=0\left( a\ne 0 \right)$, với $b=2b'$ và $\Delta '=b{{'}^{2}}-ac$.
- Nếu $\Delta '>0$ thì phương trình có hai nghiệm phân biệt:
${{x}_{1}}=\frac{-b'+\sqrt{\Delta '}}{a};{{x}_{2}}=\frac{-b'-\sqrt{\Delta '}}{a}$.
- Nếu $\Delta '=0$ thì phương trình có nghiệm kép ${{x}_{1}}={{x}_{2}}=-\frac{b'}{a}$.
- Nếu $\Delta '<0$ thì phương trình vô nghiệm.
Phương trình \(7{x^2} - 12x + 4 = 0\) có $a = 7;b' = - 6;c = 4$ suy ra
$\Delta ' = {\left( {b'} \right)^2} - ac = {\left( { - 6} \right)^2} - 4.7 = 8 > 0$
Nên phương trình có hai nghiệm phân biệt.
Một ô tô đi quãng đường $AB$ với vận tốc $50\,\,km/h$ , rồi đi tiếp quãng đường $BC$ với vận tốc $45km/h.$ Biết quãng đường tổng cộng dài $165\,\,km$ và thời gian ô tô đi trên quãng đường $AB$ ít hơn thời gian đi trên quãng đường $BC$ là $30$ phút. Tính thời gian ô tô đi trên đoạn đường $AB$.
-
A.
$2$ giờ
-
B.
$1,5$ giờ
-
C.
$1$ giờ
-
D.
$3$ giờ
Đáp án : B
Gọi thời gian ô tô đi trên mỗi đoạn đường $AB$ và $BC$ lần lượt là $x,y$
($x>0;y>0,5$ ; đơn vị : giờ). Ta có hệ phương trình :
\(\left\{ \begin{array}{l}50.x + 45.y = 165\\y - x = 0,5\end{array} \right. \\ \left\{ \begin{array}{l}x = 1,5\\y = 2\end{array} (TM) \right.\)
Vậy thời gian ô tô đi hết quãng đường $AB$ là $1,5$ giờ. Thời gian ô tô đi hết quãng đường $BC$ là $2$ giờ.
Cho hệ phương trình $\left\{ \begin{array}{l}x - y = 5\\3x + 2y = 18\end{array} \right.$có nghiệm $\left( {x;y} \right)$. Tích $x.y$ là
-
A.
$5$
-
B.
$\dfrac{84}{25}$
-
C.
$\dfrac{25}{84}$
-
D.
$\dfrac{84}{5}$
Đáp án : B
Từ phương trình thứ nhất, ta có: \(x = y + 5\)
Thay vào phương trình thứ hai, ta được:
\(3.\left( {y + 5} \right) + 2y = 18\\3y + 15 + 2y = 18\\5y = 3\\y = \dfrac{3}{5}\)
Thay vào \(x = y + 5\), ta được: \(x = \dfrac{3}{5}+ 5 = \dfrac{28}{5}\)
Vậy hệ phương trình có nghiệm duy nhất $\left( {x;y} \right) = \left( {\dfrac{28}{5};\dfrac{3}{5}} \right)$
Suy ra $x.y = \dfrac{28}{5}.\dfrac{3}{5} = \dfrac{84}{25}$
Cho hàm số $y = f\left( x \right) = \left( { - 2m + 1} \right){x^2}.$
Tìm giá trị của $m$ để đồ thị đi qua điểm $A\left( { - 2;4} \right).$
-
A.
$m = 0$
-
B.
$m = 1$
-
C.
$m = 2$
-
D.
$m = - 2$
Đáp án : A
Đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( {{x_0};{y_0}} \right)\) khi \({y_0} = a{x_o}^2\).
Thay tọa độ điểm $A\left( { - 2;4} \right)$ vào hàm số $y = f\left( x \right) = \left( { - 2m + 1} \right){x^2}$ ta được
$\left( { - 2m + 1} \right).{\left( { - 2} \right)^2} = 4 \\ - 2m + 1 = 1 \\ m = 0$
Vậy $m = 0$ là giá trị cần tìm.
Cho đường tròn $(O)$ đường kính $AB$ và một cung $AC$ có số đo nhỏ hơn $90^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai ?
-
A.
$AC = BE$
-
B.
Số đo cung$AD$ bằng số đo cung $BE$
-
C.
Số đo cung $AC$ bằng số đo cung $BE$
-
D.
$\widehat {AOC} < \widehat {AOD}$
Đáp án : D
Sử dụng liên hệ giữa dây và đường kính để so sánh các góc ở tâm từ đó so sánh các cung và dây cung
Vì $AO \bot CD;AO{\rm{//}}DE \Rightarrow CD \bot DE$$ \Rightarrow \widehat {CDE} = 90^\circ $ mà $C,D,E \in \left( O \right)$ nên $CE$ là đường kính hay $C;O;E$ thẳng hàng
Xét $\left( O \right)$ có $OA$ là đường cao trong tam giác cân $ODC$ nên $OA$ cũng là đường phân giác $ \Rightarrow \widehat {COA} = \widehat {AOD}$
Suy ra cung $AD$ bằng cung $AC$ nên dây $AD = AC$
Lại thấy $\widehat {AOC} = \widehat {BOE}$ (đối đỉnh) nên cung $AC$ bằng cung $BE$ suy ra dây $AC = BE$.
Phương án A, B, C đúng.
Cho đường thẳng $d$ có phương trình $(2m - 4)x + (m - 1)y = m - 5$
Tìm các giá trị của tham số m để $d$ đi qua gốc tọa độ.
-
A.
$m = 2$
-
B.
$m = 1$
-
C.
$m = 5$
-
D.
$m \ne 5$
Đáp án : C
Sử dụng nhận xét
Đường thẳng $d:{\rm{ }}ax + by = c$ đi qua điểm $M({x_0},\,{y_0})$khi và chỉ khi $a{x_0} + b{y_0} = c$.
Gốc tọa độ \(O\left( {0;0} \right)\)
Để $d$ đi qua gốc tọa độ thì tọa độ điểm \(O\) thỏa mãn phương trình $(2m - 4)x + (m - 1)y = m - 5$ hay
$(2m - 4).0 + (m - 1).0 = m - 5 \Leftrightarrow m - 5 = 0 \Leftrightarrow m = 5$
Vậy $m = 5$.
Xác định giá trị của tham số $m$ để hệ phương trình \(\left\{ \begin{array}{l}x - \left( {m - 2} \right)y = 2\\\left( {m - 1} \right)x - 2y = m - 5\end{array} \right.\) có nghiệm duy nhất
-
A.
$m \ne 0$
-
B.
$m \ne 2$
-
C.
$m \ne \left\{ {0;3} \right\}$
-
D.
$m = 0;m = 3$
Đáp án : C
Xét hệ phương trình $\left\{ \begin{array}{l}ax + by = c\,\,\,\,\,\,\,\,\,\,(1)\\a'x + b'y = c'\,\,\,(2)\end{array} \right.$ có \(d\) là đường thẳng biểu diễn tập nghiệm của phương trình \(\left( 1 \right)\) và \(d'\) là đường thẳng biểu diễn tập nghiệm của phương trình \(\left( 2 \right)\), khi đó \(d \cap d' = A\left( {{x_0};{y_0}} \right) \Leftrightarrow \) Hệ phương trình có nghiệm duy nhất.
Xét hệ \(\left\{ \begin{array}{l}x - \left( {m - 2} \right)y = 2\\\left( {m - 1} \right)x - 2y = m - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {m - 2} \right)y = x - 2\\2y = \left( {m - 1} \right)x - m + 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {m - 2} \right)y = x - 2\\y = \dfrac{{m - 1}}{2}x - \dfrac{m}{2} + \dfrac{5}{2}\end{array} \right.\)
TH1: Với \(m - 2 = 0 \Leftrightarrow m = 2\) ta có hệ \(\left\{ \begin{array}{l}0.y = x - 2\\y = \dfrac{1}{2}x + \dfrac{3}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = \dfrac{1}{2}x + \dfrac{3}{2}\end{array} \right.\)
Nhận thấy hệ này có nghiệm duy nhất vì hai đường thẳng \(x = 2\) và \(y = \dfrac{1}{2}x + \dfrac{3}{2}\) cắt nhau.
TH2: Với \(m - 2 \ne 0 \Leftrightarrow m \ne 2\) ta có hệ \(\left\{ \begin{array}{l}\left( {m - 2} \right)y = x - 2\\y = \dfrac{{m - 1}}{2}x - \dfrac{m}{2} + \dfrac{5}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{1}{{m - 2}}x - \dfrac{2}{{m - 2}}\\y = \dfrac{{m - 1}}{2}x - \dfrac{m}{2} + \dfrac{5}{2}\end{array} \right.\)
Để hệ phương trình đã cho có nghiệm duy nhất thì hai đường thẳng \(d:y = \dfrac{1}{{m - 2}}x - \dfrac{2}{{m - 2}}\) và \(d':y = \dfrac{{m - 1}}{2}x - \dfrac{m}{2} + \dfrac{5}{2}\) cắt nhau
\( \Leftrightarrow \dfrac{1}{{m - 2}} \ne \dfrac{{m - 1}}{2} \Leftrightarrow \left( {m - 1} \right)\left( {m - 2} \right) \ne 2 \Leftrightarrow {m^2} - 3m + 2 \ne 2 \Leftrightarrow {m^2} - 3m \ne 0\)
\( \Leftrightarrow m\left( {m - 3} \right) \ne 0 \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne 3\end{array} \right.\)
Suy ra $m \ne \left\{ {0;2;3} \right\}$
Kết hợp cả TH1 và TH2 ta có $ m\ne \left\{ {0;3} \right\}.$
Vậy hệ phương trình đã cho có nghiệm duy nhất khi \(m \ne \left\{ {0;3} \right\}\)
Kết luận nào đúng khi nói về nghiệm $\left( {x;y} \right)$ của hệ phương trình \(\left\{ \begin{array}{l}x + \dfrac{y}{2} = \dfrac{{2x - 3}}{2}\\\dfrac{x}{2} + 3y = \dfrac{{25 - 9y}}{8}\end{array} \right.\)
-
A.
$x > 0;y < 0$
-
B.
$x < 0;y < 0$
-
C.
$x < 0;y > 0$
-
D.
$x > 0;y > 0$
Đáp án : A
Giải hệ phương trình quy về hệ phương trình bậc nhất hai ẩn sau đó sử dụng phương pháp cộng đại số.
Ta có
\(\left\{ \begin{array}{l}x + \dfrac{y}{2} = \dfrac{{2x - 3}}{2}\\\dfrac{x}{2} + 3y = \dfrac{{25 - 9y}}{8}\end{array} \right.\)
$\left\{ \begin{array}{l}2x + y = 2x - 3\\4x + 24y = 25 - 9y\end{array} \right. $
$\left\{ \begin{array}{l}y = - 3\\4x + 33y = 25\end{array} \right.$
$\left\{ \begin{array}{l}x = 31\\y = - 3\end{array} \right.$
Vậy hệ phương trình có nghiệm duy nhất $\left( {x;y} \right) = \left( {31; - 3} \right)$ .
$ \Rightarrow x > 0;y < 0$
Cho hệ phương trình $\left\{ \begin{array}{l}x + 2y = m + 3\\2x - 3y = m\end{array} \right.$ ( $m$ là tham số) . Tìm $m$ để hệ có nghiệm duy nhất $\left( {x,y} \right)$ thỏa mãn $x + y = - 3$.
-
A.
$m = - 6$
-
B.
$m = 6$
-
C.
$m = 3$
-
D.
$m = - 4$
Đáp án : A
Bước 1: Giải hệ phương trình tìm được nghiệm $\left( {x,y} \right)$ theo tham số $m$
Bước 2: Thay $x,y$ vừa tìm được vào hệ thức yêu cầu để tìm $m$
Ta có $\left\{ \begin{array}{l}x + 2y = m + 3\\2x - 3y = m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 4y = 2m + 6\\2x - 3y = m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + 2y = m + 3\\7y = m + 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{5m + 9}}{7}\\y = \dfrac{{m + 6}}{7}\end{array} \right.$
Hệ phương trình có nghiệm duy nhất $\left( {x;y} \right) = \left( {\dfrac{{5m + 9}}{7};\dfrac{{m + 6}}{7}} \right)$.
Lại có $x + y = - 3$ hay $\dfrac{{5m + 9}}{7} + \dfrac{{m + 6}}{7} = - 3 \Leftrightarrow 5m + 9 + m + 6 = - 21 \Leftrightarrow 6m = - 36 \Leftrightarrow m = - 6$
Vậy với $m = - 6$ thì hệ phương trình có nghiệm duy nhất $\left( {x,y} \right)$ thỏa mãn $x + y = - 3$.
Hai trường có tất cả 300 học sinh tham gia một cuộc thi. Biết trường A có $75\% $ học sinh đạt, trường 2 có $60\% $ đạt nên cả 2 trường có 207 học sinh đạt. Số học sinh dự thi của trường A và trường B lần lượt là:
-
A.
160 và 140
-
B.
200 và 100
-
C.
180 và 120
-
D.
Tất cả đều sai
Đáp án : C
Gọi số học sinh của trường thứ nhất dự thi là x (học sinh) $(x \in N^*,x < 300)$;
số học sinh của trường thứ 2 dự thi là y (học sinh) $(y \in N^*;\,\,y < 300)$.
Lập hệ phương trình và giải hệ đó.
Gọi số học sinh của trường thứ nhất dự thi là x (học sinh) $(x \in N^*,x < 300)$;
số học sinh của trường thứ 2 dự thi là y (học sinh) $(y \in N^*;\,\,y < 300)$.
Hai trường có tất cả 300 học sinh tham gia cuộc thi nên ta có phương trình: $x + y = 300\begin{array}{*{20}{c}}{}&{(1)}\end{array}$
Trường A có 75% học sinh đạt, trường 2 có 60% đạt nên cả 2 trường có 207 học sinh đạt, ta có: $\dfrac{{75}}{{100}}x + \dfrac{{60}}{{100}}y = 207\begin{array}{*{20}{c}}{}&{(2)}\end{array}$
Từ (1) và (2) ta có hệ phương trình:
$\left\{ \begin{array}{l}x + y = 300\\\dfrac{{75}}{{100}}x + \dfrac{{60}}{{100}}y = 207\end{array} \right. $
Nhân hai vế của phương trình thứ nhất với $\dfrac{{60}}{{100}}$, ta được $\left\{ \begin{array}{l}\dfrac{{60}}{{100}}x + \dfrac{{60}}{{100}}y = 180\\\dfrac{{75}}{{100}}x + \dfrac{{60}}{{100}}y = 207\end{array} \right.$
Trừ cả hai vế của phương trình thứ hai cho phương trình thứ nhất, ta được: $\dfrac{{15}}{{100}}x = 27$ suy ra $x = 180$
Thay vào \(x + y = 300\) suy ra $y = 120 (tm)$
Vậy số học sinh của trường thứ nhất dự thi là 180 học sinh; số học sinh của trường thứ 2 dự thi là 120 học sinh.
Cho hàm số \(y = - \dfrac{2}{5}{x^2}\,\,\)có đồ thị là \((P)\). Điểm trên \(\left( P \right)\) (khác gốc tọa độ \(O\left( {0;0} \right)\)) có tung độ gấp ba lần hoành độ thì có hoành độ là:
-
A.
\(\dfrac{{15}}{2}\)
-
B.
\(\dfrac{{ - 15}}{2}\)
-
C.
\(\dfrac{2}{{15}}\)
-
D.
\( - \dfrac{2}{{15}}\)
Đáp án : B
Bước 1: Gọi điểm \(M\)\(\left( {x;y} \right)\) thỏa mãn điều kiện đề bài. Biểu diễn \(x\) theo \(y\) hoặc \(y\) theo \(x\) .
Bước 2: Thay tọa độ điểm \(M\) vào hàm số ta tìm được \(x\) từ đó suy ra \(M\).
Gọi điểm \(M\)\(\left( {x;y} \right)\) là điểm cần tìm. Vì \(M\) có tung độ gấp ba lần hoành độ nên \(M\left( {x;3x} \right)\).
Thay tọa độ điểm \(M\) vào hàm số ta được
\(3x = - \dfrac{2}{5}{x^2} \\ \dfrac{2}{5}{x^2} + 3x = 0 \\ x\left( {\dfrac{2}{5}x + 3} \right) = 0\)
Suy ra \(x = 0 \) hoặc \({\dfrac{2}{5}x + 3} = 0\)
\(x = 0 \) hoặc \( x = - \dfrac{{15}}{2}\)
+ Với \(x = 0 \) ta được \( y = 0\). Suy ra điểm \(O\left( {0;0} \right)\).
+ Với \( x = - \dfrac{{15}}{2}\) ta được \(y = \dfrac{{ - 45}}{2}\). Suy ra điểm \(M\left( {\dfrac{{ - 15}}{2};\dfrac{{ - 45}}{2}} \right)\).
Vậy điểm khác gốc tọa độ thỏa mãn điều kiện là \(M\left( {\dfrac{{ - 15}}{2};\dfrac{{ - 45}}{2}} \right)\).
Tìm điều kiện của tham số m để phương trình \(2{x^2} + 5x + m - 1 = 0\) vô nghiệm
-
A.
\(m > \dfrac{8}{{33}}\)
-
B.
Không tồn tại \(m\)
-
C.
\(m < \dfrac{{33}}{8}\)
-
D.
\(m > \dfrac{{33}}{8}\)
Đáp án : D
Xét phương trình bậc hai: ${\rm{a}}{{\rm{x}}^2} + bx + c = 0\,\,(a \ne 0)$
Bước 1: Kiểm tra điều kiện của phương trình bậc hai một ẩn: $a \ne 0$
Bước 2: Tính biệt thức \(\Delta\), với \(\Delta < 0\) thì phương trình vô nghiệm.
Phương trình \(2{x^2} + 5x + m - 1 = 0\) có $a = 2$ nên là phương trình bậc hai ẩn x.
Biệt thức $ \Delta = {5^2} - 4.2\left( {m - 1} \right) = 25 - 8m + 8 = 33 - 8m\,$
Phương trình đã cho vô nghiệm khi $\Delta < 0$ hay $33 - 8m < 0$ suy ra $m > \dfrac{{33}}{8}$
Vậy với \(m > \dfrac{{33}}{8}\) thì phương trình vô nghiệm.
Cho phương trình \((m - 2){x^2} - 2(m + 1)x + m = 0\). Tìm các giá trị của $m$ để phương trình có một nghiệm
-
A.
$m = - 2$
-
B.
$m = 2;m = - \dfrac{1}{4}$
-
C.
$m = - \dfrac{1}{4}$
-
D.
$m \ne 2$
Đáp án : B
Xét phương trình bậc hai dạng $a{x^2} + bx + c = 0$ với $b = 2b'$
TH1: $a = 0$
TH2: $a \ne 0$. Khi đó, p hương trình có nghiệm kép\( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta ' = 0\end{array} \right.\)
Phương trình \((m - 2){x^2} - 2(m + 1)x + m = 0\) có $a = m - 2;b' = - \left( {m + 1} \right);c = m$
Suy ra $\Delta ' = {\left( {m + 1} \right)^2} - \left( {m - 2} \right)m = 4m + 1$
TH1: $m - 2 = 0 \Leftrightarrow m = 2 \Rightarrow - 6x + 2 = 0 \Leftrightarrow x = \dfrac{1}{3}$. Với $m = 2$ phương trình có một nghiệm $x = \dfrac{1}{3}$
TH2: $m - 2 \ne 0 \Leftrightarrow m \ne 2$
Để phương trình có nghiệm kép thì $\left\{ \begin{array}{l}a \ne 0\\\Delta ' = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 2\\4m + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 2\\m = - \dfrac{1}{4}\end{array} \right. \Rightarrow m = - \dfrac{1}{4}$
Vậy $m = - \dfrac{1}{4}$ và $m = 2$ là giá trị cần tìm.
Cho đường tròn $(O).$ Từ một điểm $M$ ở ngoài $(O)$, vẽ hai tiếp tuyến $MA$ và $MB$ sao cho góc $AMB$ bằng ${120^0}$. Biết chu vi tam giác $MAB$ là $6\left( {3 + 2\sqrt 3 } \right)cm$, tính độ dài dây $AB.$
-
A.
$18\,cm$
-
B.
$6\sqrt 3 cm$
-
C.
$12\sqrt 3 \,cm$
-
D.
$15\,cm$
Đáp án : A
Sử dụng tính chất hai tiếp tuyến cắt nhau và công thức chu vi tam giác
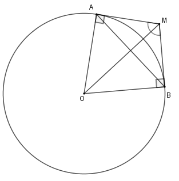
Xét $\left( O \right)$ có $MA = MB$; $\widehat {AMO} = \widehat {BMO}$ (tính chất hai tiếp tuyến cắt nhau)
Nên $\widehat {AMO} = 60^\circ $. Xét tam giác vuông $AOM$ có $AM = AO.cot\widehat {AMO} = \dfrac{{R\sqrt 3 }}{3}$ nên $MA = MB = \dfrac{{R\sqrt 3 }}{3}$
Lại có $\widehat {AOB} + \widehat {AMB} = 180^\circ \Rightarrow \widehat {AOB} = 60^\circ $ suy ra $\Delta AOB$ là tam giác đều $ \Rightarrow AB = OB = OA = R$
Chu vi tam giác $MAB$ là $MA + MB + AB = \dfrac{{R\sqrt 3 }}{3} + \dfrac{{R\sqrt 3 }}{3} + R = 6\left( {3 + 2\sqrt 3 } \right)$
hay $ R\left( {\dfrac{{3 + 2\sqrt 3 }}{3}} \right) = 6\left( {3 + 2\sqrt 3 } \right) \Rightarrow R = 18\,cm$ nên $AB = 18\,cm$.
Cho hai đường tròn $\left( {O;20cm} \right)$ và $\left( {O';15cm} \right)$ cắt nhau tại $A$ và$B$. Tính đoạn nối tâm $OO'$, biết rằng$AB = 24cm$ và $O$ và $O'$ nằm cùng phía đối với $AB$ .
-
A.
$OO' = 7cm$
-
B.
$OO' = 8cm$
-
C.
$OO' = 9cm$
-
D.
$OO' = 25cm$
Đáp án : A
Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và định lý Pytago
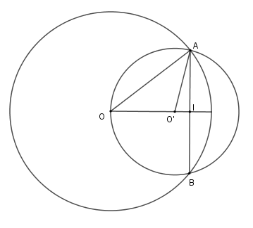
Ta có: $AI = \dfrac{1}{2}AB = 12\,\ cm$
Theo định lý Pytago ta có
$O{I^2} = O{A^2}-A{I^2} = 256$ $ \Rightarrow $ $OI = 16 \,\ cm$ và $O'I = \sqrt {O'{A^2} - I{A^2}} = 9 \,\ cm$
Do đó: $OO' = OI-O'I = 16-9 = 7\left( {cm} \right)$ .
Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\)tiếp xúc ngoài tại \(A\). Kẻ các đường kính \(AOB;AO'C\). Gọi \(DE\) là tiếp tuyến chung của hai đường tròn \(\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)\). Gọi \(M\) là giao điểm của \(BD\) và \(CE\). Tính diện tích tứ giác \(ADME\) biết \(\widehat {DOA} = 60^\circ \) và \(OA = 8\,cm\)
-
A.
\(12\sqrt 3 \,\,c{m^2}\)
-
B.
\( \dfrac{64}{3}\sqrt 3 \,\,c{m^2}\)
-
C.
\( \dfrac{32}{3}\sqrt 3 \,\,c{m^2}\)
-
D.
\(36\,\,c{m^2}\)
Đáp án : B
Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và hệ thức lượng trong tam giác vuông.
Diện tích hình chữ nhật bằng tích chiều dài và chiều rộng.
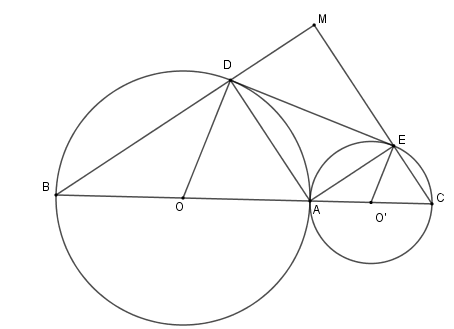
Xét \(\left( O \right)\) có \(OD = OA \Rightarrow \Delta OAD\) cân tại \(O \Rightarrow \widehat {ODA} = \widehat {OAD}\)
Xét \(\left( {O'} \right)\) có \(O'E = O'A \Rightarrow \Delta O'EB\) cân tại \(O' \Rightarrow \widehat {O'EA} = \widehat {O'AE}\)
Mà \(\widehat O + \widehat {O'} = 360^\circ - \widehat {O'ED} - \widehat {ODE} = 180^\circ \)
\( \Leftrightarrow 180^\circ - \widehat {ODA} - \widehat {OAD} + 180^\circ - \widehat {O'EA} - \widehat {O'AE} = 180^\circ \Leftrightarrow 2\left( {\widehat {OAD} + \widehat {O'AE}} \right) = 180^\circ \)
\( \Rightarrow \widehat {OAD} + \widehat {O'AE} = 90^\circ \)\( \Rightarrow \widehat {DAE} = 90^\circ \Rightarrow \Delta ADE\) vuông tại \(A\).
Mà \(\widehat {BDA} = 90^\circ \) ( vì tam giác \(BAD\) có cạnh \(AB\) là đường kính của \(\left( O \right)\)và \(D \in \left( O \right)\) ) nên \(BD \bot AD \Rightarrow \widehat {MDA} = 90^\circ \)
Tương tự ta có \(\widehat {MEA} = 90^\circ \) .\(\)\(\)
Nên tứ giác \(DMEA\) là hình chữ nhật.
Xét tam giác \(OAD\) cân tại \(O\) có \(\widehat {DOA} = 60^\circ \) nên \(\Delta DOA\) đều, suy ra \(OA = AD = 8\,cm\) và \(\widehat {ODA} = 60^\circ \)
\( \Rightarrow \widehat {ADE} = 30^\circ \). Xét tam giác \(ADE\) ta có \(EA = AD.\tan \widehat {EDA} = 8.\tan 30^\circ = \dfrac{8}{3}\sqrt 3 \)
\({S_{DMEA}} = AD.AE = 8.\dfrac{8}{3}\sqrt 3 = \dfrac{64}{3}\sqrt 3 \,\,c{m^2}\).
Cho đường tròn \(\left( O \right)\) đường kính \(AB,\) vẽ góc ở tâm \(\widehat {AOC} = 60^\circ \) . Vẽ dây \(CD\) vuông góc với \(AB\) và dây \(DE\) song song với \(AB.\) Tính số đo cung nhỏ \(BE\)
-
A.
$120^\circ $
-
B.
$60^\circ $
-
C.
$240^\circ $
-
D.
$30^\circ $
Đáp án : B
Bước 1: Chứng minh $E;O;C$ thẳng hàng
Bước 2: Tính số đo cung thông qua góc ở tâm
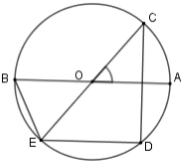
Xét $\left( O \right)$ có $CD \bot OA;ED{\rm{//}}OA \Rightarrow CD \bot ED$ hay $\widehat {EDC} = 90^\circ $ mà $E;D;C \in \left( O \right)$ nên $EC$ là đường kính của $\left( O \right)$ hay $E;O;C$ thẳng hàng.
Do đó $\widehat {BOE} = \widehat {COA} = 60^\circ $ (đối đỉnh) nên số đo cung nhỏ $BE$ là $60^\circ $.
Cho tam giác $ABC$ cân tại $A$ và $\widehat A = 66^\circ $ nội tiếp đường tròn $\left( O \right)$. Trong các cung nhỏ $AB;BC;AC$, cung nào là cung lớn nhất?
-
A.
$AB$
-
B.
$AC$
-
C.
$BC$
-
D.
$AB,AC$
Đáp án : C
Sử dụng mối liên hệ giữa cung và dây
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
+) Cung lớn hơn căng dây lớn hơn.
+) Dây lớn hơn căng cung lớn hơn.
+) Hai cung bằng nhau căng hai dây bằng nhau và ngược lại
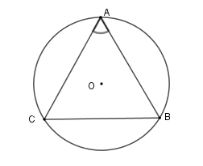
Vì tam giác $ABC$ cân tại $A$ có $\widehat A = 66^\circ \Rightarrow \widehat B = \widehat C = \dfrac{{180^\circ - \widehat A}}{2} = \dfrac{{180^\circ - 66^\circ }}{2} = 57^\circ $
Vì $\widehat A > \widehat B = \widehat C$ nên theo mối liên hệ giữa cạnh và góc trong tam giác ta có $BC > AB = AC$
Theo mối liên hệ giữa cung và dây ta có $\overparen{BC}$ $ > $ $\overparen{AB}$ $ = $ $\overparen{AC}$.
Cho đường tròn $\left( {O;R} \right)$ và hai dây $AB;CD$ sao cho $\widehat {AOB} = 120^\circ ;\widehat {COD} = 60^\circ $. So sánh các dây $CD;AB$.
-
A.
$CD = 2AB$
-
B.
$AB > 2CD$
-
C.
$CD > AB$
-
D.
$CD < AB < 2CD$
Đáp án : D
Sử dụng mối liên hệ giữa cung và dây
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
+) Cung lớn hơn căng dây lớn hơn.
+) Dây lớn hơn căng cung lớn hơn.
+) Hai cung bằng nhau căng hai dây bằng nhau và ngược lại
Sử dụng định lý: Trong một đường tròn, đường kính là dây có độ dài lớn nhất
Vì $\widehat {COD} < \widehat {AOB}$ nên cung $CD$ nhỏ hơn cung $AB$, từ đó dây $CD < AB$ (*)
Xét tam giác $OCD$ cân tại $O$ có $\widehat {COD} = 60^\circ $ nên $\Delta COD$ là tam giác đều $ \Rightarrow CD = R$
$AB$ là dây không đi qua tâm nên $AB < 2R \Rightarrow AB < 2CD$ (**)
Từ (*) và (**) ta có $CD < AB < 2CD$
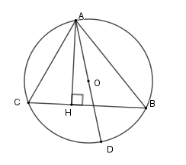
Cho tam giác $ABC$ có \(AB = 5cm;AC = 3cm\) thuộc đường tròn tâm $(O),$ đường cao $AH$, đường kính $AD.$ Khi đó tích $AH.AD$ bằng
-
A.
\(15c{m^2}\)
-
B.
$8c{m^2}$
-
C.
\(12c{m^2}\)
-
D.
$30c{m^2}$
Đáp án : A
Sử dụng tính chất góc nội tiếp để chứng minh các góc bằng nhau để chứng minh hai tam giác đồng dạng.
Xét \(\left( O \right)\) có \(\widehat {ACB} = \widehat {ADB}\) (hai góc nội tiếp cùng chắn cung \(AB\) ); \(\widehat {ABD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Nên \(\Delta ACH \backsim \Delta ADB\left( {g - g} \right)\)
Suy ra $\dfrac{{AC}}{{AD}} = \dfrac{{AH}}{{AB}}$
Do đó $AH.AD = AC.AB$.
Suy ra \(AH.AD = 3.5 = 15c{m^2}\) .
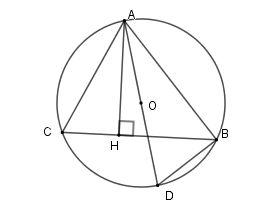
Cho tam giác ABC nằm trên đường tròn $(O;R), $đường cao $AH,$ biết $AB = 9{\rm{ }}cm,$ $AC = 12{\rm{ }}cm,$ $AH = 4{\rm{ }}cm.$ Tính bán kính của đường tròn $(O)$.
-
A.
\(13,5\,cm\)
-
B.
$12\,cm$
-
C.
\(18\,cm\)
-
D.
$6\,cm$
Đáp án : A
Kẻ đường kính \(AD\)
Chứng minh \(\Delta ACH \backsim \Delta ADB\left( {g - g} \right)\)
Suy ra \( AD = \dfrac{{AB.AC}}{{AH}}\)
Kẻ đường kính \(AD\)
Xét \(\left( O \right)\) có \(\widehat {ACB} = \widehat {ADB}\) (hai góc nội tiếp cùng chắn cung \(AB\) ); \(\widehat {ABD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Nên \(\Delta ACH \backsim \Delta ADB\left( {g - g} \right)\)
Suy ra $\dfrac{{AC}}{{AD}} = \dfrac{{AH}}{{AB}}$
Do đó $AH.AD = AC.AB$
Suy ra \(AD = \dfrac{{AB.AC}}{{AH}} = \dfrac{{9.12}}{4} = 27\)
Do đó \(R = 13,5cm\) .
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) có \(AC = 3cm\) . Kẻ tiếp tuyến \(xAy\) với \(\left( O \right)\) . Từ \(C\) kẻ \(CM{\rm{//}}xy\left( {M \in AB} \right)\) . Chọn câu đúng.
-
A.
\(AM.AB = 12c{m^2}\)
-
B.
\(AM.AB = 6c{m^2}\)
-
C.
\(AM.AB = 9c{m^2}\)
-
D.
\(AM.AB = B{C^2}\)
Đáp án : C
Sử dụng hệ quả về góc tạo bởi tiếp tuyến và dây cung: “ Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau” để chứng minh các góc bằng nhau
Từ đó suy ra tam giác đồng dạng theo trường hợp góc-góc và suy ra hệ thức tương ứng.
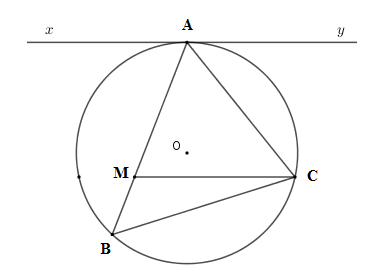
Ta có \(\widehat {yAC} = \widehat {ABC}\) (hệ quả góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC\) ) mà \(\widehat {yAC} = \widehat {ACM}\) (so le trong) nên \(\widehat {ABC} = \widehat {ACM} \Rightarrow \Delta AMC\backsim\Delta ACB\left( {g - g} \right)\)
\(\dfrac{{AM}}{{AC}} = \dfrac{{AC}}{{AB}} \Rightarrow AM.AB = A{C^2} = {3^2} = 9\left( {c{m^2}} \right)\) .
Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$ cắt nhau tại $A$ và $B$. Một đường thẳng tiếp xúc với $\left( O \right)$ tại $C$, và tiếp xúc với đường tròn $\left( {O'} \right)$ tại $D$ sao cho tia \(AB\) cắt đoạn \(CD\). Vẽ đường tròn $\left( I \right)$ đi qua ba điểm $A,C,D$ cắt đường thẳng $AB$ tại một điểm thứ hai là $E$. Chọn câu đúng:
-
A.
Tứ giác $BCED$ là hình thoi
-
B.
Tứ giác $BCED$ là hình bình hành
-
C.
Tứ giác $BCED$ là hình vuông
-
D.
Tứ giác $BCED$ là hình chữ nhật
Đáp án : B
Sử dụng các tính chất: góc nội tiếp cùng chắn một cung; góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung.
Sử dụng dấu hiệu nhận biết một hình là hình bình hành, hình thoi, hình chữ nhật, hình vuông.
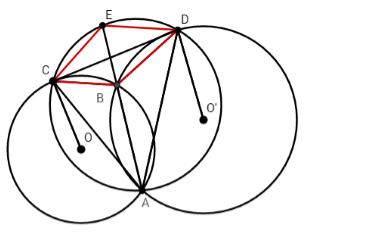
+) Xét $\left( O \right)$ ta có:
\(\widehat {BAC} = \widehat {BCD}\) (cùng chắn cung $CB$)
Xét $\left( I \right)$ có:
\(\widehat {CAB} = \widehat {EDC}\) (cùng chắn cung \(CE\))
\( \Rightarrow \widehat {BCD} = \widehat {EDC} \Rightarrow ED//BC\left( 1 \right)\)
+) Xét $\left( {O'} \right)$ có:
\(\widehat {BAD} = \widehat {BDC}\) (cùng chắn cung $BD$)
Xét $\left( I \right)$ có:
\(\widehat {EAD} = \widehat {ECD}\) (cùng chắn cung $ED$)
\( \Rightarrow \widehat {ECD} = \widehat {BDC} \Rightarrow CE//BD\left( 2 \right)\)
Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra $BDEC$ là hình bình hành
Tìm \(m\) để hai phương trình \({x^2} + mx + 2 = 0\) và \({x^2} + 2x + m = 0\) có ít nhất một nghiệm chung.
-
A.
\(1\)
-
B.
\( - 3\)
-
C.
\( - 1\)
-
D.
\(3\)
Đáp án : B
Hai phương trình có nghiệm chung thì nghiệm chung đó phải thoả mãn cả hai phương trình
Gọi \({x_0}\) là nghiệm chung của hai phương trình thì \({x_0}\) phải thỏa mãn hai phương trình trên.
Thay \(x = {x_0}\) vào hai phương trình trên ta được \(\left\{ \begin{array}{l}{x_0}^2 + m{x_0} + 2 = 0\\{x_0}^2 + 2{x_0} + m = 0\end{array} \right. \) \(\Rightarrow (m - 2){x_0} + 2 - m = 0\) \(\Leftrightarrow (m - 2)(x_0-1)= 0\)
+) Nếu \(m = 2\) thì \(0 = 0\) (luôn đúng) hay hai phương trình trùng nhau.
Lúc này phương trình \({x^2} + 2x + 2 = 0 \Leftrightarrow {\left( {x + 1} \right)^2} = - 1\) vô nghiệm nên cả hai phương trình đều vô nghiệm.
Vậy \(m = 2\) không thỏa mãn.
+) Nếu \(m \ne 2\) thì \({x_0} = 1\).
Thay \({x_0} = 1\) vào phương trình \({x_0}^2 + m{x_0} + 2 = 0\) ta được \(1 + m + 2 = 0 \Leftrightarrow m = - 3\).
Vậy \(m = - 3\) thì hai phương trình có nghiệm chung.
Cho đường thẳng xy và đường tròn (O; R) không giao nhau. Gọi M là một điểm di động trên xy. Vẽ đường tròn đường kính OM cắt đường tròn (O) tại A và B. Kẻ \(OH \bot xy\) . Chọn câu đúng.
-
A.
Đường thẳng AB luôn đi qua một điểm cố định là \(H.\)
-
B.
Đường thẳng AB luôn đi qua một điểm cố định là trung điểm \(OH\) .
-
C.
Đường thẳng AB luôn đi qua một điểm cố định là giao của \(OH\) và \(AB.\)
-
D.
Đường thẳng AB luôn đi qua một điểm cố định là giao của \(OH\) và \(\left( {O;R} \right).\)
Đáp án : C
+ Sử dụng tam giác đồng dạng
+ Sử dụng hệ thức lượng trong tam giác vuông để chỉ ra các điểm và đoạn thẳng cố định.
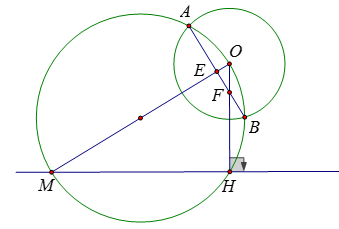
Vì \(OH \bot xy,\) nên \(H\) là một điểm cố định và \(OH\) không đổi
Gọi giao điểm của \(AB\) và \(OM\) là \(E;\) giao điểm của \(AB\) với \(OH\) là \(F.\)
Vì \(\left( {O;R} \right)\) và đường tròn đường kính \(OM\) cắt nhau tại \(A;B\) nên \(AB \bot OM\)
Lại có điểm A nằm trên đường tròn đường kính OM nên \(\widehat {OAM} = 90^\circ \)
Xét \(\Delta OEF\) và \(\Delta OHM\) có \(\widehat O\) chung và \(\widehat {OEF} = \widehat {OHM} = 90^\circ \) nên \(\Delta OEF \backsim \Delta OHM\left( {g - g} \right)\)
Suy ra \(\dfrac{{OE}}{{OH}} = \dfrac{{OF}}{{OM}} \Rightarrow OE.OM = OF.OH\)
Xét \(\Delta MAO\) vuông tại \(A\) có \(AE\) là đường cao nên theo hệ thức lượng trong tam giác vuông ta có
\(\begin{array}{*{20}{l}}{OM.OE = O{A^2}\; = {R^2}}\\{\; \Rightarrow OF.OH = {R^2}\; \Rightarrow OF = \dfrac{{{R^2}}}{{OH}}}\end{array}\)
Do \(OH\) không đổi nên \(OF\) cũng không đổi
Vậy \(F\) là một điểm cố định hay \(AB\) luôn đi qua một điểm cố định là giao của \(AB\) và \(OH.\)