Đề kiểm tra giữa học kì 1 Toán 9 - Đề số 2
Đề bài
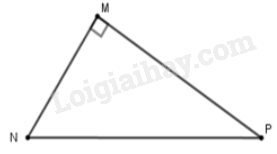
Cho tam giác $MNP$ vuông tại $M$. Khi đó $\cos \widehat {MNP}$ bằng
-
A.
$\dfrac{{MN}}{{NP}}$
-
B.
$\dfrac{{MP}}{{NP}}$
-
C.
$\dfrac{{MN}}{{MP}}$
-
D.
$\dfrac{{MP}}{{MN}}$
Một cột đèn có bóng trên mặt đất dài $7,5m.$ Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng ${42^0}.$ Tính chiều cao của cột đèn. (làm tròn đến chữ số thập phân thứ ba)
-
A.
$6,753\,m$
-
B.
$6,75\,m$
-
C.
$6,751\,m$
-
D.
$6,755\,m$
Chọn câu đúng nhất. Nếu \(\alpha \) là một góc nhọn bất kỳ, ta có
-
A.
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
-
B.
\(\tan \alpha .\cot \alpha = 1\)
-
C.
\(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}\)
-
D.
Cả A, B, C đều đúng
Cho \(B = \dfrac{2}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 3 - \sqrt 2 }} - \dfrac{2}{{\sqrt 3 - 1}}\) và \(C = \left( {2\sqrt 3 - 5\sqrt {27} + 4\sqrt {12} } \right):\sqrt 3 \). Chọn đáp án đúng.
-
A.
\(B > C\)
-
B.
\(B < C\)
-
C.
\(B = C\)
-
D.
\(B = - C\)
Cho các biểu thức $A,B$ mà $A.B \ge 0;B > 0$, khẳng định nào sau đây là đúng?
-
A.
$\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt {AB} }}{B}$
-
B.
$\sqrt {\dfrac{A}{B}}=- \dfrac{{\sqrt {AB} }}{B}$
-
C.
$\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt A }}{B}$
-
D.
$\sqrt {\dfrac{A}{B}} = \dfrac{{AB}}{{\sqrt B }}$
Cho tam giác $ABC$ vuông tại $A$ có $AB = 21\,cm$; $\widehat C = 40^\circ $ , phân giác \(BD\) (\(D\) thuộc \(AC\) ). Độ dài phân giác $BD$ là (Kết quả làm tròn đến chữ số thập phân thứ nhất)
-
A.
\(21,3\,cm\)
-
B.
\(24\,cm\)
-
C.
\(22,3\,cm\)
-
D.
\(23,2\,cm\)
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.
-
A.
$\sin \alpha + \cos \alpha = 1$
-
B.
${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
-
C.
${\sin ^3}\alpha + {\cos ^3}\alpha = 1$
-
D.
$\sin \alpha - cos\alpha = 1$
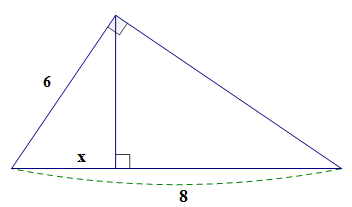
Cho hình vẽ, tìm \(x.\)
-
A.
\(x = 0,75\)
-
B.
\(x = 4,5\)
-
C.
\(x = 4\sqrt 3 \)
-
D.
\(x = 4\)
Khẳng định nào sau đây là đúng ?
-
A.
\(\sqrt {2018 + 2019} = \sqrt {2018} + \sqrt {2019} \)
-
B.
\(\sqrt {2018. 2019} = \dfrac{{\sqrt {2018} }}{{\sqrt {2019} }}\)
-
C.
\(\sqrt {2018} .\sqrt {2019} = \sqrt {2018.2019} \)
-
D.
\(2018. 2019 = \dfrac{{\sqrt {2019} }}{{\sqrt {2018} }}\)
Giá trị của biểu thức \(\sqrt {32} + \sqrt {50} - 3\sqrt 8 - \sqrt {18} \) là
-
A.
$1$
-
B.
$0$
-
C.
$2$
-
D.
$3$
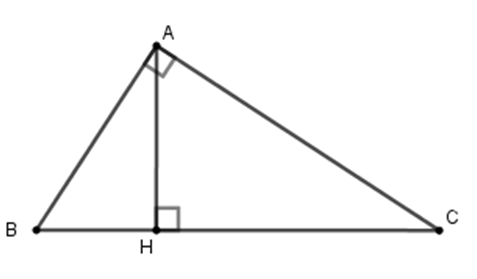
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là đúng ?
-
A.
$A{H^2} = AB.AC$
-
B.
$A{H^2} = BH.CH$
-
C.
$A{H^2} = AB.BH$
-
D.
$A{H^2} = CH.BC$
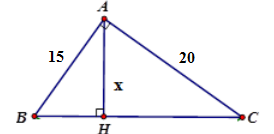
Tính \(x\) trong hình vẽ sau:
-
A.
\(x = 14\)
-
B.
\(x = 13\)
-
C.
\(x = 12\)
-
D.
\(x = \sqrt {145} \)
Tìm các số $x$ không âm thỏa mãn $\sqrt x \ge 3$
-
A.
$x \ge 9$
-
B.
$x < 9$
-
C.
$x > 9$
-
D.
$x \le 9$
So sánh hai số \(5\) và \(\sqrt {50} - 2\).
-
A.
\(5 > \sqrt {50} - 2\)
-
B.
\(5 = \sqrt {50} - 2\)
-
C.
\(5 < \sqrt {50} - 2\)
-
D.
Chưa đủ điều kiện để so sánh.
So sánh hai số \(9\sqrt 7 \) và \(8\sqrt 8 \)
-
A.
\(8\sqrt 8 < 9\sqrt 7 \)
-
B.
\(8\sqrt 8 = 9\sqrt 7 \)
-
C.
\(8\sqrt 8 \ge 9\sqrt 7 \)
-
D.
\(9\sqrt 7 < 8\sqrt 8 \)
Tìm điều kiện của $x$ để căn thức \(\sqrt {\dfrac{1}{{x - 1}}} \) có nghĩa.
-
A.
$x \ge 1$
-
B.
\(x < 1\)
-
C.
\(x > 1\)
-
D.
\(x = 1\)
Rút gọn biểu thức
$\sqrt {{a^2} + 8a + 16} + \sqrt {{a^2} - 8a + 16} $ với $ - 4 \le a \le 4$ ta được
-
A.
$2a$
-
B.
$8$
-
C.
$ - 8$
-
D.
$ - 2a$
Giá trị của biểu thức \(\sqrt {252} - \sqrt {700} + \sqrt {1008} - \sqrt {448} \) là:
-
A.
\(\sqrt 7 \)
-
B.
\(0\)
-
C.
\(4\sqrt 7 \)
-
D.
\(5\sqrt 7 \)
Rút gọn biểu thức \(5\sqrt a - 4b\sqrt {25{a^3}} + 5a\sqrt {16a{b^2}} - \sqrt {9a} \) với $a \ge 0;b \ge 0$ ta được kết quả là
-
A.
$2\sqrt {2a} $
-
B.
$4\sqrt a $
-
C.
$8\sqrt a $
-
D.
$2\sqrt a $
Sau khi rút gọn biểu thức \(\dfrac{2}{{7 + 3\sqrt 5 }} + \dfrac{2}{{7 - 3\sqrt 5 }}\) là phân số tối giản \(\dfrac{a}{b},\left( {a,b \in \mathbb{Z}} \right)\). Khi đó \(a + b\) có giá trị là:
-
A.
\(28\)
-
B.
\(7\)
-
C.
\(8\)
-
D.
\(14\)
Cho \(P = \dfrac{{\sqrt x + 3}}{{\sqrt x - 2}}\) với \(x \ge 0;x \ne 4\). Có bao nhiêu giá trị \(x \in \mathbb{Z}\) để \(P \in \mathbb{Z}\).
-
A.
\(3\)
-
B.
\(2\)
-
C.
\(0\)
-
D.
\(4\)
Cho biểu thức \(A = \dfrac{{\sqrt x + 1}}{{\sqrt x - 2}}\) với \(x \ge 0;x \ne 4\). Tìm các giá trị của \(x\) biết \(A = \dfrac{{\sqrt x - 1}}{2}\) .
-
A.
\(x = 0;x = 5\)
-
B.
\(x = 0\)
-
C.
\(x = 0;x = 25\)
-
D.
\(x = 5;x = 1\)
Giải phương trình \(\sqrt {2{x^2} - 4x + 5} = x - 2\) ta được nghiệm là
-
A.
\(x = 1\)
-
B.
\(x = 3\)
-
C.
\(x = 2\)
-
D.
Phương trình vô nghiệm
Rút gọn biểu thức:$B = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}$ với \(x \ge 0;\,\,x \ne 4\).
-
A.
\(B = \dfrac{{\sqrt x }}{{\sqrt x + 2}}\)
-
B.
\(B = \dfrac{{\sqrt x }}{{\sqrt x - 2}}\)
-
C.
\(B = \dfrac{{ - \sqrt x }}{{\sqrt x - 2}}\)
-
D.
\(B = \dfrac{{2\sqrt x }}{{\sqrt x - 2}}\)
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH.$ Cho biết $AB:AC = 3:4$ và $AH = 6cm.$ Tính độ dài các đoạn thẳng $CH.$
-
A.
$CH = 8$
-
B.
$CH = 6$
-
C.
$CH = 10$
-
D.
$CH = 12$
Cho tam giác $ABC$ vuông tại $A$ có \(AB = 5\,cm,\,\,\cot C = \dfrac{7}{8}\) . Tính độ dài các đoạn thẳng $AC$ và $BC$ . (làm tròn đến chữ số thập phân thứ $2$ )
-
A.
$AC \approx 4,39 (cm);BC \approx 6,66 (cm)$
-
B.
$AC \approx 4,38(cm);BC \approx 6,64(cm)$
-
C.
$AC \approx 4,38(cm);BC \approx 6,67(cm)$
-
D.
$AC \approx 4,37(cm);BC \approx 6,67(cm)$
Cho $\alpha $ là góc nhọn bất kỳ. Biểu thức $Q = \dfrac{{1 + {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }}$ bằng
-
A.
$Q = 1 + {\tan ^2}\alpha $
-
B.
$Q = 1 + 2{\tan ^2}\alpha $
-
C.
$Q = 1 - 2{\tan ^2}\alpha $
-
D.
$Q = 2{\tan ^2}\alpha $
Nhà bạn Vũ có một chiếc thang dài \(3,5\,m\). Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn” là \({62^0}\) (tức là đảm bảo thang không bị đổ khi sử dụng). (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(1,65\,m\)
-
B.
\(1,64\,\,m\)
-
C.
\(1,68\,m\)
-
D.
\(1,69\,m\)
Tính số đo góc nhọn $x,$ biết: ${\cos ^2}x - {\sin ^2}x = \dfrac{1}{2}$
-
A.
\(45^\circ \)
-
B.
\(30^\circ \)
-
C.
\(60^\circ \)
-
D.
\(90^\circ \)
Cho \(\Delta ABC\) vuông tại \(A.\) Biết $\dfrac{{AB}}{{AC}} = \dfrac{5}{7}$. Đường cao $AH = 15cm.$ Tính ${\rm{ }}HC.$
-
A.
\(\dfrac{{15\sqrt {74} }}{7}\)
-
B.
\(3\sqrt {74} \,cm\)
-
C.
\(22\,cm\)
-
D.
\(21\,cm\)
Cho \(A = \dfrac{{2x}}{{x + 3\sqrt x + 2}} + \dfrac{{5\sqrt x + 1}}{{x + 4\sqrt x + 3}} + \dfrac{{\sqrt x + 10}}{{x + 5\sqrt x + 6}}\) với \(x \ge 0\). Chọn đáp án đúng.
-
A.
\(A = 2\sqrt x \)
-
B.
Giá trị của $A$ không phụ thuộc vào biến $x.$
-
C.
\(A = 3\left( {\sqrt x + 2} \right)\)
-
D.
\(A = \dfrac{2}{{\sqrt x + 1}}\)
Giả sử \(a;\,\,b;\,\,c\) là các số thực dương. Chọn câu đúng.
-
A.
$\sqrt {1 + {a^2}} + \sqrt {1 + {b^2}} + \sqrt {1 + {c^2}} \le 2\left( {\sqrt {a + b} + \sqrt {b + c} + \sqrt {c + a} } \right)$
-
B.
$\sqrt {1 + {a^2}} + \sqrt {1 + {b^2}} + \sqrt {1 + {c^2}} \ge 2\left( {\sqrt {a + b} + \sqrt {b + c} + \sqrt {c + a} } \right)$
-
C.
$\sqrt {1 + {a^2}} + \sqrt {1 + {b^2}} + \sqrt {1 + {c^2}} \le \sqrt {a + b} + \sqrt {b + c} + \sqrt {c + a} $
-
D.
$\sqrt {1 + {a^2}} + \sqrt {1 + {b^2}} + \sqrt {1 + {c^2}} \ge \sqrt {a + b} + \sqrt {b + c} + \sqrt {c + a} $
Lời giải và đáp án
Cho tam giác $MNP$ vuông tại $M$. Khi đó $\cos \widehat {MNP}$ bằng

-
A.
$\dfrac{{MN}}{{NP}}$
-
B.
$\dfrac{{MP}}{{NP}}$
-
C.
$\dfrac{{MN}}{{MP}}$
-
D.
$\dfrac{{MP}}{{MN}}$
Đáp án : A
Ta có $\cos \widehat {MNP} = \dfrac{{MN}}{{NP}}$
Một cột đèn có bóng trên mặt đất dài $7,5m.$ Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng ${42^0}.$ Tính chiều cao của cột đèn. (làm tròn đến chữ số thập phân thứ ba)
-
A.
$6,753\,m$
-
B.
$6,75\,m$
-
C.
$6,751\,m$
-
D.
$6,755\,m$
Đáp án : A
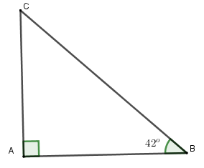
Ta có chiều cao cột đèn là $AC$; $AB = 7,5\,m$ và $\widehat {ACB} = 42^\circ $
Xét tam giác $ACB$ vuông tại $A$ có
$AC = AB.\tan B = 7,5.\tan 42^\circ \approx 6,753\,\,m$
Vậy cột đèn cao $6,753\,m$
Chọn câu đúng nhất. Nếu \(\alpha \) là một góc nhọn bất kỳ, ta có
-
A.
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
-
B.
\(\tan \alpha .\cot \alpha = 1\)
-
C.
\(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}\)
-
D.
Cả A, B, C đều đúng
Đáp án : D
Nếu \(\alpha \) là một góc nhọn bất kỳ thì \({\sin ^2}\alpha + {\cos ^2}\alpha = 1;\tan \alpha .\cot \alpha = 1\)
$\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }};\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }}$ nên cả A, B, C đều đúng
Cho \(B = \dfrac{2}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 3 - \sqrt 2 }} - \dfrac{2}{{\sqrt 3 - 1}}\) và \(C = \left( {2\sqrt 3 - 5\sqrt {27} + 4\sqrt {12} } \right):\sqrt 3 \). Chọn đáp án đúng.
-
A.
\(B > C\)
-
B.
\(B < C\)
-
C.
\(B = C\)
-
D.
\(B = - C\)
Đáp án : A
+ Tính \(B;C\) bằng cách sử dụng các công thức
Với \(A > 0\) và \(A \ne {B^2}\) thì \(\dfrac{C}{{\sqrt A \pm B}} = \dfrac{{C(\sqrt A \mp B)}}{{A - {B^2}}}\)
Khai phương một tích: \(\sqrt {A.B} = \sqrt A .\sqrt B {\rm{ }}(A \ge 0,B \ge 0)\)
+ So sánh \(B;C.\)
Ta có \(B = \dfrac{2}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 3 - \sqrt 2 }} - \dfrac{2}{{\sqrt 3 - 1}}\)
\( = \dfrac{{2\sqrt 2 }}{{\sqrt 2 .\sqrt 2 }} + \dfrac{{\sqrt 3 + \sqrt 2 }}{{\left( {\sqrt 3 - \sqrt 2 } \right)\left( {\sqrt 3 + \sqrt 2 } \right)}} - \dfrac{{2\left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}\)
$ = \dfrac{{2\sqrt 2 }}{2} + \dfrac{{\sqrt 3 + \sqrt 2 }}{{3 - 2}} - \dfrac{{2\left( {\sqrt 3 + 1} \right)}}{{3 - 1}}$ $= \sqrt 2 + \dfrac{{\sqrt 3 + \sqrt 2 }}{1} - \dfrac{{2\left( {\sqrt 3 + 1} \right)}}{2}$
\( = \sqrt 2 + \sqrt 3 + \sqrt 2 - \left( {\sqrt 3 + 1} \right)\)
\( = \sqrt 2 + \sqrt 3 + \sqrt 2 - \sqrt 3 - 1\)
\( = 2\sqrt 2 - 1\)
Lại có
$\begin{array}{l}C = (2\sqrt 3 - 5\sqrt {27} + 4\sqrt {12} ):\sqrt 3 \\ = \left( {2\sqrt 3 - 5\sqrt {9.3} + 4\sqrt {4.3} } \right):\sqrt 3 \\= (2\sqrt 3 - 5.3\sqrt 3 + 4.2\sqrt 3 ):\sqrt 3 \\ = - 5\sqrt 3 :\sqrt 3 \\ = - 5\end{array}$
Nhận thấy \(B = 2\sqrt 2 - 1 > 0;\,C = - 5 < 0 \Rightarrow B > C\)
Cho các biểu thức $A,B$ mà $A.B \ge 0;B > 0$, khẳng định nào sau đây là đúng?
-
A.
$\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt {AB} }}{B}$
-
B.
$\sqrt {\dfrac{A}{B}}=- \dfrac{{\sqrt {AB} }}{B}$
-
C.
$\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt A }}{B}$
-
D.
$\sqrt {\dfrac{A}{B}} = \dfrac{{AB}}{{\sqrt B }}$
Đáp án : A
Sử dụng công thức trục căn thức ở mẫu.
Sử dụng công thức trục căn thức ở mẫu.
Với các biểu thức $A,B$ mà $A.B \ge 0;B \ne 0$, ta có $\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt {AB} }}{{\left| B \right|}} = \left\{ \begin{array}{l}\dfrac{{\sqrt {AB} }}{B}\,\,khi\,B > 0\\ - \dfrac{{\sqrt {AB} }}{B}\,\,khi\,B < 0\end{array} \right.$
Cho tam giác $ABC$ vuông tại $A$ có $AB = 21\,cm$; $\widehat C = 40^\circ $ , phân giác \(BD\) (\(D\) thuộc \(AC\) ). Độ dài phân giác $BD$ là (Kết quả làm tròn đến chữ số thập phân thứ nhất)
-
A.
\(21,3\,cm\)
-
B.
\(24\,cm\)
-
C.
\(22,3\,cm\)
-
D.
\(23,2\,cm\)
Đáp án : D
+ Tính góc \(ABC\) từ đó suy ra góc \(ABD\)
+ Sử dụng hệ thức về cạnh và góc trong tam giác vuông \(ABD\) để tính \(BD.\)
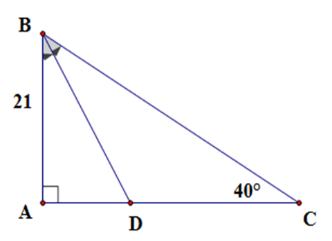
Xét tam giác \(ABC\) vuông tại \(A\) có \(\widehat {ABC} + \widehat C = 90^\circ \Rightarrow \widehat {ABC} = 50^\circ \)
Mà \(BD\) là phân giác góc \(ABC\) nên \(\widehat {ABD} = \dfrac{1}{2}\widehat {ABC} = 25^\circ \)
Xét tam giác \(ABD\) vuông tại \(A\) ta có \(BD = \dfrac{{AB}}{{\cos \widehat {ABD}}} = \dfrac{{21}}{{\cos 25^\circ }} \approx 23,2\,cm\)
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.
-
A.
$\sin \alpha + \cos \alpha = 1$
-
B.
${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
-
C.
${\sin ^3}\alpha + {\cos ^3}\alpha = 1$
-
D.
$\sin \alpha - cos\alpha = 1$
Đáp án : B
Từ tỉ số lượng giác sin, cos để chứng minh.
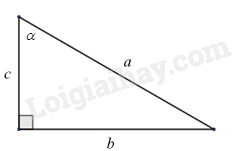
Giả sử ta có tam giác vuông có các cạnh và góc $\alpha $ như hình vẽ.
Áp dụng tỉ số lượng giác của góc nhọn, ta có:
$\sin \alpha =\frac{b}{a},\cos \alpha =\frac{c}{a},\tan \alpha =\frac{b}{c},\cot \alpha =\frac{c}{b}$.
Ta có: ${{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha ={{\left( \frac{b}{a} \right)}^{2}}+{{\left( \frac{c}{a} \right)}^{2}}=\frac{{{b}^{2}}+{{c}^{2}}}{{{a}^{2}}}=\frac{{{a}^{2}}}{{{a}^{2}}}=1$
Vậy ${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
Cho hình vẽ, tìm \(x.\)

-
A.
\(x = 0,75\)
-
B.
\(x = 4,5\)
-
C.
\(x = 4\sqrt 3 \)
-
D.
\(x = 4\)
Đáp án : B
Sử dụng hệ thức lượng trong tam giác vuông: “ bình phương cạnh góc vuông bằng tích hình chiếu của nó lên cạnh huyền với cạnh huyền”

Đặt tên như hình vẽ trên.
Tam giác \(MNP\) vuông tại \(M\) có \(MH \bot NP\)
Theo hệ thức lượng trong tam giác vuông ta có \(M{N^2} = N{H^2}.NP \Rightarrow {6^2} = x.8 \Rightarrow x = 36:8 = 4,5.\)
Vậy \(x = 4,5.\)
Khẳng định nào sau đây là đúng ?
-
A.
\(\sqrt {2018 + 2019} = \sqrt {2018} + \sqrt {2019} \)
-
B.
\(\sqrt {2018. 2019} = \dfrac{{\sqrt {2018} }}{{\sqrt {2019} }}\)
-
C.
\(\sqrt {2018} .\sqrt {2019} = \sqrt {2018.2019} \)
-
D.
\(2018. 2019 = \dfrac{{\sqrt {2019} }}{{\sqrt {2018} }}\)
Đáp án : C
Sử dụng công thức khai phương một tích: Với hai số \(a,b\) không âm, ta có \(\sqrt {ab} = \sqrt a .\sqrt b \)
Ta có: \(\sqrt {2018} .\sqrt {2019} = \sqrt {2018.2019} \)
Giá trị của biểu thức \(\sqrt {32} + \sqrt {50} - 3\sqrt 8 - \sqrt {18} \) là
-
A.
$1$
-
B.
$0$
-
C.
$2$
-
D.
$3$
Đáp án : B
-Sử dụng công thức khai phương một tích \(\sqrt {AB} = \sqrt A .\sqrt B ,\,\,\left( {A,B \ge 0} \right)\) đưa biểu thức về các căn thức cùng loại (cùng biểu thức dưới dấu căn).
-Cộng trừ các căn thức
\(\sqrt {32} + \sqrt {50} - 3\sqrt 8 - \sqrt {18} \)\( = \sqrt {16.2} + \sqrt {25.2} - 3\sqrt {4.2} - \sqrt {9.2} \)
\(= 4\sqrt 2 + 5\sqrt 2 - 6\sqrt 2 - 3\sqrt 2 = 0\)
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là đúng ?

-
A.
$A{H^2} = AB.AC$
-
B.
$A{H^2} = BH.CH$
-
C.
$A{H^2} = AB.BH$
-
D.
$A{H^2} = CH.BC$
Đáp án : B
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ . Khi đó ta có hệ thức $H{A^2} = HB.HC$
Tính \(x\) trong hình vẽ sau:

-
A.
\(x = 14\)
-
B.
\(x = 13\)
-
C.
\(x = 12\)
-
D.
\(x = \sqrt {145} \)
Đáp án : C
Tính \(x\) theo hệ thức lượng \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)\( \Rightarrow AH = \dfrac{{AB.AC}}{{\sqrt {A{B^2} + A{C^2}} }} = \dfrac{{15.20}}{{\sqrt {{{15}^2} + {{20}^2}} }} = 12\)
Vậy \(x = 12\).
Tìm các số $x$ không âm thỏa mãn $\sqrt x \ge 3$
-
A.
$x \ge 9$
-
B.
$x < 9$
-
C.
$x > 9$
-
D.
$x \le 9$
Đáp án : A
Sử dụng cách so sánh hai căn bậc hai $\sqrt A > \sqrt B \Leftrightarrow A > B$ với $A,B$ không âm.
Vì $3 = \sqrt 9 $ nên $\sqrt x \ge 3$ được viết là $\sqrt x \ge \sqrt 9 $. Vì $x$ không âm nên $\sqrt x \ge \sqrt 9 $$ \Rightarrow x \ge 9$.
So sánh hai số \(5\) và \(\sqrt {50} - 2\).
-
A.
\(5 > \sqrt {50} - 2\)
-
B.
\(5 = \sqrt {50} - 2\)
-
C.
\(5 < \sqrt {50} - 2\)
-
D.
Chưa đủ điều kiện để so sánh.
Đáp án : C
So sánh hai căn bậc hai: Với hai số \(a,b\) không âm ta có \(a < b \Leftrightarrow \sqrt a < \sqrt b \).
Tách \(5 = 7 - 2 = \sqrt {49} - 2\).
Vì \(49 < 50 \) nên \( \sqrt {49} < \sqrt {50} \)
\( 7 < \sqrt {50} \)
\(7 - 2 < \sqrt {50} - 2 \)
\( 5 < \sqrt {50} - 2\).
So sánh hai số \(9\sqrt 7 \) và \(8\sqrt 8 \)
-
A.
\(8\sqrt 8 < 9\sqrt 7 \)
-
B.
\(8\sqrt 8 = 9\sqrt 7 \)
-
C.
\(8\sqrt 8 \ge 9\sqrt 7 \)
-
D.
\(9\sqrt 7 < 8\sqrt 8 \)
Đáp án : A
Đưa thừa số vào trong dấu căn để so sánh hai số \(\sqrt A < \sqrt B \Leftrightarrow 0 \le A < B\).
Đưa thừa số vào trong dấu căn
+) \(A\sqrt B = \sqrt {{A^2}B} \) với \(A \ge 0\) và \(B \ge 0\)
+) \(A\sqrt B = - \sqrt {{A^2}B} \) với \(A < 0\) và \(B \ge 0\)
Ta có: \(9\sqrt 7 = \sqrt {{9^2}.7} = \sqrt {81.7} = \sqrt {567} \); \(8\sqrt 8 = \sqrt {{8^2}.8} = \sqrt {64.8} = \sqrt {512} \)
Vì \(512 < 567 \) nên \( \sqrt {512} < \sqrt {567} \) hay \(8\sqrt 8 < 9\sqrt 7 \)
Tìm điều kiện của $x$ để căn thức \(\sqrt {\dfrac{1}{{x - 1}}} \) có nghĩa.
-
A.
$x \ge 1$
-
B.
\(x < 1\)
-
C.
\(x > 1\)
-
D.
\(x = 1\)
Đáp án : C
\(\sqrt A \) xác định (hay có nghĩa) khi \(A\) lấy giá trị không âm tức là \(A \ge 0.\)
Ngoài ra: \(\dfrac{1}{A} \ge 0 \Leftrightarrow A > 0\)
Ta có \(\sqrt {\dfrac{1}{{x - 1}}} \) có nghĩa \( \Leftrightarrow \dfrac{1}{{x - 1}} \ge 0 \Rightarrow x - 1 > 0\) (vì $1>0$)
\( \Leftrightarrow x > 1\)
Rút gọn biểu thức
$\sqrt {{a^2} + 8a + 16} + \sqrt {{a^2} - 8a + 16} $ với $ - 4 \le a \le 4$ ta được
-
A.
$2a$
-
B.
$8$
-
C.
$ - 8$
-
D.
$ - 2a$
Đáp án : B
-Đưa biểu thức dưới dấu căn thành hằng đẳng thức ${\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}$ và ${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$.
-Sử dụng hằng đẳng thức $\sqrt {{A^2}} = \left| A \right|$
- Phá dấu giá trị tuyệt đối $\left| A \right| = \left\{ \begin{array}{l}A\,\,khi\,A \ge 0\\ - A\,\,\,khi\,A < 0\end{array} \right.$ (dựa vào điều kiện đề bài).
Ta có $\sqrt {{a^2} + 8a + 16} = \sqrt {{{\left( {a + 4} \right)}^2}} = \left| {a + 4} \right|$.
Mà $ - 4 \le a \le 4 \Rightarrow a + 4 \ge 0$
$\Rightarrow \left| {a + 4} \right| = a + 4$
Hay $\sqrt {{a^2} + 8a + 16} = a + 4$ với $ - 4 \le a \le 4$
Ta có $\sqrt {{a^2} - 8a + 16} = \sqrt {{{\left( {a - 4} \right)}^2}} $
$= \left| {a - 4} \right|$.
Mà $ - 4 \le a \le 4 \Rightarrow a - 4 \le 0 $
$\Rightarrow \left| {a - 4} \right| = 4 - a$
Hay $\sqrt {{a^2} - 8a + 16} = 4 - a$ với $ - 4 \le a \le 4$
Khi đó $\sqrt {{a^2} + 8a + 16} + \sqrt {{a^2} - 8a + 16} $
$= a + 4 + 4 - a = 8$.
Giá trị của biểu thức \(\sqrt {252} - \sqrt {700} + \sqrt {1008} - \sqrt {448} \) là:
-
A.
\(\sqrt 7 \)
-
B.
\(0\)
-
C.
\(4\sqrt 7 \)
-
D.
\(5\sqrt 7 \)
Đáp án : B
- Sử dụng công thức khai phương một tích: Với hai số \(a,b\) không âm, ta có \(\sqrt {ab} = \sqrt a .\sqrt b \).
Ta có: \(\sqrt {252} - \sqrt {700} + \sqrt {1008} - \sqrt {448} \)\( = \sqrt {36.7} - \sqrt {100.7} + \sqrt {144.7} - \sqrt {64.7} \)\( = \sqrt {36} .\sqrt 7 - \sqrt {100} .\sqrt 7 + \sqrt {144} .\sqrt 7 - \sqrt {64} .\sqrt 7 = 6\sqrt 7 - 10\sqrt 7 + 12\sqrt 7 - 8\sqrt 7 = \sqrt 7 \left( {6 - 10 + 12 - 8} \right) = 0\)
Rút gọn biểu thức \(5\sqrt a - 4b\sqrt {25{a^3}} + 5a\sqrt {16a{b^2}} - \sqrt {9a} \) với $a \ge 0;b \ge 0$ ta được kết quả là
-
A.
$2\sqrt {2a} $
-
B.
$4\sqrt a $
-
C.
$8\sqrt a $
-
D.
$2\sqrt a $
Đáp án : D
Sử dụng công thức đưa thừa số vào trong dấu căn và công thức khai phương một tích để xuất hiện nhân tử chung từ đó thực hiện phép tính.
Đưa thừa số vào trong dấu căn
+) $A\sqrt B = \sqrt {{A^2}B} $ với $A \ge 0$ và $B \ge 0$
+) $A\sqrt B = - \sqrt {{A^2}B} $ với $A < 0$ và $B \ge 0$
Công thức khai phương một tích
$\sqrt {AB} = \sqrt A .\sqrt B \,\,\left( {A \ge 0;B \ge 0} \right)$
Ta có \(5\sqrt a - 4b\sqrt {25{a^3}} + 5a\sqrt {16a{b^2}} - \sqrt {9a} \)$ = 5\sqrt a - 4\sqrt {25{a^3}{b^2}} + 5\sqrt {16a{b^2}.{a^2}} - \sqrt 9 .\sqrt a $
$ = 5\sqrt a - 4\sqrt {25} .\sqrt {{a^3}{b^2}} + 5\sqrt {16} .\sqrt {{a^3}{b^2}} - 3\sqrt a $$ = \left( {5\sqrt a - 3\sqrt a } \right) - \left( {4.5\sqrt {{a^3}{b^2}} - 5.4\sqrt {{a^3}{b^2}} } \right)$$ = 2\sqrt a $
Sau khi rút gọn biểu thức \(\dfrac{2}{{7 + 3\sqrt 5 }} + \dfrac{2}{{7 - 3\sqrt 5 }}\) là phân số tối giản \(\dfrac{a}{b},\left( {a,b \in \mathbb{Z}} \right)\). Khi đó \(a + b\) có giá trị là:
-
A.
\(28\)
-
B.
\(7\)
-
C.
\(8\)
-
D.
\(14\)
Đáp án : C
Trục căn thức ở mẫu theo công thức
Với các biểu thức \(A,B,C\) mà \(A \ge 0,A \ne {B^2}\), ta có \(\dfrac{C}{{\sqrt A + B}} = \dfrac{{C\left( {\sqrt A - B} \right)}}{{A - {B^2}}};\dfrac{C}{{\sqrt A - B}} = \dfrac{{C\left( {\sqrt A + B} \right)}}{{A - {B^2}}}\)
Ta có: \(\dfrac{2}{{7 + 3\sqrt 5 }} + \dfrac{2}{{7 - 3\sqrt 5 }} = \dfrac{{2\left( {7 - 3\sqrt 5 } \right)}}{{\left( {7 + 3\sqrt 5 } \right)\left( {7 - 3\sqrt 5 } \right)}} + \dfrac{{2\left( {7 + 3\sqrt 5 } \right)}}{{\left( {7 - 3\sqrt 5 } \right)\left( {7 + 3\sqrt 5 } \right)}}\)
\( = \dfrac{{14 - 6\sqrt 5 }}{{{7^2} - {{\left( {3\sqrt 5 } \right)}^2}}} + \dfrac{{14 + 6\sqrt 5 }}{{{7^2} - {{\left( {3\sqrt 5 } \right)}^2}}} = \dfrac{{14 - 6\sqrt 5 + 14 + 6\sqrt 5 }}{{49 - 9.5}} = \dfrac{{28}}{4} = \dfrac{7}{1}\)
Suy ra \(a = 7;b = 1 \Rightarrow a + b = 7 + 1 = 8\).
Cho \(P = \dfrac{{\sqrt x + 3}}{{\sqrt x - 2}}\) với \(x \ge 0;x \ne 4\). Có bao nhiêu giá trị \(x \in \mathbb{Z}\) để \(P \in \mathbb{Z}\).
-
A.
\(3\)
-
B.
\(2\)
-
C.
\(0\)
-
D.
\(4\)
Đáp án : A
Sử dụng: với \(P = \dfrac{a}{b}\) với \(a,b \in \mathbb{Z}\) thì \(P \in \mathbb{Z} \) khi \( a\, \vdots \,b\)
TH1: \(\sqrt x \) là số vô tỉ thì \(\dfrac{{\sqrt x + 3}}{{\sqrt x - 2}}\) là số vô tỉ hay \(P\) là số vô tỉ (loại).
TH2: \(\sqrt x \) là số nguyên.
Ta có: \(P = \dfrac{{\sqrt x + 3}}{{\sqrt x - 2}} = \dfrac{{\sqrt x - 2 + 5}}{{\sqrt x - 2}} \)\(= \dfrac{{\sqrt x - 2}}{{\sqrt x - 2}} + \dfrac{5}{{\sqrt x - 2}} = 1 + \dfrac{5}{{\sqrt x - 2}}\)
Vì \(1 \in \mathbb{Z}\) nên để \(P = 1 + \dfrac{5}{{\sqrt x - 2}}\) nhận giá trị nguyên thì \(\dfrac{5}{{\sqrt x - 2}} \in \mathbb{Z}\) hay \(5 \,\vdots \,\left( {\sqrt x - 2} \right) \\\left( {\sqrt x - 2} \right) \in Ư\left( 5 \right) = \left\{ {1; - 1;5; - 5} \right\}\)
+) \(\sqrt x - 2 = 1 \) \( \sqrt x = 3 \\x = 9\left( {tm} \right)\)
+) \(\sqrt x - 2 = - 1 \) \( \sqrt x = 1 \\ x = 1\left( {tm} \right)\)
+) \(\sqrt x - 2 = 5 \) \( \sqrt x = 7 \\ x = 49\left( {tm} \right)\)
+) \(\sqrt x - 2 = - 5 \) \( \sqrt x = - 3\) (vô nghiệm vì \(\sqrt x \ge 0\) với mọi \( x \ge 0\))
Vậy có ba giá trị của \(x\) thỏa mãn điều kiện là \(x = 1;x = 9;x = 49\).
Cho biểu thức \(A = \dfrac{{\sqrt x + 1}}{{\sqrt x - 2}}\) với \(x \ge 0;x \ne 4\). Tìm các giá trị của \(x\) biết \(A = \dfrac{{\sqrt x - 1}}{2}\) .
-
A.
\(x = 0;x = 5\)
-
B.
\(x = 0\)
-
C.
\(x = 0;x = 25\)
-
D.
\(x = 5;x = 1\)
Đáp án : C
Cho \(A = \dfrac{{\sqrt x - 1}}{2}\)
Giải phương trình chứa căn bằng cách quy đồng mẫu số, đưa phương trình về dạng chứa căn cơ bản đã biết.
Với \(x \ge 0;x \ne 4\) ta có: \(A = \dfrac{{\sqrt x - 1}}{2} \\ \dfrac{{\sqrt x + 1}}{{\sqrt x - 2}} = \dfrac{{\sqrt x - 1}}{2}\)
\( \Rightarrow 2\left( {\sqrt x + 1} \right) = \left( {\sqrt x - 2} \right)\left( {\sqrt x - 1} \right) \\ 2\sqrt x + 2 = x - 3\sqrt x + 2\)
\( \\ x - 5\sqrt x = 0 \\ \sqrt x \left( {\sqrt x - 5} \right) = 0 \\ \left[ \begin{array}{l}\sqrt x = 0\\\sqrt x = 5\end{array} \right. \\ \left[ \begin{array}{l}x = 0\left( {tm} \right)\\x = 25\left( {tm} \right)\end{array} \right.\)
Vậy giá trị cần tìm là \(x = 0;x = 25\).
Giải phương trình \(\sqrt {2{x^2} - 4x + 5} = x - 2\) ta được nghiệm là
-
A.
\(x = 1\)
-
B.
\(x = 3\)
-
C.
\(x = 2\)
-
D.
Phương trình vô nghiệm
Đáp án : D
+ Tìm điều kiện
+ Giải phương trình dạng \(\sqrt A = B\,\left( {B \ge 0} \right) \Leftrightarrow A = {B^2}\)
Điều kiện:
\(x - 2 \ge 0 \Leftrightarrow x \ge 2.\)
Ta có: \(\sqrt {2{x^2} - 4x + 5} = x - 2\)\( \Leftrightarrow 2{x^2} - 4x + 5 = {\left( {x - 2} \right)^2}\)
\( \Leftrightarrow 2{x^2} - 4x + 5 = {x^2} - 4x + 4 \Leftrightarrow {x^2} + 1 = 0\) \( \Leftrightarrow {x^2} = - 1\,\) (vô nghiệm vì \({x^2} \ge 0\,\,\forall x\) )
Vậy phương trình vô nghiệm.
Rút gọn biểu thức:$B = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}$ với \(x \ge 0;\,\,x \ne 4\).
-
A.
\(B = \dfrac{{\sqrt x }}{{\sqrt x + 2}}\)
-
B.
\(B = \dfrac{{\sqrt x }}{{\sqrt x - 2}}\)
-
C.
\(B = \dfrac{{ - \sqrt x }}{{\sqrt x - 2}}\)
-
D.
\(B = \dfrac{{2\sqrt x }}{{\sqrt x - 2}}\)
Đáp án : B
+ Phân tích mẫu thức thành nhân tử rồi qui đồng mẫu các phân thức
+ Từ đó rút gọn phân thức
$\begin{array}{l}B = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}} = \dfrac{x}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\\\,\,\,\,\, = \dfrac{{x + \sqrt x + 2 + \sqrt x - 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} = \dfrac{{x + 2\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\\\,\,\,\,\, = \dfrac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} = \dfrac{{\sqrt x }}{{\sqrt x - 2}}.\end{array}$
Vậy \(B = \dfrac{{\sqrt x }}{{\sqrt x - 2}}\) với \(x \ge 0;\,\,x \ne 4\).
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH.$ Cho biết $AB:AC = 3:4$ và $AH = 6cm.$ Tính độ dài các đoạn thẳng $CH.$
-
A.
$CH = 8$
-
B.
$CH = 6$
-
C.
$CH = 10$
-
D.
$CH = 12$
Đáp án : A
Bước 1: Tính $AB,AC$ dựa vào tỉ lệ cho trước và hệ thức $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
Bước 2: Tính $CH$ theo định lý Pytago
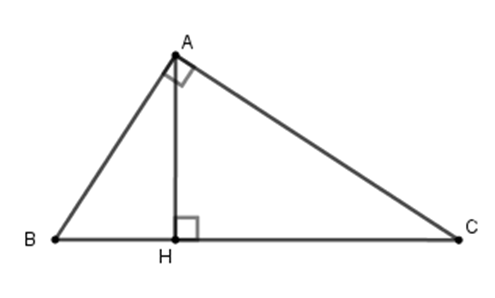
Ta có $AB:AC = 3:4$ , đặt $AB = 3a;AC = 4a\,\left( {a > 0} \right)$
Theo hệ thức lượng $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$$ \Rightarrow \dfrac{1}{{36}} = \dfrac{1}{{9{a^2}}} + \dfrac{1}{{16{a^2}}} \Rightarrow \dfrac{1}{{36}} = \dfrac{{25}}{{144{a^2}}} \Rightarrow a = \dfrac{5}{2}$ (TM )
$ \Rightarrow AB = 7,5;AC = 10$
Theo định lý Pytago cho tam giác vuông $AHC$ ta có $CH = \sqrt {A{C^2} - A{H^2}} = \sqrt {100 - 36} = 8$
Vậy $CH = 8$ .
Cho tam giác $ABC$ vuông tại $A$ có \(AB = 5\,cm,\,\,\cot C = \dfrac{7}{8}\) . Tính độ dài các đoạn thẳng $AC$ và $BC$ . (làm tròn đến chữ số thập phân thứ $2$ )
-
A.
$AC \approx 4,39 (cm);BC \approx 6,66 (cm)$
-
B.
$AC \approx 4,38(cm);BC \approx 6,64(cm)$
-
C.
$AC \approx 4,38(cm);BC \approx 6,67(cm)$
-
D.
$AC \approx 4,37(cm);BC \approx 6,67(cm)$
Đáp án : B
Sử dụng tỉ số lương giác của góc nhọn, định lý Pytago để tính cạnh.
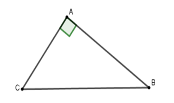
Vì tam giác $ABC$ vuông tại $A$ nên $\cot C = \dfrac{{AC}}{{AB}} \Rightarrow AC = AB.\cot C = 5.\dfrac{7}{8} = \dfrac{{35}}{8} \approx 4,38\,\,cm$
Theo định lý Pytago ta có \(B{C^2} = A{B^2} + A{C^2} = {5^2} + {\left( {\dfrac{{35}}{8}} \right)^2} \Rightarrow BC \approx 6,64\)
Vậy $AC \approx 4,38(cm);BC \approx 6,64(cm)$.
Cho $\alpha $ là góc nhọn bất kỳ. Biểu thức $Q = \dfrac{{1 + {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }}$ bằng
-
A.
$Q = 1 + {\tan ^2}\alpha $
-
B.
$Q = 1 + 2{\tan ^2}\alpha $
-
C.
$Q = 1 - 2{\tan ^2}\alpha $
-
D.
$Q = 2{\tan ^2}\alpha $
Đáp án : B
Biến đổi để sử dụng các đẳng thức lượng giác thích hợp.
Với $\tan \alpha = \dfrac{{sin\alpha }}{{\cos \alpha }};{\cos ^2}\alpha = 1 - {\sin ^2}\alpha $.
$Q = \dfrac{{1 + {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }}$$ = \dfrac{{1 - {{\sin }^2}\alpha + 2{{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }} = \dfrac{{1 - {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }} + \dfrac{{2{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}$
$ = 1 + 2.{\left( {\dfrac{{\sin \alpha }}{{\cos \alpha }}} \right)^2} = 1 + 2{\tan ^2}\alpha $
Vậy $Q = 1 + 2{\tan ^2}\alpha $.
Nhà bạn Vũ có một chiếc thang dài \(3,5\,m\). Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn” là \({62^0}\) (tức là đảm bảo thang không bị đổ khi sử dụng). (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(1,65\,m\)
-
B.
\(1,64\,\,m\)
-
C.
\(1,68\,m\)
-
D.
\(1,69\,m\)
Đáp án : B
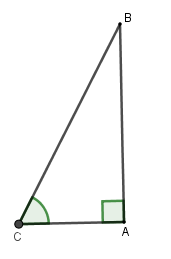
Ta có \(BC = 3,5\,\,m;\widehat C = 62^\circ \). Xét \(\Delta ABC\) vuông tại \(A\) có \(AC = BC.\cos \widehat C = 3,5.\cos 62^\circ \simeq 1,64\,\,m\).
Tính số đo góc nhọn $x,$ biết: ${\cos ^2}x - {\sin ^2}x = \dfrac{1}{2}$
-
A.
\(45^\circ \)
-
B.
\(30^\circ \)
-
C.
\(60^\circ \)
-
D.
\(90^\circ \)
Đáp án : B
Áp dụng hệ thức \({\sin ^2}x + {\cos ^2}x = 1\) để biến đổi giả thiết
Ta có \({\sin ^2}x + {\cos ^2}x = 1\) \( \Rightarrow {\sin ^2}x = 1 - {\cos ^2}x\)
Từ đó ${\cos ^2}x - {\sin ^2}x = \dfrac{1}{2}$
\( \Leftrightarrow {\cos ^2}x - \left( {1 - {{\cos }^2}x} \right) = \dfrac{1}{2} \Leftrightarrow 2{\cos ^2}x = \dfrac{3}{2}\) \( \Leftrightarrow {\cos ^2}x = \dfrac{3}{4} \Rightarrow \cos x = \dfrac{{\sqrt 3 }}{2}\) (do \(x\) là góc nhọn nên \(\cos x > 0\) )
Suy ra \(x = 30^\circ .\)
Cho \(\Delta ABC\) vuông tại \(A.\) Biết $\dfrac{{AB}}{{AC}} = \dfrac{5}{7}$. Đường cao $AH = 15cm.$ Tính ${\rm{ }}HC.$
-
A.
\(\dfrac{{15\sqrt {74} }}{7}\)
-
B.
\(3\sqrt {74} \,cm\)
-
C.
\(22\,cm\)
-
D.
\(21\,cm\)
Đáp án : D
Đặt \(AB = 5a;AC = 7a\) \(\left( {a > 0} \right)\)
Sử dụng hệ thức lượng trong tam giác vuông một cách thích hợp để tìm \(HC.\)
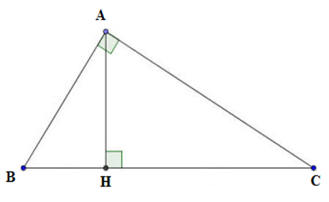
Vì \(\dfrac{{AB}}{{AC}} = \dfrac{5}{7} \Rightarrow AB = 5a;AC = 7a\) với \(a > 0.\)
Theo hệ thức lượng trong tam giác \(ABC\) vuông tại \(A\) ta có
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)
\( \Leftrightarrow \dfrac{1}{{{{15}^2}}} = \dfrac{1}{{{{\left( {5a} \right)}^2}}} + \dfrac{1}{{{{\left( {7a} \right)}^2}}}\) \( \Leftrightarrow \dfrac{1}{{225}} = \dfrac{1}{{25{a^2}}} + \dfrac{1}{{49{a^2}}} \Leftrightarrow \dfrac{1}{{225}} = \dfrac{{74}}{{1225{a^2}}} \Rightarrow {a^2} = \dfrac{{666}}{{49}} \Rightarrow a = \dfrac{{3\sqrt {74} }}{7}\)
Suy ra \(AB = \dfrac{{15\sqrt {74} }}{7};AC = 3\sqrt {74} \)
Lại có \(AH.BC = AB.AC \Rightarrow BC = \dfrac{{AB.AC}}{{AH}} = \dfrac{{222}}{7}\)
Mà \(A{C^2} = CH.BC \Rightarrow HC = \dfrac{{A{C^2}}}{{BC}} = 21\,cm.\)
Cho \(A = \dfrac{{2x}}{{x + 3\sqrt x + 2}} + \dfrac{{5\sqrt x + 1}}{{x + 4\sqrt x + 3}} + \dfrac{{\sqrt x + 10}}{{x + 5\sqrt x + 6}}\) với \(x \ge 0\). Chọn đáp án đúng.
-
A.
\(A = 2\sqrt x \)
-
B.
Giá trị của $A$ không phụ thuộc vào biến $x.$
-
C.
\(A = 3\left( {\sqrt x + 2} \right)\)
-
D.
\(A = \dfrac{2}{{\sqrt x + 1}}\)
Đáp án : B
+ Phân tích mẫu thức thành nhân tử rồi qui đồng mẫu các phân thức
+ Từ đó rút gọn phân thức
$A = \dfrac{{2x}}{{x + 3\sqrt x + 2}} + \dfrac{{5\sqrt x + 1}}{{x + 4\sqrt x + 3}} + \dfrac{{\sqrt x + 10}}{{x + 5\sqrt x + 6}}$$= \dfrac{{2x}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)}} + \dfrac{{5\sqrt x + 1}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 3} \right)}} + \dfrac{{\sqrt x + 10}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}$
\( = \dfrac{{2x\left( {\sqrt x + 3} \right) + \left( {5\sqrt x + 1} \right)\left( {\sqrt x + 2} \right) + \left( {\sqrt x + 10} \right)\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\)
\( = \dfrac{{2x\sqrt x + 6x + 5x + 11\sqrt x + 2 + x + 11\sqrt x + 10}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\)
\( = \dfrac{{2x\sqrt x + 12x + 22\sqrt x + 12}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\)
\( = \dfrac{{2x\sqrt x + 2x + 10x + 10\sqrt x + 12\sqrt x + 12}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\)
\(\begin{array}{l} = \dfrac{{2x\left( {\sqrt x + 1} \right) + 10\sqrt x \left( {\sqrt x + 1} \right) + 12\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\\ = \dfrac{{\left( {\sqrt x + 1} \right)\left( {2x + 10\sqrt x + 12} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\\ = \dfrac{{2\left( {x + 5\sqrt x + 6} \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\\ = \dfrac{{2\left( {x + 2\sqrt x + 3\sqrt x + 6} \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\\ = \dfrac{{2\left[ {\sqrt x \left( {\sqrt x + 2} \right) + 3\left( {\sqrt x + 2} \right)} \right]}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\\= \dfrac{{2\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\\ = 2\end{array}\)
Vậy giá trị của $A$ không phụ thuộc vào biến $x.$
Giả sử \(a;\,\,b;\,\,c\) là các số thực dương. Chọn câu đúng.
-
A.
$\sqrt {1 + {a^2}} + \sqrt {1 + {b^2}} + \sqrt {1 + {c^2}} \le 2\left( {\sqrt {a + b} + \sqrt {b + c} + \sqrt {c + a} } \right)$
-
B.
$\sqrt {1 + {a^2}} + \sqrt {1 + {b^2}} + \sqrt {1 + {c^2}} \ge 2\left( {\sqrt {a + b} + \sqrt {b + c} + \sqrt {c + a} } \right)$
-
C.
$\sqrt {1 + {a^2}} + \sqrt {1 + {b^2}} + \sqrt {1 + {c^2}} \le \sqrt {a + b} + \sqrt {b + c} + \sqrt {c + a} $
-
D.
$\sqrt {1 + {a^2}} + \sqrt {1 + {b^2}} + \sqrt {1 + {c^2}} \ge \sqrt {a + b} + \sqrt {b + c} + \sqrt {c + a} $
Đáp án : D
Bài toán kết hợp cả hai bất đẳng thức quen thuộc là Cosi và Bunhiacopxki để chứng minh bất đẳng thức.
Nhắc lại kiến thức và phương pháp:
+ Bất đẳng thức Cosi cho hai số thực dương: $a + b \ge 2\sqrt {ab} $.
+ Bất đẳng thức Bunhiacopxki cho hai bộ số $(a;\,\,b);\,\,(c;\,\,d)$ ta có ${\left( {ac + bd} \right)^2} \le \left( {{a^2} + {b^2}} \right)\left( {{c^2} + {d^2}} \right)$.
Theo bất đẳng thức Cô si:
$\sqrt {1 + {a^2}} + \sqrt {1 + {b^2}} \ge 2\sqrt {\sqrt {1 + {a^2}} \sqrt {1 + {b^2}} } = 2\sqrt[4]{(1 + {a^2}) (1 + {b^2})}.$
Theo bất đẳng thức Bunhia cốpxki:
\(\left( {1 + {a^2}} \right)\left( {1 + {b^2}} \right) = \left( {1 + {a^2}} \right)\left( {{b^2} + 1} \right) \ge {(a + b)^2}\)
$ \Rightarrow \sqrt {1 + {a^2}} + \sqrt {1 + {b^2}} \ge 2\sqrt {a + b} $
Tương tự: $\sqrt {1 + {b^2}} + \sqrt {1 + {c^2}} \ge 2\sqrt {b + c} $$ \Rightarrow \sqrt {1 + {c^2}} + \sqrt {1 + {a^2}} \ge 2\sqrt {c + a} $
Cộng cả ba bất đẳng thức trên rồi chia cho 2 ta có:
\(\sqrt {1 + {a^2}} + \sqrt {1 + {b^2}} + \sqrt {1 + {c^2}} \ge \sqrt {a + b} + \sqrt {b + c} + \sqrt {c + a} \)
Dấu “=” xảy ra khi \(a = b = c = 1.\)