Đề kiểm tra 45 phút chương 6: Đường tròn - Đề số 2
Đề bài
Cho đường tròn \(\left( O \right)\)có hai dây \(AB,CD\) không đi qua tâm. Biết rằng khoảng cách từ tâm \(O\) đến dây \(AB\) lớn hơn khoảng cách từ tâm \(O\) đến dây \(CD\). Kết luận nào sau đây là đúng?
-
A.
\(AB > CD\)
-
B.
\(AB = CD\)
-
C.
\(AB < CD\)
-
D.
\(AB{\rm{//}}CD\)
Cho \(\left( {O;4cm} \right)\). Đường thẳng \(d\) là tiếp tuyến của đường tròn \(\left( {O;4\,cm} \right)\), khi đó
-
A.
Khoảng cách từ \(O\) đến đường thẳng \(d\) nhỏ hơn \(4\,cm\)
-
B.
Khoảng cách từ \(O\) đến đường thẳng \(d\) bằng \(4\,cm\)
-
C.
Khoảng cách từ \(O\) đến đường thẳng \(d\) lớn hơn \(4\,cm\)
-
D.
Khoảng cách từ \(O\) đến đường thẳng \(d\) bằng \(5\,cm\)
Cho đường tròn $\left( O \right)$ có bán kính $R = 5\,cm$. Khoảng cách từ tâm đến dây $AB$ là $3\,cm$. Tính độ dài dây $AB$.
-
A.
$AB = 6\,cm$
-
B.
$AB = 8\,cm$
-
C.
$AB = 10\,cm$
-
D.
$AB = 12\,cm$
Cho đường tròn \(\left( O \right)\) và điểm \(A\) nằm trên đường tròn \(\left( O \right).\) Nếu đường thẳng \(d \bot OA\) tại \(A\) thì
-
A.
\(d\) là tiếp tuyến của \(\left( O \right)\)
-
B.
\(d\) cắt \(\left( O \right)\) tại hai điểm phân biệt
-
C.
\(d\) là tiếp xúc với \(\left( O \right)\) tại \(O\)
-
D.
Cả A, B, C đều sai
Đường tròn là hình:
-
A.
Không có trục đối xứng
-
B.
Có một trục đối xứng
-
C.
Có hai trục đối xứng
-
D.
Có vô số trục đối xứng
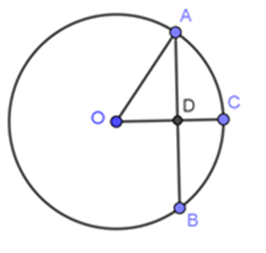
Trong hình vẽ bên cho $OC \bot AB,AB = 12cm,OA = 10cm$. Độ dài $AC$ là:
-
A.
$8cm$
-
B.
$2\sqrt {10} cm$
-
C.
$4\sqrt 7 cm$
-
D.
$2cm$
Cho đường tròn $\left( {O;3cm} \right)$, lấy điểm $A$ sao cho $OA = 6cm$. Từ \(A\) vẽ tiếp tuyến $AB,AC$ đến đường tròn $\left( O \right)$ ($B,C$ là tiếp điểm). Chu vi tam giác $ABC$ là
-
A.
$9cm$
-
B.
$9\sqrt 3 cm$
-
C.
$9\sqrt 2 cm$
-
D.
Kết quả khác
Từ một điểm $A$ ở bên ngoài đường tròn $\left( {O;R} \right)$,vẽ hai tiếp tuyến $AB,AC$ với $\left( O \right)$. Đường thẳng vuông góc với $OB$ tại $O$ cắt tia $AC$ tại $N$. Đường thẳng vuông góc với $OC$ tại $O$ cắt tia $AB$ tại $M$.
Điểm $A$ phải cách $O$ một khoảng là bao nhiêu để cho $MN$ là tiếp tuyến của $\left( O \right)$?
-
A.
$OA = 2R$
-
B.
$OA = \dfrac{3}{2}R$
-
C.
$OA = 3R$
-
D.
$OA = \dfrac{4}{3}R$
T ứ giác $AMON$ là hình gì?
-
A.
H ình bình hành
-
B.
H ình thoi
-
C.
H ình thang
-
D.
H ình chữ nhật
Cho nửa đường tròn tâm $O$ đường kính $AB.$ Vẽ các tiếp tuyến $Ax$ và $By$ ($Ax$ và $By$ và nửa đường tròn cùng thuộc về một nửa mặt phẳng bờ là $AB$ ). Gọi $M$ là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại $M$ cắt $Ax$ và $By$ theo thứ tự tại $C$ và $D.$ Lấy $I$ là trung điểm của $CD.$
Chọn câu sai.
-
A.
Đường tròn có đường kính $CD$ tiếp xúc với $AB.$
-
B.
Đường tròn có đường kính $CD$ cắt $AB.$
-
C.
$IO\; \bot AB$
-
D.
\(IO = \dfrac{{DC}}{2}\)
Hình thang $ABDC$ có chu vi nhỏ nhất là
-
A.
\(AB\)
-
B.
\(2AB\)
-
C.
\(3AB\)
-
D.
\(4AB\)
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Đường tròn đường kính $BH$ cắt $AB$ tại $D$, đường tròn đường kính $CH$ cắt $AC$ tại $E$ . Chọn khẳng định sai trong các khẳng định sau
-
A.
$DE$ là cát tuyến của đường tròn đường kính $BH$
-
B.
$DE$ là tiếp tuyến của đường tròn đường kính $BH$
-
C.
Tứ giác$AEHD$ là hình chữ nhật
-
D.
$DE \bot DI$ (với $I$ là trung điểm $BH$)
Cho đường tròn tâm \(O\) bán kính \(6cm\) và một điểm \(A\) cách \(O\) là \(10cm\). Kẻ tiếp tuyến \(AB\) với đường tròn ( \(B\) là tiếp điểm). Tính độ dài \(AB\).
-
A.
\(AB = \,12\,cm\)
-
B.
\(AB = \,4\,cm\)
-
C.
\(AB = \,6\,cm\)
-
D.
\(AB = \,8\,cm\)
Cho đường tròn \((O).\) Từ một điểm \(M\) ở ngoài \((O)\), vẽ hai tiếp tuyến \(MA\) và \(MB\) sao cho góc \(AMB\) bằng \({60^0}\). Biết chu vi tam giác \(MAB\) là \(24\,cm\), tính độ dài bán kính đường tròn.
-
A.
\(8\,cm\)
-
B.
\(\,8\sqrt 3\,cm\)
-
C.
\(\dfrac {8}{\sqrt 3}\,cm\)
-
D.
\(5\,cm\)
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai ?
-
A.
$AC = CB$
-
B.
$\widehat {CBO'} = 90^\circ $
-
C.
$CA,CB$ là hai tiếp tuyến của $\left( {O'} \right)$
-
D.
$CA,CB$ là hai cát tuyến của $\left( {O'} \right)$
Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\)tiếp xúc ngoài tại \(A\). Kẻ các đường kính \(AOB;AO'C\). Gọi \(DE\) là tiếp tuyến chung của hai đường tròn \(\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)\). Gọi \(M\) là giao điểm của \(BD\) và \(CE\). Tính diện tích tứ giác \(ADME\) biết \(\widehat {DOA} = 60^\circ \) và \(OA = 8\,cm\)
-
A.
\(12\sqrt 3 \,\,c{m^2}\)
-
B.
\( \dfrac{64}{3}\sqrt 3 \,\,c{m^2}\)
-
C.
\( \dfrac{32}{3}\sqrt 3 \,\,c{m^2}\)
-
D.
\(36\,\,c{m^2}\)
Cho hai đường tròn $\left( {O;5} \right)$ và $\left( {O';5} \right)$ cắt nhau tại $A$ và $B.$ Biết $OO' = 8.$ Độ dài dây cung $AB$ là
-
A.
$6cm\;$
-
B.
$7cm$
-
C.
$5cm$
-
D.
$8cm$
Cho đường tròn \(\left( {O;R} \right)\). Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF đến đường tròn (với E, F là các tiếp điểm). Đoạn OM cắt đường tròn \(\left( {O;R} \right)\) tại I. Kẻ đường kính ED của \(\left( {O;R} \right)\). Hạ FK vuông góc với ED. Gọi P là giao điểm của MD và FK.
Chọn câu đúng.
-
A.
Các điểm M, E, O, F cùng thuộc một đường tròn.
-
B.
Điểm I là tâm đường tròn nội tiếp tam giác MEF.
-
C.
Điểm I là tâm đường tròn ngoại tiếp tam giác MEF.
-
D.
Cả A, B đều đúng
Cho \(FK = 4cm.\) Khi đó:
-
A.
\(FP = PK = 2cm\)
-
B.
\(P\) là trọng tâm tam giác \(FDE\)
-
C.
A, B đều đúng
-
D.
A, B đều sai
Cho \(\widehat {xOy}\) , trên Ox lấy P, trên Oy lấy Q sao cho chu vi ∆POQ bằng 2a không đổi. Chọn câu đúng.
-
A.
\(PQ\) luôn tiếp xúc với một đường tròn cố định
-
B.
\(PQ\) không tiếp xúc với một đường tròn cố định nào
-
C.
\(PQ = a\)
-
D.
\(PQ = OP\)
Lời giải và đáp án
Cho đường tròn \(\left( O \right)\)có hai dây \(AB,CD\) không đi qua tâm. Biết rằng khoảng cách từ tâm \(O\) đến dây \(AB\) lớn hơn khoảng cách từ tâm \(O\) đến dây \(CD\). Kết luận nào sau đây là đúng?
-
A.
\(AB > CD\)
-
B.
\(AB = CD\)
-
C.
\(AB < CD\)
-
D.
\(AB{\rm{//}}CD\)
Đáp án : C
- Trong một đường tròn: Dây nào gần tâm hơn thì dây đó lớn hơn.
Từ đề bài ta thấy dây \(CD\) gần tâm hơn dây \(AB\) nên \(CD > AB.\)
Cho \(\left( {O;4cm} \right)\). Đường thẳng \(d\) là tiếp tuyến của đường tròn \(\left( {O;4\,cm} \right)\), khi đó
-
A.
Khoảng cách từ \(O\) đến đường thẳng \(d\) nhỏ hơn \(4\,cm\)
-
B.
Khoảng cách từ \(O\) đến đường thẳng \(d\) bằng \(4\,cm\)
-
C.
Khoảng cách từ \(O\) đến đường thẳng \(d\) lớn hơn \(4\,cm\)
-
D.
Khoảng cách từ \(O\) đến đường thẳng \(d\) bằng \(5\,cm\)
Đáp án : B
Khoảng cách từ tâm của một đường tròn đến tiếp tuyến bằng bán kính của đường tròn đó.
Cho đường tròn $\left( O \right)$ có bán kính $R = 5\,cm$. Khoảng cách từ tâm đến dây $AB$ là $3\,cm$. Tính độ dài dây $AB$.
-
A.
$AB = 6\,cm$
-
B.
$AB = 8\,cm$
-
C.
$AB = 10\,cm$
-
D.
$AB = 12\,cm$
Đáp án : B
Sử dụng kiến thức “Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy”, sau đó dùng định lý Pytago vào tam giác vuông thích hợp.
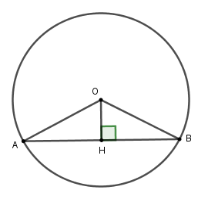
Kẻ $OH \bot AB$ tại $H$ suy ra $H$ là trung điểm của $AB$.
Xét tam giác $OHB$ vuông tại $H$ có $OH = 3;OB = 5$. Theo định lý Pytago ta có $HB = \sqrt {O{B^2} - O{H^2}} = \sqrt {{5^2} - {3^2}} = 4$
Mà $H$ là trung điểm của $AB$ nên $AB = 2HB = 8\,cm$
Vậy $AB = 8\,cm$.
Cho đường tròn \(\left( O \right)\) và điểm \(A\) nằm trên đường tròn \(\left( O \right).\) Nếu đường thẳng \(d \bot OA\) tại \(A\) thì
-
A.
\(d\) là tiếp tuyến của \(\left( O \right)\)
-
B.
\(d\) cắt \(\left( O \right)\) tại hai điểm phân biệt
-
C.
\(d\) là tiếp xúc với \(\left( O \right)\) tại \(O\)
-
D.
Cả A, B, C đều sai
Đáp án : A
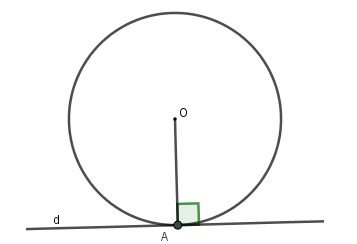
Nếu một đường thẳng đi qua một điểm thuộc đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng đó là tiếp tuyến của đường tròn.
Hay \(d\) là tiếp tuyến của \(\left( O \right)\) tại \(A.\)
Đường tròn là hình:
-
A.
Không có trục đối xứng
-
B.
Có một trục đối xứng
-
C.
Có hai trục đối xứng
-
D.
Có vô số trục đối xứng
Đáp án : D
Hình có trục đối xứng là hình khi lấy đối xứng hình đó qua trục đối xứng ta cũng được chính hình đó.
Đường tròn có trục đối xứng là đường thẳng đi qua tâm của nó. Do có vô số đường kính nên đường tròn có vô số trục đối xứng.
Trong hình vẽ bên cho $OC \bot AB,AB = 12cm,OA = 10cm$. Độ dài $AC$ là:

-
A.
$8cm$
-
B.
$2\sqrt {10} cm$
-
C.
$4\sqrt 7 cm$
-
D.
$2cm$
Đáp án : B
Dựa vào tính chất bán kính vuông góc với dây cung.
Dựa vào định lí Pi-ta-go trong tam giác vuông.
Vì $OC$ vuông góc với $AB$ nên $D$ là trung điểm của $AB$ (mối quan hệ giữa đường kính và dây)
$ \Rightarrow AD = \dfrac{{AB}}{2} = \dfrac{{12}}{2} = 6cm$.
Xét tam giác $AOD$ vuông tại $D$ nên $O{D^2} = O{A^2} - A{D^2} = {10^2} - {6^2} = 64 \Rightarrow OD = 8cm$.
Có $OD + DC = OC$ nên $DC = OC - OD = 10 - 8 = 2cm$.
Xét tam giác $ADC$ vuông tại $D$ nên $A{C^2} = A{D^2} + D{C^2} = {6^2} + {2^2} = 40$ .
Vậy $AC = 2\sqrt {10} cm$.
Cho đường tròn $\left( {O;3cm} \right)$, lấy điểm $A$ sao cho $OA = 6cm$. Từ \(A\) vẽ tiếp tuyến $AB,AC$ đến đường tròn $\left( O \right)$ ($B,C$ là tiếp điểm). Chu vi tam giác $ABC$ là
-
A.
$9cm$
-
B.
$9\sqrt 3 cm$
-
C.
$9\sqrt 2 cm$
-
D.
Kết quả khác
Đáp án : B
Dựa vào tính chất tiếp tuyến của đường tròn
Định lí Pi-ta-go
Hệ thức lượng trong tam giác vuông
Cách tính chu vi hình tam giác
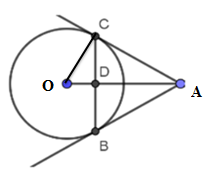
Gọi $D$ là giao điểm của $BC$ và $OA$
Có $OC \bot AC$ (tính chất tiếp tuyến của đường tròn)
Xét $\Delta OAC$ vuông tại \(C\), ta có: $O{C^2} + C{A^2} = O{A^2}$ (Py-ta-go)
\( \Rightarrow A{C^2} = {\rm{ }}O{A^2} - {\rm{ }}O{C^2} = {6^2} - {3^2} = 36 - 9 = 27 \Rightarrow AC = 3\sqrt 3 cm\)
Mà $AC=AB$ (tính chất hai tiếp tuyến cắt nhau) nên $AB = 3\sqrt 3 cm$.
Vì $AC=AB;OB=OC$ nên $OA$ là đường trung trực của $BC$ hay $OA \bot BC$ tại $D$ và $D$ là trung điểm của $CB.$
Xét tam giác vuông $OCA$ có $CD$ là đường cao nên:
\(CD = \dfrac{{OC.CA}}{{OA}} = \dfrac{{3.3\sqrt 3 }}{6} = \dfrac{{3\sqrt 3 }}{2} \Rightarrow BC = 2CD = 3\sqrt 3 cm\)
Vậy chu vi tam giác $ABC$ là $3\sqrt 3 + 3\sqrt 3 + 3\sqrt 3 = 9\sqrt 3 cm$
Từ một điểm $A$ ở bên ngoài đường tròn $\left( {O;R} \right)$,vẽ hai tiếp tuyến $AB,AC$ với $\left( O \right)$. Đường thẳng vuông góc với $OB$ tại $O$ cắt tia $AC$ tại $N$. Đường thẳng vuông góc với $OC$ tại $O$ cắt tia $AB$ tại $M$.
Điểm $A$ phải cách $O$ một khoảng là bao nhiêu để cho $MN$ là tiếp tuyến của $\left( O \right)$?
-
A.
$OA = 2R$
-
B.
$OA = \dfrac{3}{2}R$
-
C.
$OA = 3R$
-
D.
$OA = \dfrac{4}{3}R$
Đáp án: A
Sử dụng tính chất của hình thoi.
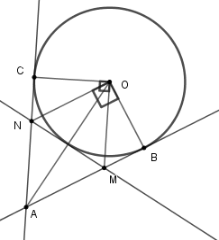
Tứ giác $AMON$ là hình thoi nên \(OA \bot MN\) và
Mà độ dài $OA$ bằng $2$ lần khoảng cách từ $O$ đến $MN$ .
Do đó $MN$ là tiếp tuyến đường tròn \(\left( {O;{\rm{ R}}} \right) \) suy ra khoảng cách từ $O$ đến $MN$ bằng R hay \( OA = 2R\).
T ứ giác $AMON$ là hình gì?
-
A.
H ình bình hành
-
B.
H ình thoi
-
C.
H ình thang
-
D.
H ình chữ nhật
Đáp án: B
Sử dụng dấu hiệu nhận biết các hình đặc biệt.
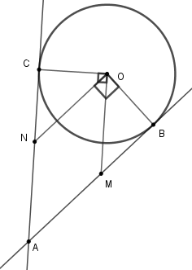
Dễ có $AMON$ là hình bình hành (Vì $ON{\rm{//}}AM;OM{\rm{//}}AN$).
Ta chứng minh \(OM = ON\).
Xét tam giác $OBM$ và tam giác $OCN$ có :
\(\widehat {OBM} = \widehat {OCN} = {90^0};\)
\({\rm{ }}OB = OC = R,\)
và \(\widehat {OMB} = \widehat {ONC} = \widehat A \)
\(\Rightarrow \Delta OBM = \Delta OCN\)
\( \Rightarrow OM = ON \Rightarrow AMON\) là hình thoi .
Cho nửa đường tròn tâm $O$ đường kính $AB.$ Vẽ các tiếp tuyến $Ax$ và $By$ ($Ax$ và $By$ và nửa đường tròn cùng thuộc về một nửa mặt phẳng bờ là $AB$ ). Gọi $M$ là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại $M$ cắt $Ax$ và $By$ theo thứ tự tại $C$ và $D.$ Lấy $I$ là trung điểm của $CD.$
Chọn câu sai.
-
A.
Đường tròn có đường kính $CD$ tiếp xúc với $AB.$
-
B.
Đường tròn có đường kính $CD$ cắt $AB.$
-
C.
$IO\; \bot AB$
-
D.
\(IO = \dfrac{{DC}}{2}\)
Đáp án: B
Sử dụng tính chất hai tiếp tuyến cắt nhau và tính chất đường trung bình của hình thang
Sử dụng vị trí tương đối của hai đường tròn
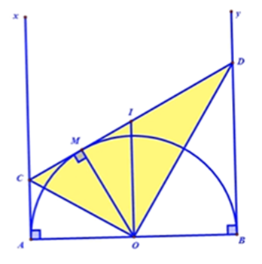
Vì \(I\) là trung điểm của \(CD.\)
Nên \(I\) là tâm của đường tròn đường kính \(CD.\)
Theo tính chất hai tiếp tuyến cắt nhau: $AC = CM\;$ và $BD = DM$
Xét tứ giác $ABDC$ có: $AC//BD \Rightarrow ABDC$ là hình thang
Suy ra $IO$ là đường trung bình của hình thang $ABDC$
\( \Rightarrow \) $IO//AC//BD$ mà $AC\; \bot AB \Rightarrow IO\; \bot AB{\rm{ }}\left( 1 \right)$
$IO = \dfrac{{AC + BD}}{2} = \dfrac{{CM + DM}}{2} = \dfrac{{CD}}{2}(2)$
Từ (1) và (2) suy ra đường tròn đường kính $CD$ tiếp xúc với $AB.$
Vậy A,C,D đúng, B sai.
Hình thang $ABDC$ có chu vi nhỏ nhất là
-
A.
\(AB\)
-
B.
\(2AB\)
-
C.
\(3AB\)
-
D.
\(4AB\)
Đáp án: C
Sử dụng tính chất hai tiếp tuyến cắt nhau
Sử dụng công thức tính chu vi hình thang và lập luận để có chu vi nhỏ nhất
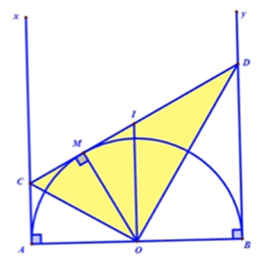
Theo tính chất hai tiếp tuyến cắt nhau: $AC = CM\;$ và $BD = DM$
Chu vi hình thang $ABDC$ là:
${P_{ABDC}} = AC + AB + BD + CD $$= CM + AB + DM + CD = AB + 2CD$
$ \Rightarrow {P_{ABDC}}_{\min }\,{\rm{khi}}\,\,C{D_{\min }} \Rightarrow CD = AB \Rightarrow CD//AB$
Mà $OM\; \bot CD{\rm{ }} \Rightarrow OM\; \bot AB$
$ \Rightarrow {P_{ABDC\min }} = AB + 2AB = 3AB$
Vậy chu vi nhỏ nhất của hình thang $ABDC$ là $3AB$ khi $OM$ $ \bot $ $AB$ .
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Đường tròn đường kính $BH$ cắt $AB$ tại $D$, đường tròn đường kính $CH$ cắt $AC$ tại $E$ . Chọn khẳng định sai trong các khẳng định sau
-
A.
$DE$ là cát tuyến của đường tròn đường kính $BH$
-
B.
$DE$ là tiếp tuyến của đường tròn đường kính $BH$
-
C.
Tứ giác$AEHD$ là hình chữ nhật
-
D.
$DE \bot DI$ (với $I$ là trung điểm $BH$)
Đáp án : A
Sử dụng dấu hiệu nhận biết các hình đặc biệt và cách chứng minh một đường thẳng là tiếp tuyến của đường tròn.
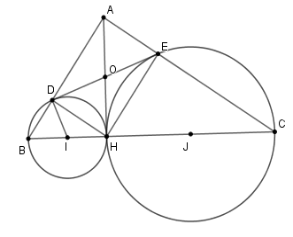
Gọi $I$, $J$ lần lượt là trung điểm của $BH$ và $CH.$
Để chứng minh $DE$ là tiếp tuyến của đường tròn tâm $I$ đường kính $BH$ ta chứng minh
\(ID \bot DE\) hay $\widehat {ODI} = {90^o}$
Vì $D,E$ lần lượt thuộc đường tròn đường kính $BH$ và $HC$ nên ta có: $\widehat {BDH} = \widehat {CEH} = {90^0}$
Suy ra tứ giác $ADHE$ là hình chữ nhật.
Gọi $O$ là giao điểm của $AH$ và$DE$, khi đó ta có $OD = OH = OE = OA$ .
Suy ra $\Delta ODH$ cân tại $O \Rightarrow \widehat {ODH} = \widehat {OHD}$
Ta cũng có $\Delta IDH$ cân tại $I$$ \Rightarrow \widehat {IDH} = \widehat {IHD}$
Từ đó $ \Rightarrow \widehat {IDH} + \widehat {HDO} = \widehat {IHD} + \widehat {DHO} \Rightarrow \widehat {IDO} = 90^\circ $$ \Rightarrow ID \bot DE$
Ta có \(ID \bot DE,D \in \left( I \right)\) nên $DE$ là tiếp tuyến của đường tròn đường kính $BH$.
Từ chứng minh trên suy ra các phương án B,C,D đúng.
Cho đường tròn tâm \(O\) bán kính \(6cm\) và một điểm \(A\) cách \(O\) là \(10cm\). Kẻ tiếp tuyến \(AB\) với đường tròn ( \(B\) là tiếp điểm). Tính độ dài \(AB\).
-
A.
\(AB = \,12\,cm\)
-
B.
\(AB = \,4\,cm\)
-
C.
\(AB = \,6\,cm\)
-
D.
\(AB = \,8\,cm\)
Đáp án : D
Sử dụng định lý về tiếp tuyến của đường tròn và định lý Pytago để tính toán
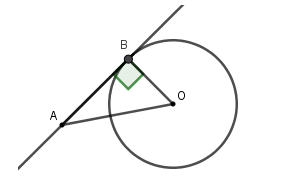
Vì \(AB\) là tiếp tuyến và \(B\) là tiếp điểm nên \(OB = R = 6\,cm\); \(AB \bot OB\) tại \(B\).
Áp dụng định lý Pytago cho tam giác \(ABO\) vuông tại \(B\) ta được \(AB = \sqrt {O{A^2} - O{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\,cm\)
Vậy \(AB = \,8\,cm\).
Cho đường tròn \((O).\) Từ một điểm \(M\) ở ngoài \((O)\), vẽ hai tiếp tuyến \(MA\) và \(MB\) sao cho góc \(AMB\) bằng \({60^0}\). Biết chu vi tam giác \(MAB\) là \(24\,cm\), tính độ dài bán kính đường tròn.
-
A.
\(8\,cm\)
-
B.
\(\,8\sqrt 3\,cm\)
-
C.
\(\dfrac {8}{\sqrt 3}\,cm\)
-
D.
\(5\,cm\)
Đáp án : C
Sử dụng tính chất hai tiếp tuyến cắt nhau và công thức chu vi tam giác
Sử dụng tỉ số lượng giác của góc nhọn
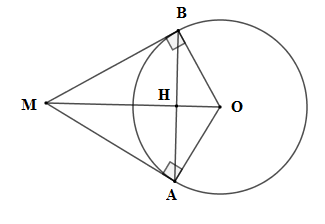
Xét \(\left( O \right)\) có \(MA = MB\) (tính chất hai tiếp tuyến cắt nhau) mà \(\widehat {AMB} = 60^\circ \) nên \(\Delta MAB\) đều suy ra chu vi \(\Delta MAB\) là \(MA + MB + AB = 3AB = 24 \)\(\Rightarrow AB = 8cm = MA = MB\)
Lại có \(\widehat {AMO} = \dfrac{1}{2}\widehat {AMB} = 30^\circ \) (tính chất 2 tiếp tuyến cắt nhau)
Xét tam giác vuông \(MAO\) có \(\tan \widehat {AMO} = \dfrac{{OA}}{{MA}} \Rightarrow OA = MA.\tan 30^\circ = \dfrac {8}{\sqrt 3}\,cm\)
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai ?
-
A.
$AC = CB$
-
B.
$\widehat {CBO'} = 90^\circ $
-
C.
$CA,CB$ là hai tiếp tuyến của $\left( {O'} \right)$
-
D.
$CA,CB$ là hai cát tuyến của $\left( {O'} \right)$
Đáp án : D
Sử dụng cách chứng minh một đường thẳng là tiếp tuyến của đường tròn.
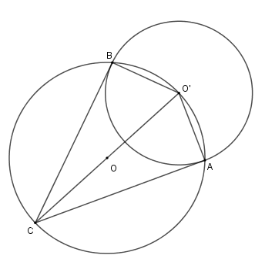
Xét đường tròn $\left( O \right)$ có $O'C$ là đường kính, suy ra $\widehat {CBO'} = \widehat {CAO'} = 90^\circ $ hay $CB \bot O'B$ tại $B$ và $AC \bot AO'$ tại $A$.
Do đó $AB,BC$ là hai tiếp tuyến của $\left( {O'} \right)$ nên $AC = CB$ (tính chất hai tiếp tuyến cắt nhau)
Nên A, B, C đúng.
Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\)tiếp xúc ngoài tại \(A\). Kẻ các đường kính \(AOB;AO'C\). Gọi \(DE\) là tiếp tuyến chung của hai đường tròn \(\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)\). Gọi \(M\) là giao điểm của \(BD\) và \(CE\). Tính diện tích tứ giác \(ADME\) biết \(\widehat {DOA} = 60^\circ \) và \(OA = 8\,cm\)
-
A.
\(12\sqrt 3 \,\,c{m^2}\)
-
B.
\( \dfrac{64}{3}\sqrt 3 \,\,c{m^2}\)
-
C.
\( \dfrac{32}{3}\sqrt 3 \,\,c{m^2}\)
-
D.
\(36\,\,c{m^2}\)
Đáp án : B
Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và hệ thức lượng trong tam giác vuông.
Diện tích hình chữ nhật bằng tích chiều dài và chiều rộng.
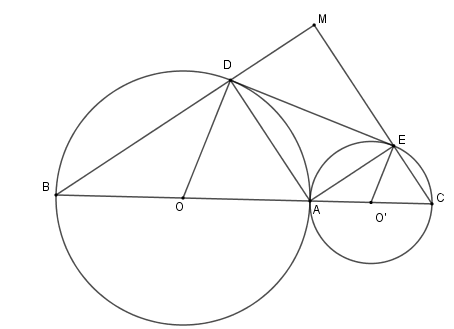
Xét \(\left( O \right)\) có \(OD = OA \Rightarrow \Delta OAD\) cân tại \(O \Rightarrow \widehat {ODA} = \widehat {OAD}\)
Xét \(\left( {O'} \right)\) có \(O'E = O'A \Rightarrow \Delta O'EB\) cân tại \(O' \Rightarrow \widehat {O'EA} = \widehat {O'AE}\)
Mà \(\widehat O + \widehat {O'} = 360^\circ - \widehat {O'ED} - \widehat {ODE} = 180^\circ \)
\( \Leftrightarrow 180^\circ - \widehat {ODA} - \widehat {OAD} + 180^\circ - \widehat {O'EA} - \widehat {O'AE} = 180^\circ \Leftrightarrow 2\left( {\widehat {OAD} + \widehat {O'AE}} \right) = 180^\circ \)
\( \Rightarrow \widehat {OAD} + \widehat {O'AE} = 90^\circ \)\( \Rightarrow \widehat {DAE} = 90^\circ \Rightarrow \Delta ADE\) vuông tại \(A\).
Mà \(\widehat {BDA} = 90^\circ \) ( vì tam giác \(BAD\) có cạnh \(AB\) là đường kính của \(\left( O \right)\)và \(D \in \left( O \right)\) ) nên \(BD \bot AD \Rightarrow \widehat {MDA} = 90^\circ \)
Tương tự ta có \(\widehat {MEA} = 90^\circ \) .\(\)\(\)
Nên tứ giác \(DMEA\) là hình chữ nhật.
Xét tam giác \(OAD\) cân tại \(O\) có \(\widehat {DOA} = 60^\circ \) nên \(\Delta DOA\) đều, suy ra \(OA = AD = 8\,cm\) và \(\widehat {ODA} = 60^\circ \)
\( \Rightarrow \widehat {ADE} = 30^\circ \). Xét tam giác \(ADE\) ta có \(EA = AD.\tan \widehat {EDA} = 8.\tan 30^\circ = \dfrac{8}{3}\sqrt 3 \)
\({S_{DMEA}} = AD.AE = 8.\dfrac{8}{3}\sqrt 3 = \dfrac{64}{3}\sqrt 3 \,\,c{m^2}\).
Cho hai đường tròn $\left( {O;5} \right)$ và $\left( {O';5} \right)$ cắt nhau tại $A$ và $B.$ Biết $OO' = 8.$ Độ dài dây cung $AB$ là
-
A.
$6cm\;$
-
B.
$7cm$
-
C.
$5cm$
-
D.
$8cm$
Đáp án : A
Tính chất tam giác cân
Đinh lí pi-ta-go
Tính chất hai đường tròn cắt nhau
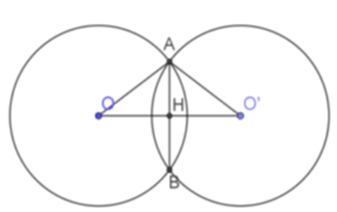
Ta có $OA = O'A = 5cm$ nên tam giác $AOO'$ cân tại A.
Mà AH vuông góc với OO’ nên H là trung điểm của OO’. Suy ra $OH = 4cm$ .
Xét tam giác AOH vuông tại H nên suy ra
$A{H^2} = O{A^2} - O{H^2} = {5^2} - {4^2} = 9 = {3^2}$.
Vậy $AH = 3cm$ .
Mà $AB = 2AH$ ( mối quan hệ giữa đường nối tâm và dây cung).
Vậy $AB = 6cm$
Cho đường tròn \(\left( {O;R} \right)\). Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF đến đường tròn (với E, F là các tiếp điểm). Đoạn OM cắt đường tròn \(\left( {O;R} \right)\) tại I. Kẻ đường kính ED của \(\left( {O;R} \right)\). Hạ FK vuông góc với ED. Gọi P là giao điểm của MD và FK.
Chọn câu đúng.
-
A.
Các điểm M, E, O, F cùng thuộc một đường tròn.
-
B.
Điểm I là tâm đường tròn nội tiếp tam giác MEF.
-
C.
Điểm I là tâm đường tròn ngoại tiếp tam giác MEF.
-
D.
Cả A, B đều đúng
Đáp án: D
+ Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền
+ Tâm đường tròn nội tiếp tam giác là giao ba đường phân giác
+ Tâm đường tròn ngoại tiếp tam giác là giao ba đường trung trực
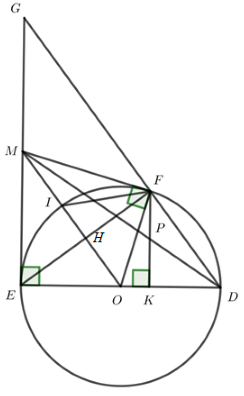
* Vì ME là tiếp tuyến của \(\left( O \right)\) nên ME vuông góc với OE, suy ra tam giác MOE nội tiếp đường tròn đường kính MO (1)
Vì MF là tiếp tuyến của \(\left( O \right)\) nên MF vuông góc với OF, suy ra tam giác MOF nội tiếp đường tròn đường kính MO (2)
Từ (1) và (2) suy ra M, E, O, F cùng thuộc một đường tròn nên A đúng.
* Gọi \(MO \cap EF = \left\{ H \right\}\)
Vì M là giao điểm của 2 tiếp tuyến ME và MF của \(\left( O \right)\)
\( \Rightarrow ME = MF\) (tính chất) mà \(OE = OF = R\) (gt)
\( \Rightarrow \) MO là đường trung trực của EF
\( \Rightarrow MO \bot EF\)
\( \Rightarrow \angle IFE + \angle OIF = {90^o}\,\)
Vì \(OI = OF = R\) nên tam giác OIF cân tại O
\( \Rightarrow \angle OIF = \angle OFI\) mà \(\angle MFI + \angle OFI = {90^o}\,;\,\,\,\angle IFE + \angle OIF = {90^o}\)
\( \Rightarrow \angle MFI = \angle IFE\)
\( \Rightarrow \) FI là phân giác của \(\angle MFE\) (1)
Vì M là giao điểm của 2 tiếp tuyến ME và MF của \(\left( O \right)\)
\( \Rightarrow \) MI là phân giác của \(\angle EMF\) (tính chất) (2)
Từ (1) và (2) \( \Rightarrow \) I là tâm đường tròn nội tiếp tam giác MEF
Cho \(FK = 4cm.\) Khi đó:
-
A.
\(FP = PK = 2cm\)
-
B.
\(P\) là trọng tâm tam giác \(FDE\)
-
C.
A, B đều đúng
-
D.
A, B đều sai
Đáp án: A
Kéo dài DF và EM cắt nhau tại G từ đó sử dụng định lý Ta-let để chứng minh.
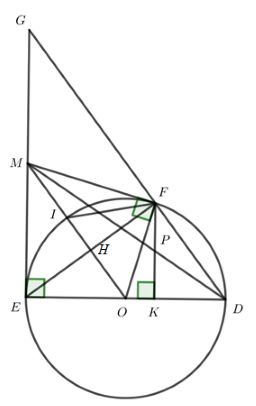
Gọi G là giao điểm của tia DF và tia EM.
Ta có \(\angle EFD = {90^o}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow EF \bot DG\) mà \(EF \bot OM\) (cmt)
\( \Rightarrow OM//DG\) (từ vuông góc đến song song)
Tam giác EDG có \(OE = OD\,\,;\,\,OM//DG\,\, \Rightarrow ME = MG\)(tính chất đường trung bình)
Áp dụng định lý Ta-let cho tam giác EDM có \(PK//ME\) (cùng vuông góc với ED) ta được: \(\dfrac{{PK}}{{ME}} = \dfrac{{DP}}{{DM}}\) (3)
Áp dụng định lý Ta-let cho tam giác MDG có \(PF//MG\) (cùng vuông góc với ED) ta được: \(\dfrac{{PF}}{{MG}} = \dfrac{{DP}}{{DM}}\) (4)
Từ (3) và (4) suy ra \(\dfrac{{PK}}{{ME}} = \dfrac{{PF}}{{MG}}\) mà \(ME = MG\) (cmt)
\( \Rightarrow PK = PF\,\, \Rightarrow \) P là trung điểm của FK. Suy ra \(FP = PK = \dfrac{4}{2} = 2cm\)
Cho \(\widehat {xOy}\) , trên Ox lấy P, trên Oy lấy Q sao cho chu vi ∆POQ bằng 2a không đổi. Chọn câu đúng.
-
A.
\(PQ\) luôn tiếp xúc với một đường tròn cố định
-
B.
\(PQ\) không tiếp xúc với một đường tròn cố định nào
-
C.
\(PQ = a\)
-
D.
\(PQ = OP\)
Đáp án : A
Sử dụng tính chất tia phân giác, hai tam giác bằng nhau
Và điều kiện tiếp xúc của đường thẳng với đường tròn.
Đường thẳng \(d\) tiếp xúc với đường tròn \(\left( O \right)\) tại \(M\) khi \(M \in \left( O \right)\) và \(OM = R.\)
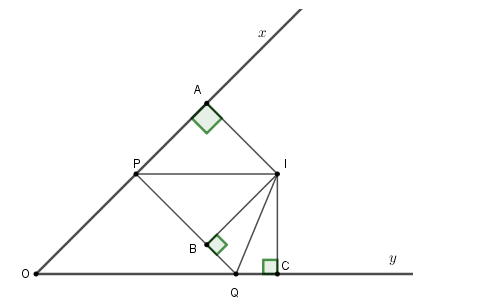
Gọi I là giao điểm các tia phân giác của \(\widehat {xPQ};\,\widehat {yQP}\) và A, B, C lần lượt là hình chiếu của I lên Ox, PQ và Oy.
Vì I thuộc phân giác của góc xPQ nên IA = IB.
Xét ∆PAI và ∆PBI có :
+ IA = IB (cmt)
+ Chung PI
+ \(\widehat {PAI} = \widehat {PBI} = 90^\circ \)
nên ∆PAI = ∆PBI (cạnh huyền – cạnh góc vuông) ,
Suy ra PA = PB.
Lí luận tương tự, ta có \(QB = QC.\)
\(OA + OC = OP + PA + OQ + QC\) \( = OP + PB + OQ + QB = OP + PQ + QO = 2a\) (do chu vi ∆OPQ bằng 2a).
Vì IA = IB và IB = IC (cmt) nên IA = IC.
Xét ∆OAI và ∆OCI có
+ IA = IC (cmt)
+ \(\widehat {OAI} = \widehat {OCI} = 90^\circ \)
+ cạnh chung OI
nên ∆OAI = ∆OCI (cạnh huyền – cạnh góc vuông) \( \Rightarrow OA = OC = \dfrac{{2a}}{2} = a{\rm{ }}.\)
Vì a không đổi và A, C thuộc tia Ox, Oy cố định nên A và C cố định.
Do A và C lần lượt là hình chiếu của I lên Ox, Oy nên hai đường thẳng AI và CI cố định hay I cố định.
Do I và A cố định nên độ dài đoạn thẳng AI không đổi.
Do IA = IB (cmt) nên IB là bán kính của đường tròn (I ; IA), mà IB ⊥ PQ tại B nên PQ tiếp xúc với đường tròn (I; IA) cố định.