Đề kiểm tra giữa học kì 1 Toán 9 - Đề số 1
Đề bài
Cho $\alpha $ và $\beta $ là hai góc nhọn bất kỳ thỏa mãn $\alpha + \beta = 90^\circ $. Khẳng định nào sau đây là đúng ?
-
A.
$\tan \alpha = \sin \beta $
-
B.
$\tan \alpha = \cot \beta $
-
C.
$\tan \alpha = \cos \alpha $
-
D.
$\tan \alpha = \tan \beta $
Cho số thực \(a > 0\). Căn bậc hai số học của \(a\) là \(x\) khi và chỉ khi
-
A.
\(x = \sqrt a \)
-
B.
\(\sqrt x = a\)
-
C.
\({a^2} = x\,\) và \(x \ge 0\)
-
D.
\({x^2} = a\,\) và \(x \ge 0\)
Khẳng định nào sau đây là đúng?
-
A.
$\sqrt[3]{a} = x$ nếu x = ${a^3}$
-
B.
$\sqrt[3]{a} = - x $ nếu $ - x= {a^3} $
-
C.
$\sqrt[3]{a} = x $ nếu ${x^3} = a$
-
D.
$\sqrt[3]{a} = - x$ nếu ${x^3} = a$
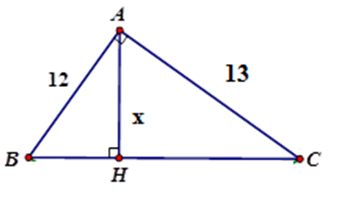
Tính $x$ trong hình vẽ sau (làm tròn đến chữ số thập phân thứ hai)
-
A.
$x \approx 8,81$
-
B.
$x \approx 8,82$
-
C.
$x \approx 8,83$
-
D.
$x \approx 8,80$
Kết quả của phép tính $\sqrt {\dfrac{{81}}{{169}}} $ là?
-
A.
$\dfrac{9}{{13}}$
-
B.
$\dfrac{9}{{169}}$
-
C.
$\dfrac{3}{{13}}$
-
D.
$\dfrac{{13}}{9}$
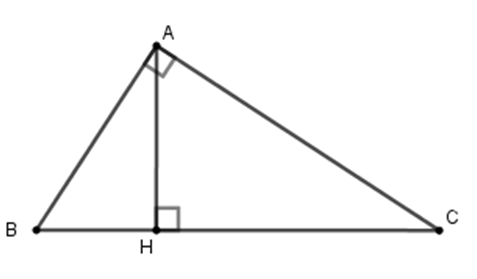
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là đúng ?
-
A.
$A{H^2} = AB.AC$
-
B.
$A{H^2} = BH.CH$
-
C.
$A{H^2} = AB.BH$
-
D.
$A{H^2} = CH.BC$
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 9\,cm,\,\,AC = 5cm.\) Tính tỉ số lượng giác \(\tan C\) (làm tròn đến chữ số thập phân thứ \(1\) )
-
A.
\(\tan C \approx 0,67\)
-
B.
\(\tan C \approx 0,5\)
-
C.
\(\tan C \approx 1,4\)
-
D.
\(\tan C \approx 1,5\)
Một cầu trượt trong công viên có độ dốc là ${28^0}$ và có độ cao là $2,1m.$Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ hai).
-
A.
$3,95\,m$
-
B.
$3,8\,m$
-
C.
$4,5\,m$
-
D.
$4,47\,m$
So sánh hai số \(5\) và \(\sqrt {50} - 2\).
-
A.
\(5 > \sqrt {50} - 2\)
-
B.
\(5 = \sqrt {50} - 2\)
-
C.
\(5 < \sqrt {50} - 2\)
-
D.
Chưa đủ điều kiện để so sánh.
Đưa thừa số $5y\sqrt y $ ($y \ge 0$) vào trong dấu căn ta được
-
A.
$\sqrt {5{y^2}} $
-
B.
$\sqrt {25{y^3}} $
-
C.
$\sqrt {5{y^3}} $
-
D.
$\sqrt {25y\sqrt y } $
Phép tính $\sqrt {{{\left( { - 5} \right)}^2}{{.7}^2}} $ có kết quả là?
-
A.
$35$
-
B.
$5$
-
C.
$ - 35$
-
D.
Không tồn tại.
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.
-
A.
$\sin \alpha + \cos \alpha = 1$
-
B.
${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
-
C.
${\sin ^3}\alpha + {\cos ^3}\alpha = 1$
-
D.
$\sin \alpha - cos\alpha = 1$
Cho $a$ là số không âm, $b$ là số dương. Khẳng định nào sau đây là đúng?
-
A.
$\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{b}$
-
B.
$\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}$
-
C.
$\sqrt {\dfrac{a}{b}}=\dfrac{{ - \sqrt a }}{{\sqrt b }}$
-
D.
$\sqrt {\dfrac{a}{b}}=\dfrac{a}{{\sqrt b }}$
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 15\,cm,\widehat B = 55^\circ .\) Tính \(AC;\widehat C\) . (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(AC \approx 12,29;\widehat C = 45^\circ \)
-
B.
\(AC \approx 12,29;\widehat C = 35^\circ \)
-
C.
\(AC \approx 12,2;\widehat C = 35^\circ \)
-
D.
\(AC \approx 12,92;\widehat C = 40^\circ \)
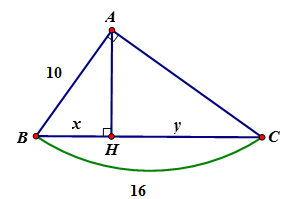
Tính \(x,y\) trong hình vẽ sau:
-
A.
\(x = 6,5;y = 9,5\)
-
B.
\(x = 6,25;y = 9,75\)
-
C.
\(x = 9,25;y = 6,75\)
-
D.
\(x = 6;y = 10\)
Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 1\,cm,\,\,BC = 2\,cm.\) Tính các tỉ số lượng giác \(\sin B;\cos B\)
-
A.
\(\sin B = \dfrac{1}{{\sqrt 3 }};\cos B = \dfrac{{2\sqrt 3 }}{3}\)
-
B.
\(\sin B = \dfrac{{\sqrt 5 }}{5};\cos B = \dfrac{{2\sqrt 5 }}{5}\)
-
C.
\(\sin B = \dfrac{1}{2};\cos B = \dfrac{2}{{\sqrt 5 }}\)
-
D.
\(\sin B = \dfrac{{2\sqrt 5 }}{5};\cos B = \dfrac{{\sqrt 5 }}{5}\)
Tính giá trị biểu thức \(\sqrt {19 + 8\sqrt 3 } + \sqrt {19 - 8\sqrt 3 } \).
-
A.
\(2\sqrt 3 \)
-
B.
\(8 + 2\sqrt 3 \)
-
C.
\(6\)
-
D.
\(8\)
Giá trị biểu thức \(\sqrt {5x + 3} .\sqrt {5x - 3} \) khi \(x = \sqrt {3,6} \) là:
-
A.
\(3,6\)
-
B.
\(3\)
-
C.
\(81\)
-
D.
\(9\)
Rút gọn biểu thức $4{a^4}{b^2}.\sqrt {\dfrac{9}{{{a^8}{b^4}}}} $ với $ab \ne 0$ ta được
-
A.
$\dfrac{{{a^2}}}{b}$
-
B.
$12$
-
C.
$6$
-
D.
$36$
Rút gọn biểu thức \(\dfrac{a}{{\sqrt 5 + 1}} + \dfrac{a}{{\sqrt 5 - 2}} - \dfrac{a}{{3 - \sqrt 5 }} - \sqrt 5 a\) ta được
-
A.
$2a$
-
B.
$a$
-
C.
$3a$
-
D.
$12a$
Rút gọn biểu thức \(5\sqrt a - 4b\sqrt {25{a^3}} + 5a\sqrt {16a{b^2}} - \sqrt {9a} \) với $a \ge 0;b \ge 0$ ta được kết quả là
-
A.
$2\sqrt {2a} $
-
B.
$4\sqrt a $
-
C.
$8\sqrt a $
-
D.
$2\sqrt a $
Cho $P = \dfrac{2}{{\sqrt x + 1}}$ .
Có bao nhiêu giá trị $x \in \mathbb{Z}$ để $P \in \mathbb{Z}$ ?
-
A.
$1$
-
B.
$2$
-
C.
$0$
-
D.
$4$
Rút gọn biểu thức \(2\sqrt a - \sqrt {9{a^3}} + {a^2}\sqrt {\dfrac{{16}}{a}} + \dfrac{2}{{{a^2}}}\sqrt {36{a^5}} \) với $a > 0$ ta được
-
A.
$14\sqrt a + a\sqrt a $
-
B.
$14\sqrt a - a\sqrt a $
-
C.
$14\sqrt a + 2a\sqrt a $
-
D.
$20\sqrt a - 2a\sqrt a $
Thu gọn biểu thức \(\dfrac{{\sqrt[3]{{ - 64{a^5}{b^5}}}}}{{\sqrt[3]{{{a^2}{b^2}}}}}\) ta được:
-
A.
\(4ab\)
-
B.
\( - 8ab\)
-
C.
\(16ab\)
-
D.
\( - 4ab\)
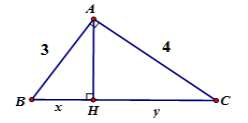
Tính \(x,y\) trong hình vẽ sau:
-
A.
\(x = 3,2;y = 1,8\)
-
B.
\(x = 1,8;y = 3,2\)
-
C.
\(x = 2;y = 3\)
-
D.
\(x = 3;y = 2\)
Tính $x,y$ trong hình vẽ sau:
-
A.
$x = \dfrac{{35\sqrt {74} }}{{74}};y = \sqrt {74} $
-
B.
$y = \dfrac{{35\sqrt {74} }}{{74}};x= \sqrt {74} $
-
C.
$x = 4;y = 6$
-
D.
$x = 2,8;y = 7,2$
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(AB = 13\,cm,\,BH = 0,5\,dm\) Tính tỉ số lượng giác $\sin C$ (làm tròn đến chữ số thập phân thứ $2$ )
-
A.
$\sin C \approx 0,35$
-
B.
$\sin C \approx 0,37$
-
C.
$\sin C \approx 0,39$
-
D.
$\sin C \approx 0,38$
Tính giá trị biểu thức \(B = \tan 10^\circ .\tan 20^\circ .\tan 30^\circ .....tan80^\circ \)
-
A.
\(B = 44\)
-
B.
\(B = 1\)
-
C.
\(B = 45\)
-
D.
\(B = 2\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 7\,cm,AB = \,5cm\). Tính $BC;\widehat C$ .
-
A.
$BC = \sqrt {74} (cm);\widehat C \approx 35^\circ 32'$
-
B.
$BC = \sqrt {74} (cm);\widehat C \approx 36^\circ 32'$
-
C.
$BC = \sqrt {74} (cm) ;\widehat C \approx 35^\circ 33'$
-
D.
$BC = \sqrt {75} (cm) ;\widehat C \approx 35^\circ 32'$
Cho tam giác \(ABC\) có \(AB = 16,AC = 14\) và \(\widehat B = {60^0}\). Tính $BC$
-
A.
$BC = 10$
-
B.
$BC = 11$
-
C.
$BC = 9$
-
D.
$BC = 12$
Một máy bay đang bay ở độ cao \(12km\) so với mặt đất, muốn hạ cánh xuống sân bay. Để đường bay và mặt đất hợp thành một góc an toàn là \({12^0}\) thì phi công phải bắt đầu hạ cánh từ vị trí cách sân bay bao xa? ( làm tròn kết quả đến một chữ số phần thập phân)
-
A.
\(56,6\,km\)
-
B.
\(56,5\,km\)
-
C.
\(55,6\,km\)
-
D.
\(57\,km\)
Tìm giá trị nhỏ nhất của biểu thức \(A = \sqrt {{m^2} + 2m + 1} + \sqrt {{m^2} - 8m + 16} \).
-
A.
$2$
-
B.
$9$
-
C.
$5$
-
D.
$10$
Lời giải và đáp án
Cho $\alpha $ và $\beta $ là hai góc nhọn bất kỳ thỏa mãn $\alpha + \beta = 90^\circ $. Khẳng định nào sau đây là đúng ?
-
A.
$\tan \alpha = \sin \beta $
-
B.
$\tan \alpha = \cot \beta $
-
C.
$\tan \alpha = \cos \alpha $
-
D.
$\tan \alpha = \tan \beta $
Đáp án : B
Với hai góc \(\alpha ,\beta \) mà \(\alpha + \beta = {90^0}\).
Ta có: \(\sin \alpha = \cos \beta ;\cos \alpha = \sin \beta ;\)
\(\tan \alpha = \cot \beta ;\cot \alpha = \tan \beta \).
Cho số thực \(a > 0\). Căn bậc hai số học của \(a\) là \(x\) khi và chỉ khi
-
A.
\(x = \sqrt a \)
-
B.
\(\sqrt x = a\)
-
C.
\({a^2} = x\,\) và \(x \ge 0\)
-
D.
\({x^2} = a\,\) và \(x \ge 0\)
Đáp án : D
Sử dụng kiến thức về căn bậc hai số học, lưu ý rằng căn hậc hai số học của một số không âm luôn là một số không âm.
Với số dương \(a\), số \(x\) được gọi là căn bậc hai số học của \(a\) khi và chỉ khi \(\sqrt a = x\) hay \( \left\{ \begin{array}{l}x \ge 0\\{x^2} = a\end{array} \right.\)
Khẳng định nào sau đây là đúng?
-
A.
$\sqrt[3]{a} = x$ nếu x = ${a^3}$
-
B.
$\sqrt[3]{a} = - x $ nếu $ - x= {a^3} $
-
C.
$\sqrt[3]{a} = x $ nếu ${x^3} = a$
-
D.
$\sqrt[3]{a} = - x$ nếu ${x^3} = a$
Đáp án : C
Dựa vào khái niệm căn bậc ba của số thực.
Căn bậc ba của một số thực a là số thực x thỏa mãn \(x^3 = a\) hay \(\sqrt[3]{a} = x\) thỏa mãn \(x^3 = a\).
Tính $x$ trong hình vẽ sau (làm tròn đến chữ số thập phân thứ hai)

-
A.
$x \approx 8,81$
-
B.
$x \approx 8,82$
-
C.
$x \approx 8,83$
-
D.
$x \approx 8,80$
Đáp án : B
Tính $x$ theo hệ thức lượng $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
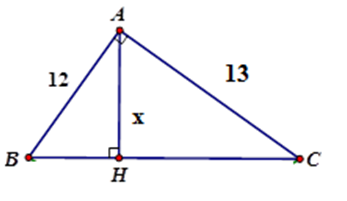
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông $ABC$ ta có:
$\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}$
\( \Leftrightarrow \dfrac{1}{{A{H^2}}} = \dfrac{{A{B^2} + A{C^2}}}{{A{B^2}.A{C^2}}} \)\(\Leftrightarrow A{H^2} = \dfrac{{A{B^2}.A{C^2}}}{{A{B^2} + A{C^2} }}\)
$ \Rightarrow AH = \dfrac{{AB.AC}}{{\sqrt {A{B^2} + A{C^2}} }} = \dfrac{{12.13}}{{\sqrt {{{12}^2} + {{13}^2}} }} \approx 8,82$
Vậy $x \approx 8,82$ .
Kết quả của phép tính $\sqrt {\dfrac{{81}}{{169}}} $ là?
-
A.
$\dfrac{9}{{13}}$
-
B.
$\dfrac{9}{{169}}$
-
C.
$\dfrac{3}{{13}}$
-
D.
$\dfrac{{13}}{9}$
Đáp án : A
Sử dụng công thức khai phương một thương: Với số $a$ không âm và số $b$ dương , ta có $\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}$.
$\sqrt {\dfrac{{81}}{{169}}} = \dfrac{{\sqrt {81} }}{{\sqrt {169} }} = \dfrac{{\sqrt {{9^2}} }}{{\sqrt {{{13}^2}} }} = \dfrac{9}{{13}}$
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là đúng ?

-
A.
$A{H^2} = AB.AC$
-
B.
$A{H^2} = BH.CH$
-
C.
$A{H^2} = AB.BH$
-
D.
$A{H^2} = CH.BC$
Đáp án : B
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ . Khi đó ta có hệ thức $H{A^2} = HB.HC$
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 9\,cm,\,\,AC = 5cm.\) Tính tỉ số lượng giác \(\tan C\) (làm tròn đến chữ số thập phân thứ \(1\) )
-
A.
\(\tan C \approx 0,67\)
-
B.
\(\tan C \approx 0,5\)
-
C.
\(\tan C \approx 1,4\)
-
D.
\(\tan C \approx 1,5\)
Đáp án : D
Bước 1: Tính cạnh còn lại theo định lý Pytago
Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn
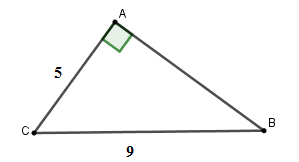
Theo định lý Py-ta-go ta có: \(B{C^2} = A{C^2} + A{B^2} \Rightarrow AB = \sqrt {{9^2} - {5^2}} = 2\sqrt {14} \)
Xét tam giác \(ABC\) vuông tại \(C\) có \(\tan C = \dfrac{{AB}}{{AC}} = \dfrac{{2\sqrt {14} }}{5} \approx 1,5\)
Một cầu trượt trong công viên có độ dốc là ${28^0}$ và có độ cao là $2,1m.$Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ hai).
-
A.
$3,95\,m$
-
B.
$3,8\,m$
-
C.
$4,5\,m$
-
D.
$4,47\,m$
Đáp án : D
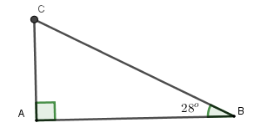
Ta có độ dài của mặt cầu trượt là $AB$; $AC = 2,1\,m$ và $\widehat {ABC} = 28^\circ $
Xét tam giác $ACB$ vuông tại $A$ có
$BC = AB:\sin B = 2,1:\sin 28^\circ \simeq 4,47\,m$
Vậy độ dài của mặt cầu trượt là $4,47\,m.$
So sánh hai số \(5\) và \(\sqrt {50} - 2\).
-
A.
\(5 > \sqrt {50} - 2\)
-
B.
\(5 = \sqrt {50} - 2\)
-
C.
\(5 < \sqrt {50} - 2\)
-
D.
Chưa đủ điều kiện để so sánh.
Đáp án : C
So sánh hai căn bậc hai: Với hai số \(a,b\) không âm ta có \(a < b \Leftrightarrow \sqrt a < \sqrt b \).
Tách \(5 = 7 - 2 = \sqrt {49} - 2\).
Vì \(49 < 50 \) nên \( \sqrt {49} < \sqrt {50} \)
\( 7 < \sqrt {50} \)
\(7 - 2 < \sqrt {50} - 2 \)
\( 5 < \sqrt {50} - 2\).
Đưa thừa số $5y\sqrt y $ ($y \ge 0$) vào trong dấu căn ta được
-
A.
$\sqrt {5{y^2}} $
-
B.
$\sqrt {25{y^3}} $
-
C.
$\sqrt {5{y^3}} $
-
D.
$\sqrt {25y\sqrt y } $
Đáp án : B
Đưa thừa số vào trong dấu căn
+) $A\sqrt B = \sqrt {{A^2}B} $ với $A \ge 0$ và $B \ge 0$
+) $A\sqrt B = - \sqrt {{A^2}B} $ với $A < 0$ và $B \ge 0$
Ta có $5y\sqrt y $$ = \sqrt {{{\left( {5y} \right)}^2}y} = \sqrt {25{y^2}.y} = \sqrt {25{y^3}} $.
Phép tính $\sqrt {{{\left( { - 5} \right)}^2}{{.7}^2}} $ có kết quả là?
-
A.
$35$
-
B.
$5$
-
C.
$ - 35$
-
D.
Không tồn tại.
Đáp án : A
-Sử dụng công thức khai phương một tích: Với hai số $a,b$ không âm, ta có $\sqrt a .\sqrt b = \sqrt {ab} $
-Sử dụng hằng đẳng thức $\sqrt {{A^2}} = \left| A \right|$
Cách giải:
$\sqrt {{{\left( { - 5} \right)}^2}{{.7}^2}} = \sqrt {{{\left( { - 5} \right)}^2}} .\sqrt {{7^2}} = \left| { - 5} \right|.\left| 7 \right| = 5.7 = 35$.
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.
-
A.
$\sin \alpha + \cos \alpha = 1$
-
B.
${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
-
C.
${\sin ^3}\alpha + {\cos ^3}\alpha = 1$
-
D.
$\sin \alpha - cos\alpha = 1$
Đáp án : B
Từ tỉ số lượng giác sin, cos để chứng minh.
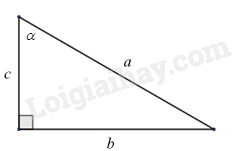
Giả sử ta có tam giác vuông có các cạnh và góc $\alpha $ như hình vẽ.
Áp dụng tỉ số lượng giác của góc nhọn, ta có:
$\sin \alpha =\frac{b}{a},\cos \alpha =\frac{c}{a},\tan \alpha =\frac{b}{c},\cot \alpha =\frac{c}{b}$.
Ta có: ${{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha ={{\left( \frac{b}{a} \right)}^{2}}+{{\left( \frac{c}{a} \right)}^{2}}=\frac{{{b}^{2}}+{{c}^{2}}}{{{a}^{2}}}=\frac{{{a}^{2}}}{{{a}^{2}}}=1$
Vậy ${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
Cho $a$ là số không âm, $b$ là số dương. Khẳng định nào sau đây là đúng?
-
A.
$\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{b}$
-
B.
$\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}$
-
C.
$\sqrt {\dfrac{a}{b}}=\dfrac{{ - \sqrt a }}{{\sqrt b }}$
-
D.
$\sqrt {\dfrac{a}{b}}=\dfrac{a}{{\sqrt b }}$
Đáp án : B
Sử dụng kiến thức căn thức bậc hai của một thương.
Với số $a$ không âm và số $b$ dương , ta có $\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}$.
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 15\,cm,\widehat B = 55^\circ .\) Tính \(AC;\widehat C\) . (làm tròn đến chữ số thập phân thứ hai)
-
A.
\(AC \approx 12,29;\widehat C = 45^\circ \)
-
B.
\(AC \approx 12,29;\widehat C = 35^\circ \)
-
C.
\(AC \approx 12,2;\widehat C = 35^\circ \)
-
D.
\(AC \approx 12,92;\widehat C = 40^\circ \)
Đáp án : B
+Tính góc còn lại theo định lý về tổng ba góc trong tam giác
+) Sử dụng hệ thức về cạnh và góc trong tam giác vuông để tìm các cạnh .
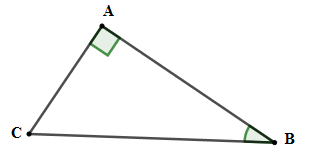
Xét tam giác \(ABC\) vuông tại \(A\) có
+) \(\sin B = \dfrac{{AC}}{{BC}} \Rightarrow AC = BC.\sin B = 15.\sin 55^\circ \approx 12,29\)
+) \(\widehat A + \widehat B + \widehat C = 180^\circ \Rightarrow \widehat C = 180^\circ - 55^\circ - 90^\circ = 35^\circ \)
Vậy \(AC \approx 12,29;\widehat C = 35^\circ \).
Tính \(x,y\) trong hình vẽ sau:

-
A.
\(x = 6,5;y = 9,5\)
-
B.
\(x = 6,25;y = 9,75\)
-
C.
\(x = 9,25;y = 6,75\)
-
D.
\(x = 6;y = 10\)
Đáp án : B
Tính \(x\) theo hệ thức lượng \(A{B^2} = BH.BC\) từ đó suy ra \(y\).
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
\(A{B^2} = BH.BC \Leftrightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{100}}{{16}} = 6,25\) \( \Rightarrow CH = BC - BH = 16 - 6,25 = 9,75\)
Vậy \(x = 6,25;y = 9,75\)
Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 1\,cm,\,\,BC = 2\,cm.\) Tính các tỉ số lượng giác \(\sin B;\cos B\)
-
A.
\(\sin B = \dfrac{1}{{\sqrt 3 }};\cos B = \dfrac{{2\sqrt 3 }}{3}\)
-
B.
\(\sin B = \dfrac{{\sqrt 5 }}{5};\cos B = \dfrac{{2\sqrt 5 }}{5}\)
-
C.
\(\sin B = \dfrac{1}{2};\cos B = \dfrac{2}{{\sqrt 5 }}\)
-
D.
\(\sin B = \dfrac{{2\sqrt 5 }}{5};\cos B = \dfrac{{\sqrt 5 }}{5}\)
Đáp án : B
Bước 1: Tính cạnh còn lại theo định lý Pytago
Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn
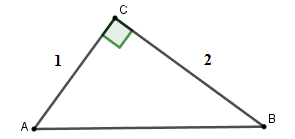
Theo định lý Py-ta-go ta có: \(A{B^2} = A{C^2} + B{C^2} \Rightarrow AB = \sqrt {{1^2} + {2^2}} = \sqrt 5 \)
Xét tam giác \(ABC\) vuông tại \(C\) có \(\sin B = \dfrac{{AC}}{{AB}} = \dfrac{1}{{\sqrt 5 }} = \dfrac{{\sqrt 5 }}{5}\) và \(\cos B = \dfrac{{BC}}{{AB}} = \dfrac{2}{{\sqrt 5 }} = \dfrac{{2\sqrt 5 }}{5}\)
Tính giá trị biểu thức \(\sqrt {19 + 8\sqrt 3 } + \sqrt {19 - 8\sqrt 3 } \).
-
A.
\(2\sqrt 3 \)
-
B.
\(8 + 2\sqrt 3 \)
-
C.
\(6\)
-
D.
\(8\)
Đáp án : D
- Đưa biểu thức dưới dấu căn thành hằng đẳng thức \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\) và \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\).
- Sử dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\)
- Phá dấu giá trị tuyệt đối \(\left| A \right| = \left\{ \begin{array}{l}A\,\,khi\,A \ge 0\\ - A\,\,\,khi\,A < 0\end{array} \right.\).
Ta có: \(\sqrt {19 + 8\sqrt 3 } = \sqrt {{4^2} + 2.4.\sqrt 3 + 3} = \sqrt {{{\left( {4 + \sqrt 3 } \right)}^2}} = \left| {4 + \sqrt 3 } \right| = 4 + \sqrt 3 \)
Và \(\sqrt {19 - 8\sqrt 3 } = \sqrt {{4^2} - 2.4.\sqrt 3 + 3} = \sqrt {{{\left( {4 - \sqrt 3 } \right)}^2}} = \left| {4 - \sqrt 3 } \right| = 4 - \sqrt 3 \) (vì \(4 = \sqrt {16} > \sqrt 3 \Rightarrow 4 - \sqrt 3 > 0\))
Nên \(\sqrt {19 + 8\sqrt 3 } + \sqrt {19 - 8\sqrt 3 } \)\( = 4 + \sqrt 3 + 4 - \sqrt 3 = 8\)
Giá trị biểu thức \(\sqrt {5x + 3} .\sqrt {5x - 3} \) khi \(x = \sqrt {3,6} \) là:
-
A.
\(3,6\)
-
B.
\(3\)
-
C.
\(81\)
-
D.
\(9\)
Đáp án : D
- Sử dụng công thức khai phương một tích: Với hai số \(a,b\) không âm, ta có \(\sqrt a .\sqrt b = \sqrt {ab} \)
Ta có: \(\sqrt {\left( {5x - 3} \right)\left( {5x + 3} \right)} = \sqrt {25{x^2} - 9} \) với \(x \ge \dfrac{3}{5}\)
Thay \(x = \sqrt {3,6} \) (tm đk \(x \ge \dfrac{3}{5}\)) vào biểu thức ta được: \(\sqrt {25{x^2} - 9} = \sqrt {25.{{\left( {\sqrt {3,6} } \right)}^2} - 9} = \sqrt {81} = 9\).
Rút gọn biểu thức $4{a^4}{b^2}.\sqrt {\dfrac{9}{{{a^8}{b^4}}}} $ với $ab \ne 0$ ta được
-
A.
$\dfrac{{{a^2}}}{b}$
-
B.
$12$
-
C.
$6$
-
D.
$36$
Đáp án : B
+ Sử dụng công thức khai phương một thương: Với số $a$ không âm và số $b$ dương, ta có $\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}$.
+ Sử dụng hằng đẳng thức $\sqrt {{A^2}} = \left| A \right|$
Ta có $4{a^4}{b^2}.\sqrt {\dfrac{9}{{{a^8}{b^4}}}} $$ = 4{a^4}{b^2}.\dfrac{{\sqrt 9 }}{{\sqrt {{a^8}{b^4}} }} = 4{a^4}{b^2}.\dfrac{3}{{\sqrt {{a^8}} .\sqrt {{b^4}} }}$$ = \dfrac{{12{a^4}{b^2}}}{{\sqrt {{{\left( {{a^4}} \right)}^2}} .\sqrt {{{\left( {{b^2}} \right)}^2}} }} = \dfrac{{12{a^4}{b^2}}}{{{a^4}.{b^2}}} = 12$.
Rút gọn biểu thức \(\dfrac{a}{{\sqrt 5 + 1}} + \dfrac{a}{{\sqrt 5 - 2}} - \dfrac{a}{{3 - \sqrt 5 }} - \sqrt 5 a\) ta được
-
A.
$2a$
-
B.
$a$
-
C.
$3a$
-
D.
$12a$
Đáp án : B
-Trục căn thức ở mẫu theo công thức
Với các biểu thức $A,B,C$ mà $A \ge 0,A \ne {B^2}$, ta có $\dfrac{C}{{\sqrt A + B}} = \dfrac{{C\left( {\sqrt A - B} \right)}}{{A - {B^2}}};\dfrac{C}{{\sqrt A - B}} = \dfrac{{C\left( {\sqrt A + B} \right)}}{{A - {B^2}}}$
-Quy đồng mẫu số các phân số rồi rút gọn
Ta có \(\dfrac{a}{{\sqrt 5 + 1}} + \dfrac{a}{{\sqrt 5 - 2}} - \dfrac{a}{{3 - \sqrt 5 }} - \sqrt 5 a\)$ = \dfrac{{a\left( {\sqrt 5 - 1} \right)}}{{\left( {\sqrt 5 - 1} \right)\left( {\sqrt 5 + 1} \right)}} + \dfrac{{a\left( {\sqrt 5 + 2} \right)}}{{\left( {\sqrt 5 - 2} \right)\left( {\sqrt 5 + 2} \right)}} - \dfrac{{a\left( {3 + \sqrt 5 } \right)}}{{\left( {3 + \sqrt 5 } \right)\left( {3 - \sqrt 5 } \right)}} - \sqrt 5 a$
$ = \dfrac{{a\left( {\sqrt 5 - 1} \right)}}{4} + \dfrac{{a\left( {\sqrt 5 + 2} \right)}}{1} - \dfrac{{a\left( {3 + \sqrt 5 } \right)}}{4} - \sqrt 5 a$$ = \dfrac{{a\left( {\sqrt 5 - 1} \right) + 4a\left( {2 + \sqrt 5 } \right) - a\left( {3 + \sqrt 5 } \right) - 4\sqrt 5 a}}{4}$
$ = \dfrac{{a\left( {\sqrt 5 - 1 + 8+ 4\sqrt 5 - 3 - \sqrt 5 - 4\sqrt 5 } \right)}}{4} = \dfrac{{4a}}{4} = a$
Rút gọn biểu thức \(5\sqrt a - 4b\sqrt {25{a^3}} + 5a\sqrt {16a{b^2}} - \sqrt {9a} \) với $a \ge 0;b \ge 0$ ta được kết quả là
-
A.
$2\sqrt {2a} $
-
B.
$4\sqrt a $
-
C.
$8\sqrt a $
-
D.
$2\sqrt a $
Đáp án : D
Sử dụng công thức đưa thừa số vào trong dấu căn và công thức khai phương một tích để xuất hiện nhân tử chung từ đó thực hiện phép tính.
Đưa thừa số vào trong dấu căn
+) $A\sqrt B = \sqrt {{A^2}B} $ với $A \ge 0$ và $B \ge 0$
+) $A\sqrt B = - \sqrt {{A^2}B} $ với $A < 0$ và $B \ge 0$
Công thức khai phương một tích
$\sqrt {AB} = \sqrt A .\sqrt B \,\,\left( {A \ge 0;B \ge 0} \right)$
Ta có \(5\sqrt a - 4b\sqrt {25{a^3}} + 5a\sqrt {16a{b^2}} - \sqrt {9a} \)$ = 5\sqrt a - 4\sqrt {25{a^3}{b^2}} + 5\sqrt {16a{b^2}.{a^2}} - \sqrt 9 .\sqrt a $
$ = 5\sqrt a - 4\sqrt {25} .\sqrt {{a^3}{b^2}} + 5\sqrt {16} .\sqrt {{a^3}{b^2}} - 3\sqrt a $$ = \left( {5\sqrt a - 3\sqrt a } \right) - \left( {4.5\sqrt {{a^3}{b^2}} - 5.4\sqrt {{a^3}{b^2}} } \right)$$ = 2\sqrt a $
Cho $P = \dfrac{2}{{\sqrt x + 1}}$ .
Có bao nhiêu giá trị $x \in \mathbb{Z}$ để $P \in \mathbb{Z}$ ?
-
A.
$1$
-
B.
$2$
-
C.
$0$
-
D.
$4$
Đáp án : B
Sử dụng: với $P = \dfrac{a}{b}$ với $a,b \in \mathbb{Z}$ thì $P \in \mathbb{Z}$ khi $ a \vdots b$
Ta có để $P = \dfrac{2}{{\sqrt x + 1}}$ thì $2 \vdots \left( {\sqrt x + 1} \right)$ $ \left( {\sqrt x + 1} \right) \in $Ư$\left( 2 \right) = \left\{ {1; - 1;2; - 2} \right\}$
Mà $\sqrt x + 1 > 0$ với $x \ge 0$ nên $\sqrt x + 1 \in \left\{ {1;2} \right\}$
+) $\sqrt x + 1 = 1 $ hay $ x = 0$ (TM )
+) $\sqrt x + 1 = 2 $ hay $ x = 1$ (TM )
Vậy có hai giá trị của $x$ thỏa mãn điều kiện.
Rút gọn biểu thức \(2\sqrt a - \sqrt {9{a^3}} + {a^2}\sqrt {\dfrac{{16}}{a}} + \dfrac{2}{{{a^2}}}\sqrt {36{a^5}} \) với $a > 0$ ta được
-
A.
$14\sqrt a + a\sqrt a $
-
B.
$14\sqrt a - a\sqrt a $
-
C.
$14\sqrt a + 2a\sqrt a $
-
D.
$20\sqrt a - 2a\sqrt a $
Đáp án : A
-Sử dụng công thức khai phương một thương \(\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt A }}{{\sqrt B }}\) với \(A \ge 0,B > 0\) và công thức khai phương một tích \(\sqrt {AB} = \sqrt A .\sqrt B ,\,\,\left( {A,B \ge 0} \right)\)
-Khử mẫu biểu thức lấy căn theo công thức \(\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt {AB} }}{B}\,\left( {A \ge 0,B > 0} \right)\)
-Sử dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\)
-Cộng trừ các căn thức bậc hai.
Với $a>0$ ta có \(2\sqrt a - \sqrt {9{a^3}} + {a^2}\sqrt {\dfrac{{16}}{a}} + \dfrac{2}{{{a^2}}}\sqrt {36{a^5}} \)$ = 2\sqrt a - \sqrt {9{a^2}.a} + {a^2}\dfrac{{\sqrt {16a} }}{a} + \dfrac{2}{{{a^2}}}.\sqrt {36{a^4}.a} $
$ = 2\sqrt a - 3a\sqrt a + 4a\sqrt a + \dfrac{2}{{{a^2}}}.6{a^2}\sqrt a $$ = 2\sqrt a - 3a\sqrt a + 4a\sqrt a + 12\sqrt a = 14\sqrt a + a\sqrt a $
Thu gọn biểu thức \(\dfrac{{\sqrt[3]{{ - 64{a^5}{b^5}}}}}{{\sqrt[3]{{{a^2}{b^2}}}}}\) ta được:
-
A.
\(4ab\)
-
B.
\( - 8ab\)
-
C.
\(16ab\)
-
D.
\( - 4ab\)
Đáp án : D
- Áp dụng \(\dfrac{{\sqrt[3]{a}}}{{\sqrt[3]{b}}} = \sqrt[3]{{\dfrac{a}{b}}}\) và \(\sqrt[3]{{{a^3}}} = a\).
Ta có: \(\dfrac{{\sqrt[3]{{ - 64{a^5}{b^5}}}}}{{\sqrt[3]{{{a^2}{b^2}}}}}\)\( = \sqrt[3]{{\dfrac{{ - 64{a^5}{b^5}}}{{{a^2}{b^2}}}}} = \sqrt[3]{{ - 64{a^3}{b^3}}} = \sqrt[3]{{{{\left( { - 4ab} \right)}^3}}} = - 4ab\).
Tính \(x,y\) trong hình vẽ sau:

-
A.
\(x = 3,2;y = 1,8\)
-
B.
\(x = 1,8;y = 3,2\)
-
C.
\(x = 2;y = 3\)
-
D.
\(x = 3;y = 2\)
Đáp án : B
Bước 1: Tính \(BC\) theo định lý Pytago
Bước 2: Tính \(x,y\) theo hệ thức lượng \(A{B^2} = BH.BC;A{C^2} = CH.BC\)
Theo định lý Pytago ta có \(B{C^2} = A{B^2} + A{C^2} \Leftrightarrow B{C^2} = 25 \Leftrightarrow BC = 5\)
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
\(A{B^2} = BH.BC \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{3^2}}}{5} = 1,8\) hay \(x = 1,8\)
\( \Rightarrow CH = BC - BH = 5 - 1,8 = 3,2\) hay \(y = 3,2\).
Vậy \(x = 1,8;y = 3,2\)
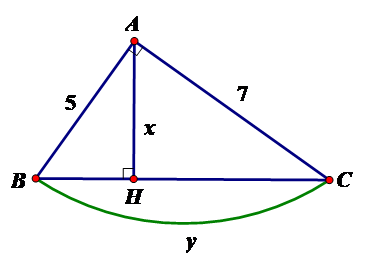
Tính $x,y$ trong hình vẽ sau:

-
A.
$x = \dfrac{{35\sqrt {74} }}{{74}};y = \sqrt {74} $
-
B.
$y = \dfrac{{35\sqrt {74} }}{{74}};x= \sqrt {74} $
-
C.
$x = 4;y = 6$
-
D.
$x = 2,8;y = 7,2$
Đáp án : A
Bước 1: Tính $BC$ theo định lý Pytago
Bước 2: Tính $x,y$ theo hệ thức lượng $AH.BC = AB.AC$
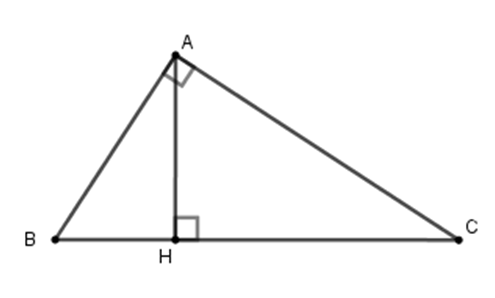
Theo định lý Pytago ta có $B{C^2} = A{B^2} + A{C^2} \Leftrightarrow B{C^2} = 74 \Leftrightarrow BC = \sqrt {74} $
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
$AH.BC = AB.AC \Leftrightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{5.7}}{{\sqrt {74} }} = \dfrac{{35\sqrt {74} }}{{74}}$
Vậy $x = \dfrac{{35\sqrt {74} }}{{74}};y = \sqrt {74} $
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(AB = 13\,cm,\,BH = 0,5\,dm\) Tính tỉ số lượng giác $\sin C$ (làm tròn đến chữ số thập phân thứ $2$ )
-
A.
$\sin C \approx 0,35$
-
B.
$\sin C \approx 0,37$
-
C.
$\sin C \approx 0,39$
-
D.
$\sin C \approx 0,38$
Đáp án : D
Bước 1: Tính cạnh cần thiết lại theo định lý Pytago hoặc hệ thức lượng trong tam giác vuông.
Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn
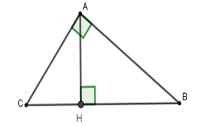
Đổi $0,5\,dm = 5\,cm$
Xét tam giác $ABC$ vuông tại $A$,
theo hệ thức lượng trong tam giác vuông ta có
$A{B^2} = BH.BC \Rightarrow BC = \dfrac{{A{B^2}}}{{BH}} = \dfrac{{{{13}^2}}}{5} = 33,8\,\,cm$
$ \Rightarrow \sin C = \dfrac{{AB}}{{BC}}$
$= \dfrac{{13}}{{33,8}} \approx 0,38$
Tính giá trị biểu thức \(B = \tan 10^\circ .\tan 20^\circ .\tan 30^\circ .....tan80^\circ \)
-
A.
\(B = 44\)
-
B.
\(B = 1\)
-
C.
\(B = 45\)
-
D.
\(B = 2\)
Đáp án : B
Bước 1 : Đưa các tỉ số lượng giác về cùng một góc hoặc cùng loại (sử dụng tính chất "Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia")
Bước 2 : Sử dụng đẳng thức lượng giác \(\tan \alpha .\cot\alpha = 1\).
Ta có \(\tan 80^\circ = cot10^\circ ;\tan 70^\circ = cot20^\circ ;\tan 50^\circ = cot40^\circ ;\tan 60^\circ = \cot 30^\circ \) và \(\tan \alpha .cot\alpha = 1\)
Nên \(B = \tan 10^\circ .\tan 20^\circ .\tan 30^\circ .\tan 40^\circ .\tan 50^\circ .\tan 60^\circ .\tan 70^\circ .tan80^\circ \)\( = \tan 10^\circ .\tan 20^\circ .\tan 30^\circ .\tan 40^\circ .\cot 40^\circ .\cot 30^\circ .\cot 20^\circ .\cot 10^\circ \)
\( = \left( {\tan 10^\circ .\cot 10^\circ } \right).\left( {\tan 20^\circ .\cot 20^\circ } \right).\left( {\tan 30^\circ .\cot 30^\circ } \right).\left( {\tan 40^\circ .\cot 40^\circ } \right)\)
\( = 1.1.1.1 = 1\)
Vậy \(B = 1\).
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 7\,cm,AB = \,5cm\). Tính $BC;\widehat C$ .
-
A.
$BC = \sqrt {74} (cm);\widehat C \approx 35^\circ 32'$
-
B.
$BC = \sqrt {74} (cm);\widehat C \approx 36^\circ 32'$
-
C.
$BC = \sqrt {74} (cm) ;\widehat C \approx 35^\circ 33'$
-
D.
$BC = \sqrt {75} (cm) ;\widehat C \approx 35^\circ 32'$
Đáp án : A
+) Tính cạnh còn lại theo định lý Py-ta-go
+) Tìm tỉ số lượng giác của góc từ đó suy ra góc.
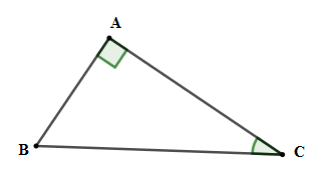
Xét tam giác \(ABC\) vuông tại \(A\) có
+) $B{C^2} = A{B^2} + A{C^2} = {5^2} + {7^2} = 74 \Rightarrow BC = \sqrt {74} (cm)$
+) $\tan C = \dfrac{{AB}}{{AC}} = \dfrac{5}{7} \Rightarrow \widehat C \approx 35^\circ 32'$
Vậy $BC = \sqrt {74}(cm) ;\widehat C \approx 35^\circ 32'$.
Cho tam giác \(ABC\) có \(AB = 16,AC = 14\) và \(\widehat B = {60^0}\). Tính $BC$
-
A.
$BC = 10$
-
B.
$BC = 11$
-
C.
$BC = 9$
-
D.
$BC = 12$
Đáp án : A
+) Kẻ đường cao $AH$
+) Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông thích hợp và định lý Py-ta-go để tính cạnh.
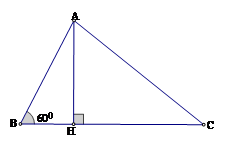
Kẻ đường cao \(AH\).
Xét tam giác vuông \(ABH\), ta có: \(BH = AB.\cos B = AB.\cos {60^0} = 16.\dfrac{1}{2} = 8\)\(AH = AB.\sin B = AB.\sin {60^0} = 16.\dfrac{{\sqrt 3 }}{2} = 8\sqrt 3 \).
Áp dụng định lý Pythago vào tam giác vuông \(AHC\) ta có:
\(H{C^2} = A{C^2} - A{H^2} = {14^2} - {\left( {8\sqrt 3 } \right)^2} = 196 - 192 = 4\). Suy ra \(HC = 2\). Vậy \(BC = CH + HB = 2 + 8 = 10\).
Một máy bay đang bay ở độ cao \(12km\) so với mặt đất, muốn hạ cánh xuống sân bay. Để đường bay và mặt đất hợp thành một góc an toàn là \({12^0}\) thì phi công phải bắt đầu hạ cánh từ vị trí cách sân bay bao xa? ( làm tròn kết quả đến một chữ số phần thập phân)
-
A.
\(56,6\,km\)
-
B.
\(56,5\,km\)
-
C.
\(55,6\,km\)
-
D.
\(57\,km\)
Đáp án : B
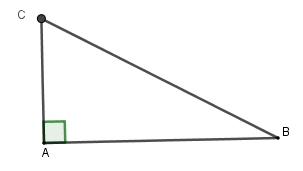
Từ giả thiết suy ra \(AC = 12\,\,km;\,\,\widehat B = 12^\circ \).
Xét tam giác \(\Delta ABC\) vuông tại \(A\) có \(AB = AC.\cot B = 12.\cot 12^\circ \simeq 56,5\,km\)
Tìm giá trị nhỏ nhất của biểu thức \(A = \sqrt {{m^2} + 2m + 1} + \sqrt {{m^2} - 8m + 16} \).
-
A.
$2$
-
B.
$9$
-
C.
$5$
-
D.
$10$
Đáp án : C
- Đưa biểu thức dưới dấu căn thành hằng đẳng thức.
- Sử dụng hằng đẳng thức $\sqrt {{A^2}} = \left| A \right|$
- Sử dụng bất đẳng thức \(\left| A \right| + \left| B \right| \ge \left| {A + B} \right|\) với mọi \(A,B.\) Dấu ‘=’ xảy ra \( \Leftrightarrow A = B\)
Ta có \(A = \sqrt {{m^2} + 2m + 1} + \sqrt {{m^2} - 8m + 16} \)\( = \sqrt {{{\left( {m + 1} \right)}^2}} + \sqrt {{{\left( {m - 4} \right)}^2}} = \left| {m + 1} \right| + \left| {m - 4} \right|\)
Ta có \(\left| {m + 1} \right| + \left| {m - 4} \right| = \left| {m + 1} \right| + \left| {4 - m} \right| \ge \left| {m + 1 + 4 - m} \right| = 5\)
Dấu “=” xảy ra khi \(m + 1 = 4 - m \) hay \( 2m = 3 \Leftrightarrow m = \dfrac{3}{2}\)
Suy ra GTNN của \(B\) là \(5 \) khi \( m = \dfrac{3}{2}\) .